MATLAB - बहुपद
MATLAB बहुपत्नी शक्तियों के रूप में आदेशित गुणांक वाले पंक्ति वैक्टर के रूप में बहुपद का प्रतिनिधित्व करता है। उदाहरण के लिए, समीकरण P (x) = x 4 + 7x 3 - 5x + 9 को इस रूप में दर्शाया जा सकता है -
पी = [1 7 0 -5 -5];
बहुपद का मूल्यांकन
polyvalफ़ंक्शन का उपयोग एक निर्दिष्ट मूल्य पर एक बहुपद का मूल्यांकन करने के लिए किया जाता है। उदाहरण के लिए, हमारे पिछले बहुपद का मूल्यांकन करने के लिएp, x = 4 पर, टाइप करें -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB उपरोक्त कथनों को निष्पादित करता है और निम्नलिखित परिणाम देता है -
ans = 693MATLAB भी प्रदान करता है polyvalmएक मैट्रिक्स बहुपद का मूल्यांकन करने के लिए कार्य करता है। एक मैट्रिक्स बहुपद एक हैpolynomial चर के रूप में मैट्रिसेस के साथ।
उदाहरण के लिए, आइए हम एक वर्ग मैट्रिक्स X बनाएँ और X पर बहुपद p का मूल्यांकन करें।
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB उपरोक्त कथनों को निष्पादित करता है और निम्नलिखित परिणाम देता है -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269बहुपद की जड़ें खोजना
rootsफ़ंक्शन एक बहुपद की जड़ों की गणना करता है। उदाहरण के लिए, हमारे बहुपद p की जड़ों की गणना करने के लिए, -
p = [1 7 0 -5 9];
r = roots(p)MATLAB उपरोक्त कथनों को निष्पादित करता है और निम्नलिखित परिणाम देता है -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iकार्यक्रम polyजड़ों के कार्य का विलोम है और बहुपद गुणांक पर लौटता है। उदाहरण के लिए -
p2 = poly(r)MATLAB उपरोक्त कथनों को निष्पादित करता है और निम्नलिखित परिणाम देता है -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iबहुपद वक्र फिटिंग
polyfitफ़ंक्शन एक बहुपद के गुणांक को पाता है जो कम से कम वर्गों में डेटा के एक सेट को फिट बैठता है। यदि x और y दो वैक्टर हैं जिसमें x और y डेटा को n-डिग्री बहुपद में फिट किया जाना है, तो हम बहुपद को लिखकर डेटा फिटिंग करते हैं -
p = polyfit(x,y,n)उदाहरण
एक स्क्रिप्ट फ़ाइल बनाएँ और निम्न कोड टाइप करें -
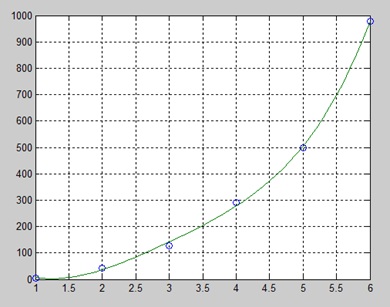
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onजब आप फ़ाइल चलाते हैं, तो MATLAB निम्न परिणाम प्रदर्शित करता है -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250और निम्नलिखित ग्राफ भूखंडों -