एक त्रिकोणीय प्रिज्म की सतह क्षेत्र को खोजने के लिए एक जाल का उपयोग करना
इस पाठ में, हम त्रिकोणीय प्रिज्म के सतह क्षेत्र को खोजने के लिए एक त्रिकोणीय प्रिज्म के जाल का उपयोग करते हैं।
net एक ठोस आकृति तब बनती है जब एक ठोस आकृति उसके किनारों के साथ सामने आती है और उसके चेहरे को दो आयामों में एक पैटर्न में रखा जाता है।
त्रिकोणीय प्रिज्म के जाल आयतों और त्रिभुजों से बने होते हैं।
Using a net to find the surface area of a rectangular prism
त्रिकोणीय प्रिज्म के जाल के आयतों और त्रिकोणों में से प्रत्येक के क्षेत्रों का पता लगाना और उन क्षेत्रों को जोड़ना त्रिकोणीय प्रिज्म का सतह क्षेत्र या कुल सतह क्षेत्र देता है।
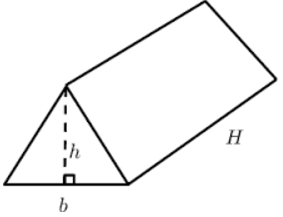
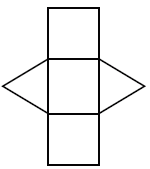
उदाहरण के लिए, एक समकोण त्रिभुज का आधार जो त्रिभुजाकार प्रिज्म का आधार है, 3 और 4 इकाइयाँ हैं और प्रिज़्म की ऊँचाई 10 इकाई है। नेट से, हम देख सकते हैं कि दो बधाई त्रिकोण चेहरे और तीन आयताकार चेहरे हैं जिनके क्षेत्र निम्नानुसार हैं। 6 वर्ग इकाइयाँ और (3 + 4 + 5) 10 = 120 वर्ग इकाइयाँ। प्रिज्म का सतही क्षेत्र = 2 (6) + 120 = 132 वर्ग इकाई।
Surface Area of a Triangular Prism using Nets
नेट का उपयोग करके निम्नलिखित त्रिकोणीय प्रिज्म की सतह क्षेत्र का पता लगाएं।

उपाय
Step 1:
त्रिकोणीय प्रिज्म के सतह क्षेत्र का उपयोग करना
त्रिभुज आधार के पक्ष
ए = 13 मिमी; बी = 13 मिमी; सी = 10 मिमी; ऊंचाई h = 14 मिमी
त्रिभुज क्षेत्र = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{18\left ( 18-13 \right )\left ( 18-13 \right )\left ( 18-10 \right )}$
= 60 वर्ग मिमी
Step 2:
प्रिज्म का भूतल क्षेत्र = 2 त्रिभुज क्षेत्र + h (a + b + c)
= 2 (60) + (13 + 13 + 10) 14
= 120 + 504
= 624 वर्ग सेमी
नेट का उपयोग करके निम्नलिखित त्रिकोणीय प्रिज्म की सतह क्षेत्र का पता लगाएं।

उपाय
Step 1:
त्रिकोणीय प्रिज्म के सतह क्षेत्र का उपयोग करना
त्रिभुज आधार के पक्ष
ए = 21 सेमी; बी = 28 सेमी; सी = 35 सेमी; ऊंचाई h = 14 सेमी
त्रिभुज क्षेत्र = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{42\left ( 42-21 \right )\left ( 42-28 \right )\left ( 42-35 \right )}$
= 294
Step 2:
प्रिज्म का भूतल क्षेत्र = 2 त्रिभुज क्षेत्र + h (a + b + c)
= 2 (294) + (21 + 28 + 35) 14
= 588 + 1176
= 1764 वर्ग सेमी