Volume Padatan terbuat dari Kubus dengan Panjang Tepi Pecahan Satuan

pengantar

Di sini kita menemukan volume padatan yang terbuat dari kubus dengan panjang tepi pecahan satuan. Pertimbangkan misalnya benda padat berukuran 3 in × 3 in × 3 terbuat dari kubus kecil dengan panjang tepi $ \ frac {1} {2} $ inci.

Dalam kasus ini, padatan terdiri dari 6 × 6 × 6 kubus kecil dengan panjang tepi $ \ frac {1} {2} $ inci. Jadi volume padatan dalam kasus ini adalah

Volume = lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $

= 3 × 3 × 3 = 27 inci kubik

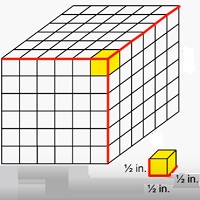
Rumus volume benda padat yang terbuat dari kubus dengan panjang tepi pecahan satuan

Mengasumsikan padatan menjadi kubus dari tepi a unit

b = jumlah kubus dengan panjang tepi pecahan satuan di setiap sisinya

k = satuan panjang tepi pecahan

Volume of solid = b × k × b × k × b × k cubic units

Contoh 1

Tentukan volume padatan berikut dari kubus dengan panjang tepi pecahan satuan. Setiap satuan prisma diukur dalam cm (bukan skala)

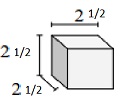
Larutan

Step 1:

Padat kubus dengan panjang tepi pecahan satuan $ \ frac {1} {2} $ cm

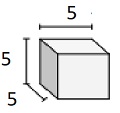
Step 2:

Volume V = lwh = $ 2 \ frac {1} {2} \ times 2 \ frac {1} {2} \ times 2 \ frac {1} {2} $

= $ 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} $

= $ 15 \ frac {5} {8} $ cu cm

Contoh 2

Tentukan volume padatan berikut dari kubus dengan panjang tepi pecahan satuan. Setiap satuan prisma diukur dalam cm (bukan skala)

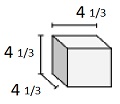
Larutan

Step 1:

Padat kubus dengan panjang tepi pecahan satuan $ \ frac {1} {3} $ cm

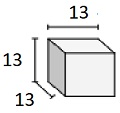
Step 2:

Volume V = lwh = $ 4 \ frac {1} {3} \ kali 4 \ frac {1} {3} \ times 4 \ frac {1} {3} $

= $ 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} $

= $ 81 \ frac {10} {27} $ cu cm