Teori Automata - Panduan Cepat
Automata - Apa itu?
Istilah "Automata" berasal dari kata Yunani "αὐτόματα" yang berarti "bertindak sendiri". Automaton (Automata dalam bentuk jamak) adalah perangkat komputasi self-propelled abstrak yang mengikuti urutan operasi yang telah ditentukan secara otomatis.
Sebuah robot dengan jumlah negara yang terbatas disebut a Finite Automaton (FA) atau Finite State Machine (FSM).
Definisi formal dari Finite Automaton
Sebuah robot dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F), di mana -
Q adalah sekumpulan negara yang terbatas.
∑ adalah kumpulan simbol yang terbatas, yang disebut alphabet dari robot tersebut.
δ adalah fungsi transisi.
q0adalah keadaan awal dari mana input diproses (q 0 ∈ Q).
F adalah himpunan keadaan akhir dari Q (F ⊆ Q).
Terminologi Terkait
Alfabet
Definition - An alphabet adalah kumpulan simbol yang terbatas.
Example - ∑ = {a, b, c, d} adalah sebuah alphabet set di mana 'a', 'b', 'c', dan 'd' berada symbols.
Tali
Definition - A string adalah urutan simbol berhingga yang diambil dari ∑.
Example - 'cabcad' adalah string yang valid pada kumpulan alfabet ∑ = {a, b, c, d}
Panjang String
Definition- Ini adalah jumlah simbol yang ada dalam sebuah string. (Dilambangkan dengan|S|).
Examples -
Jika S = 'cabcad', | S | = 6
Jika | S | = 0, maka disebut an empty string (Dilambangkan dengan λ atau ε)
Kleene Star
Definition - Bintang Kleene, ∑*, adalah operator unary pada satu set simbol atau string, ∑, yang memberikan himpunan tak terbatas dari semua kemungkinan string dengan semua panjang yang memungkinkan ∑ termasuk λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. di mana ∑ p adalah himpunan dari semua kemungkinan string dengan panjang p.
Example - Jika ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Penutupan Kleene / Plus
Definition - Set ∑+ adalah himpunan tak terhingga dari semua kemungkinan string dengan semua panjang yang mungkin di atas ∑ tidak termasuk λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Jika ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Bahasa
Definition- Bahasa adalah himpunan bagian dari ∑ * untuk beberapa alfabet ∑. Itu bisa terbatas atau tidak terbatas.
Example - Jika bahasa mengambil semua kemungkinan string dengan panjang 2 di atas ∑ = {a, b}, maka L = {ab, aa, ba, bb}
Hingga Automaton dapat diklasifikasikan menjadi dua jenis -
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NDFA / NFA)
Deterministic Finite Automaton (DFA)
Di DFA, untuk setiap simbol input, seseorang dapat menentukan status ke mana mesin akan bergerak. Karenanya, ini disebutDeterministic Automaton. Karena memiliki jumlah status yang terbatas, mesin dipanggilDeterministic Finite Machine atau Deterministic Finite Automaton.
Definisi Formal dari DFA
DFA dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F) di mana -
Q adalah sekumpulan negara yang terbatas.
∑ adalah seperangkat simbol terbatas yang disebut alfabet.
δ adalah fungsi transisi di mana δ: Q × ∑ → Q
q0adalah keadaan awal dari mana input diproses (q 0 ∈ Q).
F adalah himpunan keadaan akhir dari Q (F ⊆ Q).
Representasi Grafis DFA
DFA diwakili oleh digraf yang disebut state diagram.
- Simpul mewakili negara bagian.
- Busur yang diberi label alfabet masukan menunjukkan transisi.
- Keadaan awal dilambangkan dengan busur masuk tunggal yang kosong.
- Keadaan akhir ditunjukkan oleh lingkaran ganda.
Contoh
Biarkan robot deterministik hingga →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c}, dan
Fungsi transisi δ seperti yang ditunjukkan pada tabel berikut -
| Keadaan Sekarang | Status Berikutnya untuk Input 0 | Status Berikutnya untuk Input 1 |
|---|---|---|
| a | Sebuah | b |
| b | c | Sebuah |
| c | b | c |
Representasi grafisnya adalah sebagai berikut -

Di NDFA, untuk simbol input tertentu, mesin dapat berpindah ke kombinasi status apa pun di mesin. Dengan kata lain, keadaan pasti pergerakan mesin tidak dapat ditentukan. Karenanya, ini disebutNon-deterministic Automaton. Karena memiliki jumlah status yang terbatas, mesin dipanggilNon-deterministic Finite Machine atau Non-deterministic Finite Automaton.
Definisi Formal dari NDFA
Sebuah NDFA dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F) di mana -
Q adalah sekumpulan negara yang terbatas.
∑ adalah seperangkat simbol terbatas yang disebut huruf.
δadalah fungsi transisi di mana δ: Q × ∑ → 2 Q
(Di sini kumpulan daya Q (2 Q ) telah diambil karena dalam kasus NDFA, dari suatu keadaan, transisi dapat terjadi ke kombinasi keadaan Q apa pun)
q0adalah keadaan awal dari mana input diproses (q 0 ∈ Q).
F adalah himpunan keadaan akhir dari Q (F ⊆ Q).
Representasi Grafis NDFA: (sama seperti DFA)
NDFA diwakili oleh digraf yang disebut diagram keadaan.
- Simpul mewakili negara bagian.
- Busur yang diberi label alfabet masukan menunjukkan transisi.
- Keadaan awal dilambangkan dengan busur masuk tunggal yang kosong.
- Keadaan akhir ditunjukkan oleh lingkaran ganda.
Example
Biarkan robot terbatas non-deterministik menjadi →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
Fungsi transisi δ seperti yang ditunjukkan di bawah ini -
| Keadaan Sekarang | Status Berikutnya untuk Input 0 | Status Berikutnya untuk Input 1 |
|---|---|---|
| Sebuah | a, b | b |
| b | c | a, c |
| c | b, c | c |
Representasi grafisnya adalah sebagai berikut -
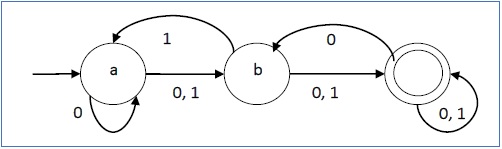
DFA vs NDFA
Tabel berikut mencantumkan perbedaan antara DFA dan NDFA.
| DFA | NDFA |
|---|---|
| Transisi dari suatu keadaan adalah ke keadaan tertentu berikutnya untuk setiap simbol masukan. Karena itu disebut deterministik . | Transisi dari suatu keadaan dapat menjadi beberapa keadaan berikutnya untuk setiap simbol masukan. Oleh karena itu disebut non-deterministik . |
| Transisi string kosong tidak terlihat di DFA. | NDFA mengizinkan transisi string kosong. |
| Melacak balik diperbolehkan di DFA | Di NDFA, mundur tidak selalu memungkinkan. |
| Membutuhkan lebih banyak ruang. | Membutuhkan lebih sedikit ruang. |
| Sebuah string diterima oleh DFA, jika ditransfer ke status akhir. | Sebuah string diterima oleh NDFA, jika setidaknya satu dari semua kemungkinan transisi berakhir dalam keadaan akhir. |
Akseptor, Pengklasifikasi, dan Transduser
Penerima (Pengenal)
Sebuah robot yang menghitung fungsi Boolean disebut acceptor. Semua status akseptor menerima atau menolak masukan yang diberikan kepadanya.
Penggolong
SEBUAH classifier memiliki lebih dari dua status akhir dan memberikan satu keluaran saat berakhir.
Transduser
Sebuah otomat yang menghasilkan keluaran berdasarkan masukan saat ini dan / atau keadaan sebelumnya disebut a transducer. Transduser dapat terdiri dari dua jenis -
Mealy Machine - Output tergantung pada kondisi saat ini dan input saat ini.
Moore Machine - Outputnya hanya bergantung pada kondisi saat ini.
Dapat diterima oleh DFA dan NDFA
Sebuah string diterima oleh DFA / NDFA jika DFA / NDFA yang dimulai dari status awal berakhir dalam status menerima (salah satu status akhir) setelah seluruh string membaca.
Senar S diterima oleh DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
Bahasa L diterima oleh DFA / NDFA adalah
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
String S ′ tidak diterima oleh DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
Bahasa L 'tidak diterima oleh DFA / NDFA (Pelengkap bahasa yang diterima L) adalah
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Mari kita pertimbangkan DFA yang ditunjukkan pada Gambar 1.3. Dari DFA, string yang dapat diterima dapat diturunkan.

String yang diterima oleh DFA di atas: {0, 00, 11, 010, 101, ...........}
String tidak diterima oleh DFA di atas: {1, 011, 111, ........}
Pernyataan masalah
Membiarkan X = (Qx, ∑, δx, q0, Fx)menjadi NDFA yang menerima bahasa L (X). Kami harus merancang DFA yang setaraY = (Qy, ∑, δy, q0, Fy) seperti yang L(Y) = L(X). Prosedur berikut mengubah NDFA menjadi DFA yang setara -
Algoritma
Input - NDFA
Output - DFA setara
Step 1 - Buat tabel negara dari NDFA yang diberikan.
Step 2 - Buat tabel status kosong di bawah abjad masukan yang mungkin untuk DFA yang setara.
Step 3 - Tandai status awal DFA dengan q0 (Sama seperti NDFA).
Step 4- Cari tahu kombinasi Serikat {Q 0 , Q 1 , ..., Q n } untuk setiap alfabet masukan yang mungkin.
Step 5 - Setiap kali kami membuat status DFA baru di bawah kolom alfabet masukan, kami harus menerapkan langkah 4 lagi, jika tidak lanjutkan ke langkah 6.
Step 6 - Negara bagian yang berisi salah satu status akhir NDFA adalah status akhir dari DFA setara.
Contoh
Mari kita perhatikan NDFA yang ditunjukkan pada gambar di bawah ini.

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| Sebuah | {a, b, c, d, e} | {d, e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| e | ∅ | ∅ |
Dengan menggunakan algoritma di atas, kami menemukan DFA yang setara. Tabel status DFA ditunjukkan di bawah ini.
| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| [Sebuah] | [a, b, c, d, e] | [d, e] |
| [a, b, c, d, e] | [a, b, c, d, e] | [b, d, e] |
| [d, e] | [e] | ∅ |
| [b, d, e] | [c, e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
Diagram status DFA adalah sebagai berikut -

Minimasi DFA menggunakan Teorema Myhill-Nerode
Algoritma
Input - DFA
Output - DFA diminimalkan
Step 1- Gambarlah tabel untuk semua pasangan negara (Q i , Q j ) tidak harus terhubung langsung [Semua tidak ditandai pada awalnya]
Step 2- Pertimbangkan setiap pasangan negara bagian (Q i , Q j ) di DFA di mana Q i ∈ F dan Q j ∉ F atau sebaliknya dan tandai mereka. [Di sini F adalah himpunan keadaan akhir]
Step 3 - Ulangi langkah ini hingga kami tidak dapat menandai status lagi -
Jika ada pasangan tak bertanda (Q i , Q j ), tandai jika pasangan {δ (Q i , A), δ (Q i , A)} ditandai untuk beberapa alfabet masukan.
Step 4- Gabungkan semua pasangan tak bertanda (Q i , Q j ) dan jadikan mereka satu keadaan di DFA yang dikurangi.
Contoh
Mari kita gunakan Algoritma 2 untuk meminimalkan DFA yang ditunjukkan di bawah ini.

Step 1 - Kami menggambar tabel untuk semua pasangan negara bagian.
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
Step 2 - Kami menandai pasangan negara bagian.
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
Step 3- Kami akan mencoba menandai pasangan negara, dengan tanda centang berwarna hijau, secara transitif. Jika kita memasukkan 1 untuk menyatakan 'a' dan 'f', itu akan menjadi 'c' dan 'f' masing-masing. (c, f) sudah ditandai, maka kita akan menandai pair (a, f). Sekarang, kita masukan 1 untuk menyatakan 'b' dan 'f'; itu akan masuk ke status 'd' dan 'f' masing-masing. (d, f) sudah ditandai, maka kita akan menandai pasangan (b, f).
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
Setelah langkah 3, kita mendapatkan kombinasi status {a, b} {c, d} {c, e} {d, e} yang tidak bertanda.
Kita bisa menggabungkan kembali {c, d} {c, e} {d, e} menjadi {c, d, e}
Karenanya kita mendapat dua status gabungan sebagai - {a, b} dan {c, d, e}
Jadi DFA terakhir yang diminimalkan akan berisi tiga status {f}, {a, b} dan {c, d, e}
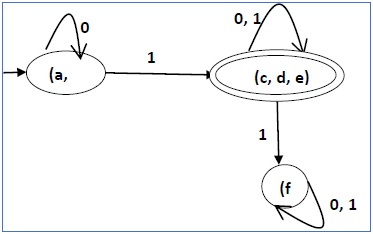
Minimasi DFA menggunakan Teorema Ekuivalensi
Jika X dan Y adalah dua kondisi dalam DFA, kita dapat menggabungkan kedua kondisi ini menjadi {X, Y} jika keduanya tidak dapat dibedakan. Dua keadaan dapat dibedakan, jika ada setidaknya satu string S, sehingga salah satu δ (X, S) dan δ (Y, S) menerima dan yang lain tidak menerima. Oleh karena itu, DFA minimal jika dan hanya jika semua negara bagian dapat dibedakan.
Algoritma 3
Step 1 - Semua negara bagian Q dibagi menjadi dua partisi - final states dan non-final states dan dilambangkan dengan P0. Semua status dalam partisi adalah ekuivalen ke- 0 . Ambil counterk dan menginisialisasi dengan 0.
Step 2- Kenaikan k dengan 1. Untuk setiap partisi di P k , bagi negara bagian di P k menjadi dua partisi jika dapat dibedakan k. Dua status dalam partisi ini X dan Y dapat dibedakan k jika ada inputS seperti yang δ(X, S) dan δ(Y, S) adalah (k-1) -dibedakan.
Step 3- Jika P k ≠ P k-1 , ulangi Langkah 2, jika tidak lanjutkan ke Langkah 4.
Step 4- Campurkan k th set setara dan membuat mereka negara-negara baru berkurang DFA.
Contoh
Mari kita pertimbangkan DFA berikut -

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| Sebuah | b | c |
| b | Sebuah | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
Mari kita terapkan algoritma di atas ke DFA di atas -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Oleh karena itu, P 1 = P 2 .
Ada tiga negara bagian dalam DFA yang dikurangi. DFA yang berkurang adalah sebagai berikut -
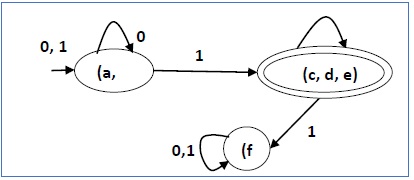
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (f) |
| (f) | (f) | (f) |
Automata hingga mungkin memiliki keluaran yang sesuai dengan setiap transisi. Ada dua jenis mesin keadaan hingga yang menghasilkan keluaran -
- Mesin Mealy
- Mesin Moore
Mesin Mealy
Mesin Mealy adalah FSM yang keluarannya bergantung pada kondisi saat ini serta masukan saat ini.
Ini dapat dijelaskan dengan 6 tupel (Q, ∑, O, δ, X, q 0 ) di mana -
Q adalah sekumpulan negara yang terbatas.
∑ adalah seperangkat simbol terbatas yang disebut alfabet masukan.
O adalah seperangkat simbol terbatas yang disebut alfabet keluaran.
δ adalah fungsi transisi masukan di mana δ: Q × ∑ → Q
X adalah fungsi transisi keluaran di mana X: Q × ∑ → O
q0adalah keadaan awal dari mana input diproses (q 0 ∈ Q).
Tabel status Mesin Mealy ditunjukkan di bawah ini -
| Keadaan sekarang | Negara bagian selanjutnya | |||
|---|---|---|---|---|
| masukan = 0 | masukan = 1 | |||
| Negara | Keluaran | Negara | Keluaran | |
| → a | b | x 1 | c | x 1 |
| b | b | x 2 | d | x 3 |
| c | d | x 3 | c | x 1 |
| d | d | x 3 | d | x 2 |
Diagram status Mesin Mealy di atas adalah -

Mesin Moore
Mesin Moore adalah FSM yang keluarannya hanya bergantung pada kondisi saat ini.
Mesin Moore dapat digambarkan dengan 6 tupel (Q, ∑, O, δ, X, q 0 ) di mana -
Q adalah sekumpulan negara yang terbatas.
∑ adalah seperangkat simbol terbatas yang disebut alfabet masukan.
O adalah seperangkat simbol terbatas yang disebut alfabet keluaran.
δ adalah fungsi transisi masukan di mana δ: Q × ∑ → Q
X adalah fungsi transisi keluaran di mana X: Q → O
q0adalah keadaan awal dari mana input diproses (q 0 ∈ Q).
Tabel status Mesin Moore ditunjukkan di bawah ini -
| Keadaan sekarang | Status Berikutnya | Keluaran | |
|---|---|---|---|
| Masukan = 0 | Masukan = 1 | ||
| → a | b | c | x 2 |
| b | b | d | x 1 |
| c | c | d | x 2 |
| d | d | d | x 3 |
Diagram status dari Mesin Moore di atas adalah -

Mesin Mealy vs Mesin Moore
Tabel berikut menyoroti poin-poin yang membedakan Mesin Mealy dari Mesin Moore.
| Mesin Mealy | Mesin Moore |
|---|---|
| Keluaran bergantung pada keadaan saat ini dan masukan saat ini | Keluaran hanya bergantung pada keadaan saat ini. |
| Umumnya, ia memiliki status yang lebih sedikit daripada Moore Machine. | Secara umum, ia memiliki lebih banyak status daripada Mesin Mealy. |
| Nilai fungsi keluaran merupakan fungsi transisi dan perubahan, ketika logika masukan pada keadaan sekarang dilakukan. | Nilai fungsi keluaran adalah fungsi dari keadaan saat ini dan perubahan di tepi jam, setiap kali perubahan keadaan terjadi. |
| Mesin mealy bereaksi lebih cepat terhadap input. Mereka umumnya bereaksi dalam siklus jam yang sama. | Di mesin Moore, lebih banyak logika diperlukan untuk memecahkan kode output yang menghasilkan lebih banyak penundaan sirkuit. Mereka umumnya bereaksi satu siklus jam kemudian. |
Mesin Moore ke Mesin Mealy
Algoritma 4
Input - Mesin Moore
Output - Mesin Mealy
Step 1 - Ambil format tabel transisi Mealy Machine kosong.
Step 2 - Salin semua status transisi Mesin Moore ke dalam format tabel ini.
Step 3- Periksa status saat ini dan keluarannya yang sesuai di tabel status Mesin Moore; jika untuk output Q i status adalah m, salin ke kolom output dari tabel status Mealy Machine di mana pun Q i muncul di status berikutnya.
Contoh
Mari kita pertimbangkan mesin Moore berikut -
| Keadaan Sekarang | Status Berikutnya | Keluaran | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b | 1 |
| b | Sebuah | d | 0 |
| c | c | c | 0 |
| d | b | Sebuah | 1 |
Sekarang kami menerapkan Algoritma 4 untuk mengubahnya menjadi Mesin Mealy.
Step 1 & 2 -
| Keadaan Sekarang | Status Berikutnya | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Negara | Keluaran | Negara | Keluaran | |
| → a | d | b | ||
| b | Sebuah | d | ||
| c | c | c | ||
| d | b | Sebuah | ||
Step 3 -
| Keadaan Sekarang | Status Berikutnya | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Negara | Keluaran | Negara | Keluaran | |
| => a | d | 1 | b | 0 |
| b | Sebuah | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | b | 0 | Sebuah | 1 |
Mesin Mealy ke Mesin Moore
Algoritma 5
Input - Mesin Mealy
Output - Mesin Moore
Step 1- Hitung jumlah output berbeda untuk setiap status (Q i ) yang tersedia di tabel status mesin Mealy.
Step 2- Jika semua keluaran Qi sama, salin status Q i . Jika ia memiliki n keluaran yang berbeda, bagi Q i menjadi n status sebagai Q di manan = 0, 1, 2 .......
Step 3 - Jika keluaran dari keadaan awal adalah 1, masukkan keadaan awal baru di awal yang memberikan 0 keluaran.
Contoh
Mari kita simak Mesin Mealy berikut -
| Keadaan Sekarang | Status Berikutnya | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Status Berikutnya | Keluaran | Status Berikutnya | Keluaran | |
| → a | d | 0 | b | 1 |
| b | Sebuah | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | b | 0 | Sebuah | 1 |
Di sini, status 'a' dan 'd' hanya memberikan 1 dan 0 output, jadi kita mempertahankan status 'a' dan 'd'. Tetapi status 'b' dan 'c' menghasilkan keluaran yang berbeda (1 dan 0). Jadi, kami membagib ke b0, b1 dan c ke c0, c1.
| Keadaan Sekarang | Status Berikutnya | Keluaran | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b 1 | 1 |
| b 0 | Sebuah | d | 0 |
| b 1 | Sebuah | d | 1 |
| c 0 | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| d | b 0 | Sebuah | 0 |
Dalam pengertian sastra dari istilah tersebut, tata bahasa menunjukkan aturan sintaksis untuk percakapan dalam bahasa alami. Linguistik telah berusaha untuk mendefinisikan tata bahasa sejak dimulainya bahasa alami seperti Inggris, Sanskerta, Mandarin, dll.
Teori bahasa formal dapat diterapkan secara luas dalam bidang Ilmu Komputer. Noam Chomsky memberikan model matematika tata bahasa tahun 1956 yang efektif untuk menulis bahasa komputer.
Tatabahasa
Tata bahasa G dapat secara formal ditulis sebagai 4-tuple (N, T, S, P) di mana -
N atau VN adalah satu set variabel atau simbol non-terminal.
T atau ∑ adalah satu set simbol Terminal.
S adalah variabel khusus yang disebut simbol Start, S ∈ N
Padalah aturan Produksi untuk Terminal dan Non-terminal. Sebuah aturan produksi memiliki bentuk α → β, di mana α dan β adalah string pada V N ∪ Σ dan setidaknya satu simbol α milik V N .
Contoh
Tata Bahasa G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Sini,
S, A, dan B adalah simbol Non-terminal;
a dan b adalah simbol Terminal
S adalah simbol Start, S ∈ N
Produksi, P : S → AB, A → a, B → b
Contoh
Tata Bahasa G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Sini,
S dan A adalah simbol Non-terminal.
a dan b adalah simbol Terminal.
ε adalah string kosong.
S adalah simbol Start, S ∈ N
Produksi P : S → aAb, aA → aaAb, A → ε
Turunan dari Tata Bahasa
String dapat diturunkan dari string lain menggunakan produksi dalam tata bahasa. Jika tata bahasaG berproduksi α → β, kita bisa bilang begitu x α y berasal x β y di G. Derivasi ini ditulis sebagai -
x α y ⇒G x β y
Contoh
Mari kita pertimbangkan tata bahasanya -
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Beberapa string yang dapat diturunkan adalah -
S ⇒ aA b menggunakan produksi S → aAb
⇒ aA bb menggunakan produksi aA → aAb
⇒ aaa A bbb menggunakan produksi aA → aAb
⇒ aaabbb menggunakan produksi A → ε
The set of all strings that can be derived from a grammar is said to be the language generated from that grammar. A language generated by a grammar G is a subset formally defined by
L(G)={W|W ∈ ∑*, S ⇒G W}
If L(G1) = L(G2), the Grammar G1 is equivalent to the Grammar G2.
Example
If there is a grammar
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
Here S produces AB, and we can replace A by a, and B by b. Here, the only accepted string is ab, i.e.,
L(G) = {ab}
Example
Suppose we have the following grammar −
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA|a, B → bB|b}
The language generated by this grammar −
L(G) = {ab, a2b, ab2, a2b2, ………}
= {am bn | m ≥ 1 and n ≥ 1}
Construction of a Grammar Generating a Language
We’ll consider some languages and convert it into a grammar G which produces those languages.
Example
Problem − Suppose, L (G) = {am bn | m ≥ 0 and n > 0}. We have to find out the grammar G which produces L(G).
Solution
Since L(G) = {am bn | m ≥ 0 and n > 0}
the set of strings accepted can be rewritten as −
L(G) = {b, ab,bb, aab, abb, …….}
Here, the start symbol has to take at least one ‘b’ preceded by any number of ‘a’ including null.
To accept the string set {b, ab, bb, aab, abb, …….}, we have taken the productions −
S → aS , S → B, B → b and B → bB
S → B → b (Accepted)
S → B → bB → bb (Accepted)
S → aS → aB → ab (Accepted)
S → aS → aaS → aaB → aab(Accepted)
S → aS → aB → abB → abb (Accepted)
Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.
Hence the grammar −
G: ({S, A, B}, {a, b}, S, { S → aS | B , B → b | bB })
Example
Problem − Suppose, L (G) = {am bn | m > 0 and n ≥ 0}. We have to find out the grammar G which produces L(G).
Solution −
Since L(G) = {am bn | m > 0 and n ≥ 0}, the set of strings accepted can be rewritten as −
L(G) = {a, aa, ab, aaa, aab ,abb, …….}
Here, the start symbol has to take at least one ‘a’ followed by any number of ‘b’ including null.
To accept the string set {a, aa, ab, aaa, aab, abb, …….}, we have taken the productions −
S → aA, A → aA , A → B, B → bB ,B → λ
S → aA → aB → aλ → a (Accepted)
S → aA → aaA → aaB → aaλ → aa (Accepted)
S → aA → aB → abB → abλ → ab (Accepted)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Accepted)
S → aA → aaA → aaB → aabB → aabλ → aab (Accepted)
S → aA → aB → abB → abbB → abbλ → abb (Accepted)
Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.
Hence the grammar −
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB })
According to Noam Chomosky, there are four types of grammars − Type 0, Type 1, Type 2, and Type 3. The following table shows how they differ from each other −
| Grammar Type | Grammar Accepted | Language Accepted | Automaton |
|---|---|---|---|
| Type 0 | Unrestricted grammar | Recursively enumerable language | Turing Machine |
| Type 1 | Context-sensitive grammar | Context-sensitive language | Linear-bounded automaton |
| Type 2 | Context-free grammar | Context-free language | Pushdown automaton |
| Type 3 | Regular grammar | Regular language | Finite state automaton |
Take a look at the following illustration. It shows the scope of each type of grammar −

Type - 3 Grammar
Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.
The productions must be in the form X → a or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule S → ε is allowed if S does not appear on the right side of any rule.
Example
X → ε
X → a | aY
Y → bType - 2 Grammar
Type-2 grammars generate context-free languages.
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.
Example
S → X a
X → a
X → aX
X → abc
X → εType - 1 Grammar
Type-1 grammars generate context-sensitive languages. The productions must be in the form
α A β → α γ β
where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.
Example
AB → AbBc
A → bcA
B → bType - 0 Grammar
Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.
Example
S → ACaB
Bc → acB
CB → DB
aD → DbA Regular Expression can be recursively defined as follows −
ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Some RE Examples
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..} |
Any set that represents the value of the Regular Expression is called a Regular Set.
Properties of Regular Sets
Property 1. The union of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
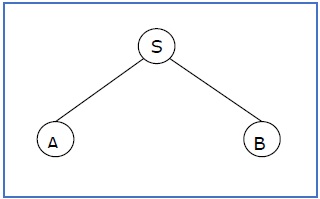
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

Derivasi paling kanan untuk string di atas "a+a*a" mungkin -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

Tata Bahasa Rekursif Kiri dan Kanan
Dalam tata bahasa tanpa konteks G, jika ada produksi dalam bentuk X → Xa dimana X adalah non-terminal dan ‘a’ adalah string terminal, ini disebut a left recursive production. Tata bahasa yang memiliki produksi rekursif kiri disebut aleft recursive grammar.
Dan jika dalam tata bahasa bebas konteks G, jika ada produksi dalam bentuk X → aX dimana X adalah non-terminal dan ‘a’ adalah string terminal, ini disebut a right recursive production. Tata bahasa yang memiliki produksi rekursif yang tepat disebut aright recursive grammar.
Jika tata bahasa bebas konteks G memiliki lebih dari satu pohon derivasi untuk beberapa string w ∈ L(G), itu disebut ambiguous grammar. Ada beberapa derivasi paling kanan atau paling kiri untuk beberapa string yang dihasilkan dari tata bahasa itu.
Masalah
Periksa apakah tata bahasa G dengan aturan produksi -
X → X + X | X * X | X | Sebuah
ambigu atau tidak.
Larutan
Mari kita cari tahu pohon turunan untuk string "a + a * a". Ini memiliki dua derivasi paling kiri.
Derivation 1- X → X + X → a + X → a + X * X → a + a * X → a + a * a
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → a + X * X → a + a * X → a + a * a
Parse tree 2 -

Karena ada dua pohon parse untuk satu string "a + a * a", tata bahasanya G ambigu.
Bahasa bebas konteks adalah closed di bawah -
- Union
- Concatenation
- Operasi Kleene Star
Persatuan
Misalkan L 1 dan L 2 menjadi dua bahasa bebas konteks. Kemudian L 1 ∪ L 2 juga bebas konteks.
Contoh
Misalkan L 1 = {a n b n , n> 0}. Tata bahasa yang sesuai G 1 akan memiliki P: S1 → aAb | ab
Misalkan L 2 = {c m d m , m ≥ 0}. Tata bahasa yang sesuai G 2 akan memiliki P: S2 → cBb | ε
Gabungan L 1 dan L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
Tata bahasa G yang sesuai akan memiliki produksi tambahan S → S1 | S2
Rangkaian
Jika L 1 dan L 2 adalah bahasa bebas konteks, maka L 1 L 2 juga bebas konteks.
Contoh
Gabungan bahasa L 1 dan L 2 , L = L 1 L 2 = {a n b n c m d m }
Tata bahasa G yang sesuai akan memiliki produksi tambahan S → S1 S2
Kleene Star
Jika L adalah bahasa tanpa konteks, maka L * juga bebas konteks.
Contoh
Misalkan L = {a n b n , n ≥ 0}. Tata bahasa yang sesuai G akan memiliki P: S → aAb | ε
Bintang Kleene L 1 = {a n b n } *
Tata bahasa yang sesuai G 1 akan memiliki produksi tambahan S1 → SS 1 | ε
Bahasa bebas konteks adalah not closed di bawah -
Intersection - Jika L1 dan L2 adalah bahasa bebas konteks, maka L1 ∩ L2 belum tentu bebas konteks.
Intersection with Regular Language - Jika L1 adalah bahasa biasa dan L2 adalah bahasa bebas konteks, maka L1 ∩ L2 adalah bahasa bebas konteks.
Complement - Jika L1 adalah bahasa bebas konteks, maka L1 'mungkin tidak bebas konteks.
Dalam CFG, mungkin saja semua aturan dan simbol produksi tidak diperlukan untuk derivasi string. Selain itu, mungkin ada beberapa produksi nol dan produksi unit. Penghapusan produksi dan simbol ini disebutsimplification of CFGs. Penyederhanaan pada dasarnya terdiri dari langkah-langkah berikut -
- Pengurangan CFG
- Penghapusan Produksi Unit
- Penghapusan Produksi Null
Pengurangan CFG
CFG dikurangi dalam dua fase -
Phase 1 - Penurunan tata bahasa yang setara, G’, dari CFG, G, sedemikian rupa sehingga setiap variabel mendapatkan beberapa string terminal.
Derivation Procedure -
Langkah 1 - Sertakan semua simbol, W1, yang memperoleh beberapa terminal dan menginisialisasi i=1.
Langkah 2 - Sertakan semua simbol, Wi+1, yang diturunkan Wi.
Langkah 3 - Kenaikan i dan ulangi Langkah 2, sampai Wi+1 = Wi.
Langkah 4 - Sertakan semua aturan produksi yang ada Wi di dalamnya.
Phase 2 - Penurunan tata bahasa yang setara, G”, dari CFG, G’, sedemikian rupa sehingga setiap simbol muncul dalam bentuk sentensial.
Derivation Procedure -
Langkah 1 - Sertakan simbol awal Y1 dan menginisialisasi i = 1.
Langkah 2 - Sertakan semua simbol, Yi+1, itu bisa diturunkan dari Yi dan menyertakan semua aturan produksi yang telah diterapkan.
Langkah 3 - Kenaikan i dan ulangi Langkah 2, sampai Yi+1 = Yi.
Masalah
Cari tata bahasa tereduksi yang setara dengan tata bahasa G, yang memiliki aturan produksi, P: S → AC | B, A → a, C → c | BC, E → aA | e
Larutan
Phase 1 -
T = {a, c, e}
W 1 = {A, C, E} dari aturan A → a, C → c dan E → aA
W 2 = {A, C, E} U {S} dari aturan S → AC
W 3 = {A, C, E, S} U ∅
Karena W 2 = W 3 , kita dapat menurunkan G 'sebagai -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
dimana P: S → AC, A → a, C → c, E → aA | e
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} dari aturan S → AC
Y 3 = {S, A, C, a, c} dari aturan A → a dan C → c
Y 4 = {S, A, C, a, c}
Karena Y 3 = Y 4 , kita dapat menurunkan G "sebagai -
G ”= {{A, C, S}, {a, c}, P, {S}}
dimana P: S → AC, A → a, C → c
Penghapusan Produksi Unit
Setiap aturan produksi dalam bentuk A → B di mana A, B ∈ Non-terminal dipanggil unit production..
Prosedur Penghapusan -
Step 1 - Untuk menghapus A → B, tambahkan produksi A → x ke aturan tata bahasa kapan pun B → xterjadi dalam tata bahasa. [x ∈ Terminal, x bisa Null]
Step 2 - Hapus A → B dari tata bahasa.
Step 3 - Ulangi dari langkah 1 sampai semua produksi unit dihapus.
Problem
Hapus produksi unit dari berikut ini -
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution -
Ada 3 unit produksi dalam tata bahasa -
Y → Z, Z → M, dan M → N
At first, we will remove M → N.
Sebagai N → a, kita menambahkan M → a, dan M → N dihilangkan.
Set produksi menjadi
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
Now we will remove Z → M.
Karena M → a, kita menambahkan Z → a, dan Z → M dihapus.
Set produksi menjadi
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
Now we will remove Y → Z.
Karena Z → a, kita menambahkan Y → a, dan Y → Z dihapus.
Set produksi menjadi
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
Sekarang Z, M, dan N tidak dapat dijangkau, oleh karena itu kita dapat menghapusnya.
CFG terakhir adalah produksi unit gratis -
S → XY, X → a, Y → a | b
Penghapusan Produksi Null
Dalam CFG, simbol non-terminal ‘A’ adalah variabel nullable jika ada produksi A → ε atau ada penurunan yang dimulai pada A dan akhirnya berakhir dengan
ε: A → .......… → ε
Prosedur Penghapusan
Step 1 - Cari tahu variabel non-terminal nullable yang memperoleh ε.
Step 2 - Untuk setiap produksi A → a, buat semua produksi A → x dimana x diperoleh dari ‘a’ dengan menghapus satu atau beberapa non-terminal dari Langkah 1.
Step 3 - Gabungkan produksi asli dengan hasil langkah 2 dan hapus ε - productions.
Problem
Hapus produksi nol dari berikut ini -
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Ada dua variabel nullable - A dan B
At first, we will remove B → ε.
Setelah melepas B → ε, set produksi menjadi -
S → ASA | aB | b | a, A ε B | b | & epsilon, B → b
Now we will remove A → ε.
Setelah melepas A → ε, set produksi menjadi -
S → ASA | aB | b | a | SA | SEBAGAI | S, A → B | b, B → b
Ini adalah set produksi akhir tanpa transisi nol.
CFG dalam Bentuk Normal Chomsky jika Produksi dalam bentuk berikut -
- A → a
- A → BC
- S → ε
di mana A, B, dan C adalah non-terminal dan a adalah terminal.
Algoritma untuk Mengubah ke Bentuk Normal Chomsky -
Step 1 - Jika simbol start S terjadi di beberapa sisi kanan, buat simbol awal baru S’ dan produksi baru S’→ S.
Step 2- Hapus produksi Null. (Menggunakan algoritma penghapusan produksi Null yang dibahas sebelumnya)
Step 3- Hapus produksi unit. (Menggunakan algoritma penghilangan produksi Unit yang dibahas sebelumnya)
Step 4 - Ganti setiap produksi A → B1…Bn dimana n > 2 dengan A → B1C dimana C → B2 …Bn. Ulangi langkah ini untuk semua produksi yang memiliki dua atau lebih simbol di sisi kanan.
Step 5 - Jika sisi kanan produksi ada dalam bentuk A → aB dimana a adalah terminal dan A, B bersifat non-terminal, maka produksi digantikan oleh A → XB dan X → a. Ulangi langkah ini untuk setiap produksi yang ada dalam bentukA → aB.
Masalah
Ubah CFG berikut menjadi CNF
S → ASA | aB, A → B | S, B → b | ε
Larutan
(1) Sejak S muncul di kanan, kami menambahkan status baru S0 dan S0→S ditambahkan ke set produksi dan menjadi -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Sekarang kita akan menghapus produksi nol -
B → ∈ dan A → ∈
Setelah membuang B → ε, set produksi menjadi -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
Setelah membuang A → ∈, set produksi menjadi -
S 0 → S, S → ASA | aB | a | SEBAGAI | SA | S, A → B | S, B → b
(3) Sekarang kami akan menghapus produksi unit.
Setelah melepas S → S, set produksi menjadi -
S 0 → S, S → ASA | aB | a | SEBAGAI | SA, A → B | S, B → b
Setelah melepas S 0 → S, set produksi menjadi -
S 0 → ASA | aB | a | SEBAGAI | SA, S → ASA | aB | a | SEBAGAI | SA
A → B | S, B → b
Setelah membuang A → B, set produksi menjadi -
S 0 → ASA | aB | a | SEBAGAI | SA, S → ASA | aB | a | SEBAGAI | SA
A → S | b
B → b
Setelah melepas A → S, set produksi menjadi -
S 0 → ASA | aB | a | SEBAGAI | SA, S → ASA | aB | a | SEBAGAI | SA
A → b | ASA | aB | a | SEBAGAI | SA, B → b
(4) Sekarang kita akan menemukan lebih dari dua variabel di RHS
Di sini, S 0 → ASA, S → ASA, A → ASA melanggar dua Non-terminal di RHS
Karenanya kami akan menerapkan langkah 4 dan langkah 5 untuk mendapatkan set produksi akhir berikut yang ada di CNF -
S 0 → AX | aB | a | SEBAGAI | SA
S → AX | aB | a | SEBAGAI | SA
A → b | AX | aB | a | SEBAGAI | SA
B → b
X → SA
(5)Kita harus mengubah produksi S 0 → aB, S → aB, A → aB
Dan set produksi akhir menjadi -
S 0 → AX | YB | a | SEBAGAI | SA
S → AX | YB | a | SEBAGAI | SA
A → b A → b | AX | YB | a | SEBAGAI | SA
B → b
X → SA
Y → a
CFG dalam Bentuk Normal Greibach jika Produksi dalam bentuk berikut -
A → b
A → bD 1 … D n
S → ε
dimana A, D 1 , ...., D n adalah non-terminal dan b adalah terminal.
Algoritma untuk Mengubah CFG menjadi Bentuk Normal Greibach
Step 1 - Jika simbol start S terjadi di beberapa sisi kanan, buat simbol awal baru S’ dan produksi baru S’ → S.
Step 2- Hapus produksi Null. (Menggunakan algoritma penghapusan produksi Null yang dibahas sebelumnya)
Step 3- Hapus produksi unit. (Menggunakan algoritma penghilangan produksi Unit yang dibahas sebelumnya)
Step 4 - Hapus semua rekursi kiri langsung dan tidak langsung.
Step 5 - Lakukan substitusi produksi yang tepat untuk mengubahnya menjadi bentuk GNF yang tepat.
Masalah
Ubah CFG berikut menjadi CNF
S → XY | Xn | p
X → mX | m
Y → Xn | Hai
Larutan
Sini, Stidak muncul di sisi kanan produksi apa pun dan tidak ada unit atau produksi nol dalam kumpulan aturan produksi. Jadi, kita dapat melewati Langkah 1 ke Langkah 3.
Step 4
Sekarang setelah mengganti
X dalam S → XY | Xo | p
dengan
mX | m
kami dapatkan
S → mXY | saya | mXo | mo | p.
Dan setelah mengganti
X dalam Y → X n | Hai
dengan sisi kanan
X → mX | m
kami dapatkan
Y → mXn | mn | Hai.
Dua produksi baru O → o dan P → p ditambahkan ke set produksi dan kemudian kita sampai pada GNF akhir sebagai berikut -
S → mXY | saya | mXC | mC | p
X → mX | m
Y → mXD | mD | Hai
O → o
P → hal
Kata pengantar singkat
Jika L adalah bahasa tanpa konteks, ada durasi yang memompa p sedemikian rupa sehingga string apa pun w ∈ L panjangnya ≥ p dapat ditulis sebagai w = uvxyz, dimana vy ≠ ε, |vxy| ≤ p, dan untuk semua i ≥ 0, uvixyiz ∈ L.
Aplikasi Pumping Lemma
Pumping lemma digunakan untuk memeriksa apakah sebuah tata bahasa bebas konteks atau tidak. Mari kita ambil contoh dan tunjukkan bagaimana itu dicentang.
Masalah
Cari tahu apakah bahasanya L = {xnynzn | n ≥ 1} bebas konteks atau tidak.
Larutan
Membiarkan Lbebas konteks. Kemudian,L harus memenuhi lemma pemompaan.
Pertama-tama, pilih nomor ndari lemma pemompaan. Kemudian, ambil z sebagai 0 n 1 n 2 n .
Istirahat z ke uvwxy, dimana
|vwx| ≤ n and vx ≠ ε.
Karenanya vwxtidak dapat melibatkan 0 dan 2, karena 0 terakhir dan 2 pertama setidaknya terpisah (n + 1) posisi. Ada dua kasus -
Case 1 - vwxtidak memiliki 2s. Kemudianvxhanya memiliki 0 dan 1. Kemudianuwy, yang harus masuk L, memiliki n 2 d, tapi kurang dari n 0 atau 1.
Case 2 - vwx tidak memiliki 0.
Di sini kontradiksi terjadi.
Karenanya, L bukanlah bahasa tanpa konteks.
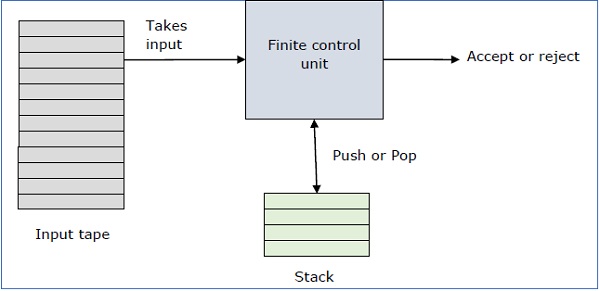
Struktur Dasar PDA
Sebuah robot pushdown adalah cara untuk mengimplementasikan tata bahasa bebas konteks dengan cara yang sama seperti kami merancang DFA untuk tata bahasa biasa. DFA dapat mengingat sejumlah informasi yang terbatas, tetapi PDA dapat mengingat jumlah informasi yang tak terbatas.
Pada dasarnya robot pushdown adalah -
"Finite state machine" + "a stack"
Sebuah robot pushdown memiliki tiga komponen -
- pita masukan,
- unit kontrol, dan
- tumpukan dengan ukuran tak terbatas.
Kepala tumpukan memindai simbol atas tumpukan.
Tumpukan melakukan dua operasi -
Push - simbol baru ditambahkan di bagian atas.
Pop - simbol atas dibaca dan dihapus.
PDA mungkin atau mungkin tidak membaca simbol input, tetapi harus membaca bagian atas tumpukan di setiap transisi.
Sebuah PDA secara formal dapat dideskripsikan sebagai 7-tupel (Q, ∑, S, δ, q 0 , I, F) -
Q adalah jumlah negara bagian yang terbatas
∑ adalah alfabet masukan
S adalah simbol tumpukan
δ adalah fungsi transisi: Q × (∑ ∪ {ε}) × S × Q × S *
q0adalah keadaan awal (q 0 ∈ Q)
I adalah simbol tumpukan atas awal (I ∈ S)
F adalah sekumpulan status menerima (F ∈ Q)
Diagram berikut menunjukkan transisi dalam PDA dari status q 1 ke status q 2 , diberi label sebagai a, b → c -

Artinya di negara bagian q1, jika kita menemukan string input ‘a’ dan simbol tumpukan atas adalah ‘b’, lalu kita meletus ‘b’, Dorong ‘c’ di atas tumpukan dan pindah ke status q2.
Terminologi Terkait PDA
Deskripsi Seketika
Deskripsi sesaat (ID) dari PDA diwakili oleh triplet (q, w, s) dimana
q adalah negara bagian
w adalah masukan yang tidak digunakan
s adalah isi tumpukan
Notasi Pintu Putar
Notasi "pintu putar" digunakan untuk menghubungkan pasangan ID yang mewakili satu atau banyak gerakan PDA. Proses transisi dilambangkan dengan simbol pintu putar "⊢".
Pertimbangkan sebuah PDA (Q, ∑, S, δ, q 0 , I, F). Transisi dapat secara matematis diwakili oleh notasi pintu putar berikut -
(p, aw, Tβ) ⊢ (q, w, αb)Ini menyiratkan bahwa saat mengambil transisi dari keadaan p untuk menyatakan q, simbol masukan ‘a’ dikonsumsi, dan bagian atas tumpukan ‘T’ diganti dengan string baru ‘α’.
Note - Jika kita ingin nol atau lebih gerakan PDA, kita harus menggunakan simbol (⊢ *) untuk itu.
Ada dua cara berbeda untuk menentukan penerimaan PDA.
Penerimaan Status Akhir
In final state acceptability, a PDA accepts a string when, after reading the entire string, the PDA is in a final state. From the starting state, we can make moves that end up in a final state with any stack values. The stack values are irrelevant as long as we end up in a final state.
For a PDA (Q, ∑, S, δ, q0, I, F), the language accepted by the set of final states F is −
L(PDA) = {w | (q0, w, I) ⊢* (q, ε, x), q ∈ F}
for any input stack string x.
Empty Stack Acceptability
Here a PDA accepts a string when, after reading the entire string, the PDA has emptied its stack.
For a PDA (Q, ∑, S, δ, q0, I, F), the language accepted by the empty stack is −
L(PDA) = {w | (q0, w, I) ⊢* (q, ε, ε), q ∈ Q}
Example
Construct a PDA that accepts L = {0n 1n | n ≥ 0}
Solution

This language accepts L = {ε, 01, 0011, 000111, ............................. }
Here, in this example, the number of ‘a’ and ‘b’ have to be same.
Initially we put a special symbol ‘$’ into the empty stack.
Then at state q2, if we encounter input 0 and top is Null, we push 0 into stack. This may iterate. And if we encounter input 1 and top is 0, we pop this 0.
Then at state q3, if we encounter input 1 and top is 0, we pop this 0. This may also iterate. And if we encounter input 1 and top is 0, we pop the top element.
If the special symbol ‘$’ is encountered at top of the stack, it is popped out and it finally goes to the accepting state q4.
Example
Construct a PDA that accepts L = { wwR | w = (a+b)* }
Solution

Initially we put a special symbol ‘$’ into the empty stack. At state q2, the w is being read. In state q3, each 0 or 1 is popped when it matches the input. If any other input is given, the PDA will go to a dead state. When we reach that special symbol ‘$’, we go to the accepting state q4.
If a grammar G is context-free, we can build an equivalent nondeterministic PDA which accepts the language that is produced by the context-free grammar G. A parser can be built for the grammar G.
Also, if P is a pushdown automaton, an equivalent context-free grammar G can be constructed where
L(G) = L(P)
In the next two topics, we will discuss how to convert from PDA to CFG and vice versa.
Algorithm to find PDA corresponding to a given CFG
Input − A CFG, G = (V, T, P, S)
Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)
Step 1 − Convert the productions of the CFG into GNF.
Step 2 − The PDA will have only one state {q}.
Step 3 − The start symbol of CFG will be the start symbol in the PDA.
Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.
Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A).
Problem
Construct a PDA from the following CFG.
G = ({S, X}, {a, b}, P, S)
where the productions are −
S → XS | ε , A → aXb | Ab | ab
Solution
Let the equivalent PDA,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
where δ −
δ(q, ε , S) = {(q, XS), (q, ε )}
δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}
δ(q, a, a) = {(q, ε )}
δ(q, 1, 1) = {(q, ε )}
Algorithm to find CFG corresponding to a given PDA
Input − A CFG, G = (V, T, P, S)
Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F) such that the non- terminals of the grammar G will be {Xwx | w,x ∈ Q} and the start state will be Aq0,F.
Step 1 − For every w, x, y, z ∈ Q, m ∈ S and a, b ∈ ∑, if δ (w, a, ε) contains (y, m) and (z, b, m) contains (x, ε), add the production rule Xwx → a Xyzb in grammar G.
Step 2 − For every w, x, y, z ∈ Q, add the production rule Xwx → XwyXyx in grammar G.
Step 3 − For w ∈ Q, add the production rule Xww → ε in grammar G.
Parsing is used to derive a string using the production rules of a grammar. It is used to check the acceptability of a string. Compiler is used to check whether or not a string is syntactically correct. A parser takes the inputs and builds a parse tree.
A parser can be of two types −
Top-Down Parser − Top-down parsing starts from the top with the start-symbol and derives a string using a parse tree.
Bottom-Up Parser − Bottom-up parsing starts from the bottom with the string and comes to the start symbol using a parse tree.
Design of Top-Down Parser
For top-down parsing, a PDA has the following four types of transitions −
Pop the non-terminal on the left hand side of the production at the top of the stack and push its right-hand side string.
If the top symbol of the stack matches with the input symbol being read, pop it.
Push the start symbol ‘S’ into the stack.
If the input string is fully read and the stack is empty, go to the final state ‘F’.
Example
Design a top-down parser for the expression "x+y*z" for the grammar G with the following production rules −
P: S → S+X | X, X → X*Y | Y, Y → (S) | id
Solution
If the PDA is (Q, ∑, S, δ, q0, I, F), then the top-down parsing is −
(x+y*z, I) ⊢(x +y*z, SI) ⊢ (x+y*z, S+XI) ⊢(x+y*z, X+XI)
⊢(x+y*z, Y+X I) ⊢(x+y*z, x+XI) ⊢(+y*z, +XI) ⊢ (y*z, XI)
⊢(y*z, X*YI) ⊢(y*z, y*YI) ⊢(*z,*YI) ⊢(z, YI) ⊢(z, zI) ⊢(ε, I)
Design of a Bottom-Up Parser
For bottom-up parsing, a PDA has the following four types of transitions −
Push the current input symbol into the stack.
Replace the right-hand side of a production at the top of the stack with its left-hand side.
If the top of the stack element matches with the current input symbol, pop it.
If the input string is fully read and only if the start symbol ‘S’ remains in the stack, pop it and go to the final state ‘F’.
Example
Design a top-down parser for the expression "x+y*z" for the grammar G with the following production rules −
P: S → S+X | X, X → X*Y | Y, Y → (S) | id
Solution
If the PDA is (Q, ∑, S, δ, q0, I, F), then the bottom-up parsing is −
(x+y*z, I) ⊢ (+y*z, xI) ⊢ (+y*z, YI) ⊢ (+y*z, XI) ⊢ (+y*z, SI)
⊢(y*z, +SI) ⊢ (*z, y+SI) ⊢ (*z, Y+SI) ⊢ (*z, X+SI) ⊢ (z, *X+SI)
⊢ (ε, z*X+SI) ⊢ (ε, Y*X+SI) ⊢ (ε, X+SI) ⊢ (ε, SI)
A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type 0 grammars. It was invented in 1936 by Alan Turing.
Definition
A Turing Machine (TM) is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine. After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.
A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q0, B, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
q0 is the initial state
B is the blank symbol
F is the set of final states
Comparison with the previous automaton
The following table shows a comparison of how a Turing machine differs from Finite Automaton and Pushdown Automaton.
| Machine | Stack Data Structure | Deterministic? |
|---|---|---|
| Finite Automaton | N.A | Yes |
| Pushdown Automaton | Last In First Out(LIFO) | No |
| Turing Machine | Infinite tape | Yes |
Example of Turing machine
Turing machine M = (Q, X, ∑, δ, q0, B, F) with
- Q = {q0, q1, q2, qf}
- X = {a, b}
- ∑ = {1}
- q0 = {q0}
- B = blank symbol
- F = {qf }
δ is given by −
| Tape alphabet symbol | Present State ‘q0’ | Present State ‘q1’ | Present State ‘q2’ |
|---|---|---|---|
| a | 1Rq1 | 1Lq0 | 1Lqf |
| b | 1Lq2 | 1Rq1 | 1Rqf |
Here the transition 1Rq1 implies that the write symbol is 1, the tape moves right, and the next state is q1. Similarly, the transition 1Lq2 implies that the write symbol is 1, the tape moves left, and the next state is q2.
Time and Space Complexity of a Turing Machine
For a Turing machine, the time complexity refers to the measure of the number of times the tape moves when the machine is initialized for some input symbols and the space complexity is the number of cells of the tape written.
Time complexity all reasonable functions −
T(n) = O(n log n)
TM's space complexity −
S(n) = O(n)
A TM accepts a language if it enters into a final state for any input string w. A language is recursively enumerable (generated by Type-0 grammar) if it is accepted by a Turing machine.
A TM decides a language if it accepts it and enters into a rejecting state for any input not in the language. A language is recursive if it is decided by a Turing machine.
There may be some cases where a TM does not stop. Such TM accepts the language, but it does not decide it.
Designing a Turing Machine
The basic guidelines of designing a Turing machine have been explained below with the help of a couple of examples.
Example 1
Design a TM to recognize all strings consisting of an odd number of α’s.
Solution
The Turing machine M can be constructed by the following moves −
Let q1 be the initial state.
If M is in q1; on scanning α, it enters the state q2 and writes B (blank).
If M is in q2; on scanning α, it enters the state q1 and writes B (blank).
From the above moves, we can see that M enters the state q1 if it scans an even number of α’s, and it enters the state q2 if it scans an odd number of α’s. Hence q2 is the only accepting state.
Hence,
M = {{q1, q2}, {1}, {1, B}, δ, q1, B, {q2}}
where δ is given by −
| Tape alphabet symbol | Present State ‘q1’ | Present State ‘q2’ |
|---|---|---|
| α | BRq2 | BRq1 |
Example 2
Design a Turing Machine that reads a string representing a binary number and erases all leading 0’s in the string. However, if the string comprises of only 0’s, it keeps one 0.
Solution
Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.
The Turing Machine, M, can be constructed by the following moves −
Let q0 be the initial state.
If M is in q0, on reading 0, it moves right, enters the state q1 and erases 0. On reading 1, it enters the state q2 and moves right.
If M is in q1, on reading 0, it moves right and erases 0, i.e., it replaces 0’s by B’s. On reaching the leftmost 1, it enters q2 and moves right. If it reaches B, i.e., the string comprises of only 0’s, it moves left and enters the state q3.
If M is in q2, on reading either 0 or 1, it moves right. On reaching B, it moves left and enters the state q4. This validates that the string comprises only of 0’s and 1’s.
If M is in q3, it replaces B by 0, moves left and reaches the final state qf.
If M is in q4, on reading either 0 or 1, it moves left. On reaching the beginning of the string, i.e., when it reads B, it reaches the final state qf.
Hence,
M = {{q0, q1, q2, q3, q4, qf}, {0,1, B}, {1, B}, δ, q0, B, {qf}}
where δ is given by −
| Tape alphabet symbol | Present State ‘q0’ | Present State ‘q1’ | Present State ‘q2’ | Present State ‘q3’ | Present State ‘q4’ |
|---|---|---|---|---|---|
| 0 | BRq1 | BRq1 | ORq2 | - | OLq4 |
| 1 | 1Rq2 | 1Rq2 | 1Rq2 | - | 1Lq4 |
| B | BRq1 | BLq3 | BLq4 | OLqf | BRqf |
Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate head. Each head can move independently of the other heads. Initially the input is on tape 1 and others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank. Next, the machine reads consecutive symbols under its heads and the TM prints a symbol on each tape and moves its heads.

A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
B is the blank symbol
δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k
where there is k number of tapes
q0 is the initial state
F is the set of final states
Note − Every Multi-tape Turing machine has an equivalent single-tape Turing machine.
Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a relation on states and symbols where
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], Left_shift or Right_shift)
q0 is the initial state
F is the set of final states
Note − For every single-track Turing Machine S, there is an equivalent multi-track Turing Machine M such that L(S) = L(M).
In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.
A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function;
δ : Q × X → P(Q × X × {Left_shift, Right_shift}).
q0 is the initial state
B is the blank symbol
F is the set of final states
A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.

It is a two-track tape −
Upper track − It represents the cells to the right of the initial head position.
Lower track − It represents the cells to the left of the initial head position in reverse order.
The infinite length input string is initially written on the tape in contiguous tape cells.
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machines.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some bounded finite length.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The computation is restricted to the constant bounded area. The input alphabet contains two special symbols which serve as left end markers and right end markers which mean the transitions neither move to the left of the left end marker nor to the right of the right end marker of the tape.
A linear bounded automaton can be defined as an 8-tuple (Q, X, ∑, q0, ML, MR, δ, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
q0 is the initial state
ML is the left end marker
MR is the right end marker where MR ≠ ML
δ is a transition function which maps each pair (state, tape symbol) to (state, tape symbol, Constant ‘c’) where c can be 0 or +1 or -1
F is the set of final states

A deterministic linear bounded automaton is always context-sensitive and the linear bounded automaton with empty language is undecidable..
A language is called Decidable or Recursive if there is a Turing machine which accepts and halts on every input string w. Every decidable language is Turing-Acceptable.

A decision problem P is decidable if the language L of all yes instances to P is decidable.
For a decidable language, for each input string, the TM halts either at the accept or the reject state as depicted in the following diagram −

Example 1
Find out whether the following problem is decidable or not −
Is a number ‘m’ prime?
Solution
Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
Divide the number ‘m’ by all the numbers between ‘2’ and ‘√m’ starting from ‘2’.
If any of these numbers produce a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the answer could be made by ‘Yes’ or ‘No’.
Hence, it is a decidable problem.
Example 2
Given a regular language L and string w, how can we check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted

Some more decidable problems are −
- Does DFA accept the empty language?
- Is L1 ∩ L2 = ∅ for regular sets?
Note −
If a language L is decidable, then its complement L' is also decidable
If a language is decidable, then there is an enumerator for it.
For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example
- The halting problem of Turing machine
- The mortality problem
- The mortal matrix problem
- The Post correspondence problem, etc.
Input − A Turing machine and an input string w.
Problem − Does the Turing machine finish computing of the string w in a finite number of steps? The answer must be either yes or no.
Proof − At first, we will assume that such a Turing machine exists to solve this problem and then we will show it is contradicting itself. We will call this Turing machine as a Halting machine that produces a ‘yes’ or ‘no’ in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as ‘yes’, otherwise as ‘no’. The following is the block diagram of a Halting machine −

Now we will design an inverted halting machine (HM)’ as −
If H returns YES, then loop forever.
If H returns NO, then halt.
The following is the block diagram of an ‘Inverted halting machine’ −

Further, a machine (HM)2 which input itself is constructed as follows −
- If (HM)2 halts on input, loop forever.
- Else, halt.
Here, we have got a contradiction. Hence, the halting problem is undecidable.
Rice theorem states that any non-trivial semantic property of a language which is recognized by a Turing machine is undecidable. A property, P, is the language of all Turing machines that satisfy that property.
Formal Definition
If P is a non-trivial property, and the language holding the property, Lp , is recognized by Turing machine M, then Lp = {<M> | L(M) ∈ P} is undecidable.
Description and Properties
Property of languages, P, is simply a set of languages. If any language belongs to P (L ∈ P), it is said that L satisfies the property P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold:
Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L )
Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.
Let, w be an input in a particular instant and N is a Turing Machine which follows −
On input x
- Run M on w
- If M does not accept (or doesn't halt), then do not accept x (or do not halt)
- If M accepts w then run M0 on x. If M0 accepts x, then accept x.
A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that
- If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
- If M does not accept w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.
The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Here,
x2x1x3 = ‘aaabbaaa’
and y2y1y3 = ‘aaabbaaa’
We can see that
x2x1x3 = y2y1y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 2
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
In this case, there is no solution because −
| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.