Pengenalan Tata Bahasa Bebas Konteks
Definition - Tata bahasa bebas konteks (CFG) yang terdiri dari seperangkat aturan tata bahasa yang terbatas adalah empat kali lipat (N, T, P, S) dimana
N adalah satu set simbol non-terminal.
T adalah satu set terminal dimana N ∩ T = NULL.
P adalah seperangkat aturan, P: N → (N ∪ T)*, yaitu, sisi kiri aturan produksi P memang memiliki konteks kanan atau konteks kiri.
S adalah simbol awal.
Example
- Tata bahasa ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
- Tata bahasa ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- Tata bahasa ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generasi Pohon Turunan
Pohon derivasi atau pohon parse adalah pohon berakar berurutan yang secara grafis mewakili informasi semantik string yang diturunkan dari tata bahasa bebas konteks.
Teknik Representasi
Root vertex - Harus diberi label dengan simbol awal.
Vertex - Dilabeli dengan simbol non-terminal.
Leaves - Diberi label dengan simbol terminal atau ε.
Jika S → x 1 x 2 …… x n merupakan aturan produksi dalam sebuah CFG, maka pohon parse / pohon turunannya adalah sebagai berikut -

Ada dua pendekatan berbeda untuk menggambar pohon derivasi -
Top-down Approach −
Dimulai dengan simbol awal S
Turun ke daun pohon menggunakan produksi
Bottom-up Approach −
Mulai dari daun pohon
Lanjutkan ke atas ke akar yang merupakan simbol awal S
Penurunan atau Hasil dari Pohon
Derivasi atau hasil pohon parse adalah string terakhir yang diperoleh dengan menggabungkan label daun pohon dari kiri ke kanan, mengabaikan Nulls. Namun, jika semua daunnya Null, turunannya Null.
Example
Misalkan CFG {N, T, P, S}
N = {S}, T = {a, b}, Simbol awal = S, P = S → SS | aSb | ε
Salah satu turunan dari CFG di atas adalah "abaabb"
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Bentuk Sentensial dan Pohon Derivasi Parsial
Pohon turunan parsial adalah sub-pohon dari pohon derivasi / pohon parse sedemikian rupa sehingga semua anaknya berada di dalam sub-pohon atau tidak satupun dari mereka berada di sub-pohon.
Example
Jika dalam CFG mana pun produksinya -
S → AB, A → aaA | ε, B → Bb | ε
pohon derivasi parsial bisa menjadi berikut -
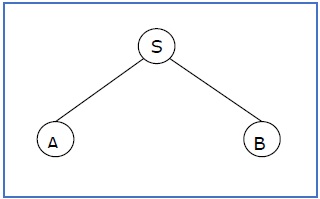
Jika pohon turunan parsial mengandung akar S, itu disebut a sentential form. Sub-pohon di atas juga dalam bentuk sentensial.
Turunan String Paling Kiri dan Kanan
Leftmost derivation - Derivasi paling kiri diperoleh dengan menerapkan produksi ke variabel paling kiri di setiap langkah.
Rightmost derivation - Derivasi paling kanan diperoleh dengan menerapkan produksi ke variabel paling kanan di setiap langkah.
Example
Biarkan semua aturan produksi dalam CFG dibuat
X → X + X | X * X | X | Sebuah
di atas alfabet {a}.
Derivasi paling kiri untuk string "a+a*a" mungkin -
X → X + X → a + X → a + X * X → a + a * X → a + a * a
Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

Derivasi paling kanan untuk string di atas "a+a*a" mungkin -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

Tata Bahasa Rekursif Kiri dan Kanan
Dalam tata bahasa tanpa konteks G, jika ada produksi dalam bentuk X → Xa dimana X adalah non-terminal dan ‘a’ adalah string terminal, ini disebut a left recursive production. Tata bahasa yang memiliki produksi rekursif kiri disebut aleft recursive grammar.
Dan jika dalam tata bahasa bebas konteks G, jika ada produksi dalam bentuk X → aX dimana X adalah non-terminal dan ‘a’ adalah string terminal, ini disebut a right recursive production. Tata bahasa yang memiliki produksi rekursif yang tepat disebut aright recursive grammar.