Minimasi DFA
Minimasi DFA menggunakan Teorema Myphill-Nerode
Algoritma
Input - DFA
Output - DFA diminimalkan
Step 1- Gambarlah tabel untuk semua pasangan negara (Q i , Q j ) tidak harus terhubung langsung [Semua tidak ditandai pada awalnya]
Step 2- Pertimbangkan setiap pasangan negara bagian (Q i , Q j ) di DFA di mana Q i ∈ F dan Q j ∉ F atau sebaliknya dan tandai mereka. [Di sini F adalah himpunan keadaan akhir]
Step 3 - Ulangi langkah ini sampai kami tidak dapat menandai status lagi -
Jika ada pasangan tak bertanda (Q i , Q j ), tandai jika pasangan {δ (Q i , A), δ (Q i , A)} ditandai untuk beberapa alfabet masukan.
Step 4- Gabungkan semua pasangan tak bertanda (Q i , Q j ) dan jadikan mereka satu keadaan di DFA yang dikurangi.
Contoh
Mari kita gunakan Algoritma 2 untuk meminimalkan DFA yang ditunjukkan di bawah ini.

Step 1 - Kami menggambar tabel untuk semua pasangan negara bagian.
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
Step 2 - Kami menandai pasangan negara bagian.
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
Step 3- Kami akan mencoba menandai pasangan negara bagian, dengan tanda centang berwarna hijau, secara transitif. Jika kita memasukkan 1 untuk menyatakan 'a' dan 'f', itu akan menjadi 'c' dan 'f' masing-masing. (c, f) sudah ditandai, maka kita akan menandai pair (a, f). Sekarang, kita masukan 1 untuk menyatakan 'b' dan 'f'; itu akan menjadi 'd' dan 'f' masing-masing. (d, f) sudah ditandai, maka kita akan menandai pasangan (b, f).
| Sebuah | b | c | d | e | f | |
| Sebuah | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
Setelah langkah 3, kita mendapatkan kombinasi status {a, b} {c, d} {c, e} {d, e} yang tidak bertanda.
Kita bisa menggabungkan kembali {c, d} {c, e} {d, e} menjadi {c, d, e}
Karenanya kita mendapat dua status gabungan sebagai - {a, b} dan {c, d, e}
Jadi DFA terakhir yang diminimalkan akan berisi tiga status {f}, {a, b} dan {c, d, e}
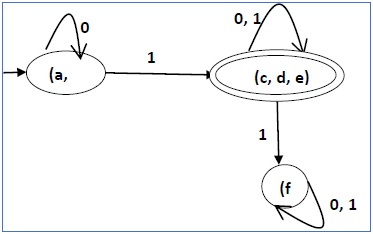
Minimasi DFA menggunakan Teorema Ekuivalensi
Jika X dan Y adalah dua kondisi dalam DFA, kita dapat menggabungkan kedua kondisi ini menjadi {X, Y} jika keduanya tidak dapat dibedakan. Dua keadaan dapat dibedakan, jika ada setidaknya satu string S, sehingga salah satu dari δ (X, S) dan δ (Y, S) menerima dan yang lain tidak menerima. Karenanya, DFA minimal jika dan hanya jika semua negara bagian dapat dibedakan.
Algoritma 3
Step 1 - Semua negara bagian Q dibagi menjadi dua partisi - final states dan non-final states dan dilambangkan dengan P0. Semua status dalam partisi adalah ekuivalen ke- 0 . Ambil counterk dan menginisialisasi dengan 0.
Step 2- Kenaikan k dengan 1. Untuk setiap partisi di P k , bagi negara bagian dalam P k menjadi dua partisi jika dapat dibedakan k. Dua status dalam partisi X dan Y ini dapat dibedakan k jika ada inputS seperti yang δ(X, S) dan δ(Y, S) adalah (k-1) -dibedakan.
Step 3- Jika P k ≠ P k-1 , ulangi Langkah 2, jika tidak lanjutkan ke Langkah 4.
Step 4- Gabungkan set ekivalen ke k dan jadikan status baru DFA yang dikurangi.
Contoh
Mari kita pertimbangkan DFA berikut -

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| Sebuah | b | c |
| b | Sebuah | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
Mari kita terapkan algoritma di atas ke DFA di atas -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Oleh karena itu, P 1 = P 2 .
Ada tiga negara bagian dalam DFA yang dikurangi. DFA yang berkurang adalah sebagai berikut -
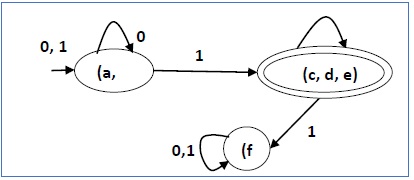
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (f) |
| (f) | (f) | (f) |