Komunikasi Digital - Modulasi Delta
Kecepatan pengambilan sampel sinyal harus lebih tinggi daripada tingkat Nyquist, untuk mencapai pengambilan sampel yang lebih baik. Jika interval pengambilan sampel dalam PCM Diferensial ini dikurangi secara signifikan, perbedaan amplitudo sampel-sampel sangat kecil, seolah-olah perbedaannya adalah1-bit quantization, maka ukuran langkah akan menjadi sangat kecil yaitu, Δ (delta).
Modulasi Delta
Jenis modulasi, di mana laju pengambilan sampel jauh lebih tinggi dan ukuran langkah setelah kuantisasi memiliki nilai yang lebih kecil Δ, modulasi seperti itu disebut sebagai delta modulation.
Fitur Modulasi Delta
Berikut adalah beberapa fitur modulasi delta.
Input yang diambil lebih banyak diambil untuk memanfaatkan sepenuhnya korelasi sinyal.
Desain kuantisasi sederhana.
Urutan masukan jauh lebih tinggi daripada tingkat Nyquist.
Kualitasnya sedang.
Desain modulator dan demodulator sederhana.
Perkiraan bentuk gelombang tangga keluaran.
Ukuran langkahnya sangat kecil, yaitu Δ (delta).
Kecepatan bit dapat ditentukan oleh pengguna.
Ini melibatkan implementasi yang lebih sederhana.
Modulasi Delta adalah bentuk teknik DPCM yang disederhanakan, juga dipandang sebagai 1-bit DPCM scheme. Saat interval pengambilan sampel berkurang, korelasi sinyal akan lebih tinggi.
Modulator Delta
Modulator Delta terdiri dari pengukur 1-bit dan sirkuit penundaan bersama dengan dua sirkuit musim panas. Berikut ini adalah diagram blok modulator delta.
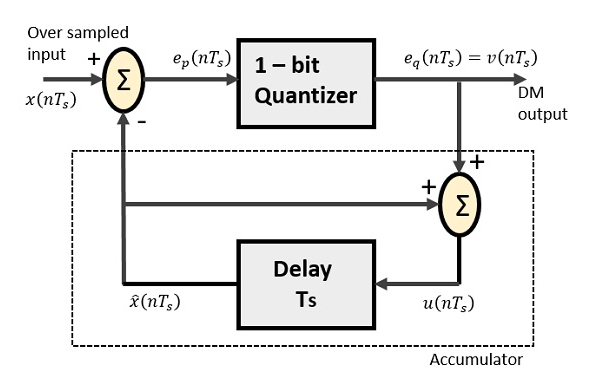
Rangkaian prediktor di DPCM diganti dengan rangkaian penundaan sederhana di DM.
Dari diagram di atas, kami memiliki notasi sebagai -
$ x (nT_ {s}) $ = melebihi input sampel
$ e_ {p} (nT_ {s}) $ = keluaran musim panas dan masukan pembilang
$ e_ {q} (nT_ {s}) $ = keluaran pembilang = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = keluaran rangkaian penundaan
$ u (nT_ {s}) $ = masukan rangkaian penundaan
Dengan menggunakan notasi ini, sekarang kita akan mencoba mencari tahu proses modulasi delta.
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- persamaan 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- persamaan 2
Lebih lanjut,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- persamaan 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
Dimana,
$ \ widehat {x} (nT_ {s}) $ = nilai sebelumnya dari rangkaian penundaan
$ e_ {q} (nT_ {s}) $ = keluaran pembilang = $ v (nT_s) $
Karenanya,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- persamaan 4
Yang berarti,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Dengan asumsi kondisi Akumulasi nol,
$ u (nT_ {s}) = S \ displaystyle \ jumlah \ batas_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ jumlah \ batas_ {j = 1} ^ nv (jT_ {s}) $
--------- persamaan 5
Sekarang, perhatikan itu
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ displaystyle \ jumlah \ batas_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- persamaan 6
Keluaran unit penundaan adalah keluaran Akumulator yang tertinggal oleh satu sampel.
Dari persamaan 5 & 6, kita mendapatkan struktur yang memungkinkan untuk demodulator.
Bentuk gelombang perkiraan kasus tangga akan menjadi keluaran dari modulator delta dengan ukuran langkah sebagai delta (Δ). Kualitas keluaran dari bentuk gelombang sedang.
Delta Demodulator
Demodulator delta terdiri dari low pass filter, summer, dan delay circuit. Sirkuit prediktor dihilangkan di sini dan karenanya tidak ada input yang diasumsikan diberikan ke demodulator.
Berikut adalah diagram demodulator delta.
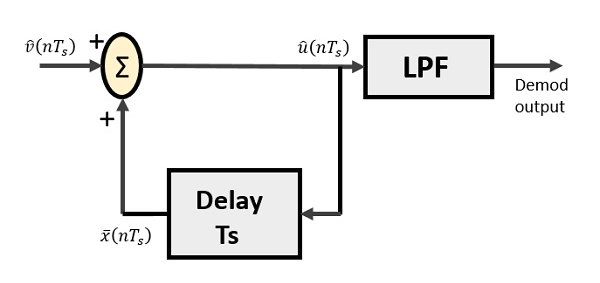
Dari diagram di atas, kami memiliki notasi sebagai -
$ \ widehat {v} (nT_ {s}) $ adalah contoh masukan
$ \ widehat {u} (nT_ {s}) $ adalah keluaran musim panas
$ \ bar {x} (nT_ {s}) $ adalah keluaran yang tertunda
Urutan biner akan diberikan sebagai masukan ke demodulator. Keluaran perkiraan kotak-tangga diberikan ke LPF.
Filter akses rendah digunakan karena berbagai alasan, tetapi alasan utamanya adalah penghapusan noise untuk sinyal out-of-band. Kesalahan ukuran langkah yang mungkin terjadi pada pemancar disebutgranular noise, yang dihilangkan di sini. Jika tidak ada gangguan, maka keluaran modulator sama dengan masukan demodulator.
Keuntungan DM Dibandingkan DPCM
Penghitung 1-bit
Desain modulator dan demodulator yang sangat mudah
Namun, ada beberapa gangguan di DM.
Slope Over load distortion (saat Δ kecil)
Kebisingan granular (kapan Δ besar)
Adaptive Delta Modulation (ADM)
Dalam modulasi digital, kami menemukan masalah tertentu dalam menentukan ukuran langkah, yang mempengaruhi kualitas gelombang keluaran.
Ukuran langkah yang lebih besar diperlukan di kemiringan curam sinyal modulasi dan ukuran langkah yang lebih kecil diperlukan jika pesan memiliki kemiringan kecil. Detail menit terlewatkan dalam prosesnya. Jadi, akan lebih baik jika kita dapat mengontrol penyesuaian ukuran langkah, sesuai dengan kebutuhan kita untuk mendapatkan pengambilan sampel dengan cara yang diinginkan. Ini adalah konsepAdaptive Delta Modulation.
Berikut adalah diagram blok dari Adaptive delta modulator.
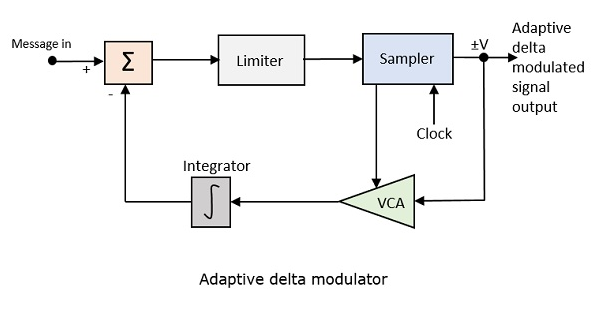
Gain dari penguat yang dikendalikan tegangan disesuaikan dengan sinyal keluaran dari sampler. Penguatan penguat menentukan ukuran langkah dan keduanya proporsional.
ADM menghitung selisih antara nilai sampel saat ini dan nilai prediksi sampel berikutnya. Ini menggunakan tinggi langkah variabel untuk memprediksi nilai berikutnya, untuk reproduksi yang tepat dari nilai yang berubah cepat.