Teorema Pengkodean Sumber
Kode yang dihasilkan oleh sumber diskrit tanpa memori, harus diwakili secara efisien, yang merupakan masalah penting dalam komunikasi. Untuk mewujudkannya, ada kata kode, yang mewakili kode sumber ini.
Misalnya, dalam telegrafi, kami menggunakan kode Morse, di mana huruf dilambangkan dengan Marks dan Spaces. Jika surat ituE dianggap, yang paling sering digunakan, dilambangkan dengan “.” Padahal surat itu Q yang jarang digunakan, dilambangkan dengan “--.-”
Mari kita lihat diagram blok.
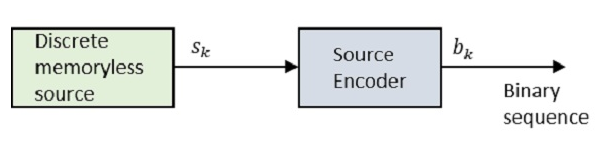
Dimana Sk adalah keluaran dari sumber tanpa memori diskrit dan bk adalah keluaran dari encoder sumber yang diwakili oleh 0s dan 1s.
Urutan yang dikodekan sedemikian rupa sehingga mudah didekodekan di penerima.
Mari kita asumsikan bahwa sumber memiliki alfabet dengan k simbol yang berbeda dan itu kth simbol Sk terjadi dengan probabilitas Pk, dimana k = 0, 1…k-1.
Biarkan kata kode biner ditugaskan untuk simbol Sk, oleh encoder yang memiliki panjang lk, diukur dalam bit.
Oleh karena itu, kami mendefinisikan panjang kata kode rata-rata L dari encoder sumber sebagai
$$ \ overline {L} = \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p_kl_k $$
L mewakili jumlah rata-rata bit per simbol sumber
Jika $ L_ {min} = \: minimum \: mungkin \: nilai \: dari \: \ overline {L} $
Kemudian coding efficiency dapat didefinisikan sebagai
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
Dengan $ \ overline {L} \ geq L_ {min} $ kita akan memiliki $ \ eta \ leq 1 $
Namun, encoder sumber dianggap efisien jika $ \ eta = 1 $
Untuk ini, nilai $ L_ {min} $ harus ditentukan.
Mari kita lihat definisi, “Diberikan sumber tanpa memori diskrit dari entropi $ H (\ delta) $, rata-rata panjang kata kodeL untuk pengkodean sumber apa pun dibatasi sebagai $ \ overline {L} \ geq H (\ delta) $. "
Dengan kata yang lebih sederhana, kata kode (contoh: kode Morse untuk kata ANTRIAN adalah -.- ..-. ..-.) Selalu lebih besar dari atau sama dengan kode sumber (misalnya ANTRIAN). Artinya, simbol pada kata kode lebih besar dari atau sama dengan huruf pada kode sumber.
Karenanya dengan $ L_ {min} = H (\ delta) $, efisiensi encoder sumber dalam hal Entropi $ H (\ delta) $ dapat ditulis sebagai
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Teorema pengkodean sumber ini disebut sebagai noiseless coding theoremkarena ini menetapkan pengkodean bebas kesalahan. Itu juga disebut sebagaiShannon’s first theorem.