Fuzzy Logic - Teori Himpunan

Himpunan fuzzy dapat dianggap sebagai perluasan dan penyederhanaan berlebihan dari himpunan klasik. Ini dapat dipahami dengan baik dalam konteks keanggotaan yang ditetapkan. Pada dasarnya memungkinkan keanggotaan parsial yang berarti mengandung unsur-unsur yang memiliki tingkat keanggotaan yang berbeda-beda di himpunan. Dari sini, kita dapat memahami perbedaan antara himpunan klasik dan himpunan fuzzy. Himpunan klasik berisi elemen yang memenuhi properti keanggotaan yang tepat sedangkan himpunan fuzzy berisi elemen yang memenuhi properti keanggotaan yang tidak tepat.

Konsep Matematika

Himpunan fuzzy $ \ widetilde {A} $ dalam semesta informasi $ U $ dapat didefinisikan sebagai himpunan pasangan terurut dan secara matematis dapat direpresentasikan sebagai -

$$ \ widetilde {A} = \ kiri \ {\ kiri (y, \ mu _ {\ widetilde {A}} \ kiri (y \ kanan) \ kanan) | y \ di U \ kanan \} $$

Di sini $ \ mu _ {\ widetilde {A}} \ left (y \ right) $ = derajat keanggotaan $ y $ in \ widetilde {A}, mengasumsikan nilai dalam rentang 0 hingga 1, yaitu $ \ mu _ {\ widetilde {A}} (y) \ di \ kiri [0,1 \ kanan] $.

Representasi himpunan fuzzy

Sekarang mari kita pertimbangkan dua kasus semesta informasi dan memahami bagaimana himpunan fuzzy dapat direpresentasikan.

Kasus 1

Ketika semesta informasi $ U $ diskrit dan terbatas -

$$ \ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left (y_1 \ kanan)} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ kiri (y_2 \ kanan)} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ kiri (y_3 \ kanan)} {y_3} + ... \ kanan \} $$

$ = \ kiri \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ kiri (y_i \ kanan)} {y_i} \ kanan \} $

Kasus 2

Ketika semesta informasi $ U $ kontinu dan tak terbatas -

$$ \ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left (y \ kanan)} {y} \ kanan \} $$

Dalam representasi di atas, simbol penjumlahan mewakili kumpulan setiap elemen.

Operasi pada Set Fuzzy

Memiliki dua himpunan fuzzy $ \ widetilde {A} $ dan $ \ widetilde {B} $, semesta informasi $ U $ dan sebuah elemen alam semesta, relasi berikut mengungkapkan operasi gabungan, perpotongan dan komplemen pada himpunan fuzzy.

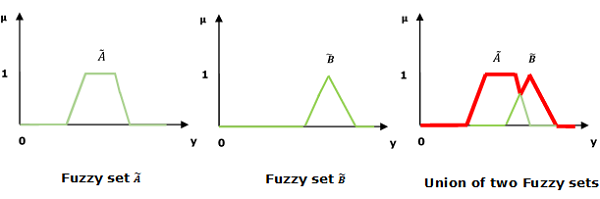
Union / Fuzzy 'OR'

Mari kita simak representasi berikut untuk memahami bagaimana Union/Fuzzy ‘OR’ hubungan bekerja -

$$ \ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ kiri (y \ kanan) = \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$

Di sini ∨ mewakili operasi 'maks'.

Persimpangan / Fuzzy 'AND'

Mari kita simak representasi berikut untuk memahami bagaimana Intersection/Fuzzy ‘AND’ hubungan bekerja -

$$ \ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ kiri (y \ kanan) = \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$

Di sini ∧ mewakili operasi 'min'.

Komplemen / Fuzzy 'NOT'

Mari kita simak representasi berikut untuk memahami bagaimana Complement/Fuzzy ‘NOT’ hubungan bekerja -

$$ \ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ kiri (y \ kanan) \ quad y \ dalam U $$

Properti Set Fuzzy

Mari kita bahas berbagai properti himpunan fuzzy.

Properti Komutatif

Memiliki dua set fuzzy $ \ widetilde {A} $ dan $ \ widetilde {B} $, properti ini menyatakan -

$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$

$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $$

Properti Asosiatif

Memiliki tiga set fuzzy $ \ widetilde {A} $, $ \ widetilde {B} $ dan $ \ widetilde {C} $, properti ini menyatakan -

$$ (\ widetilde {A} \ cup \ left \ widetilde {B}) \ cup \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ kanan) \ cup \ widetilde {C}) $$

$$ (\ widetilde {A} \ cap \ left \ widetilde {B}) \ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right \ cap \ widetilde { C}) $$

Properti Distributif

Memiliki tiga set fuzzy $ \ widetilde {A} $, $ \ widetilde {B} $ dan $ \ widetilde {C} $, properti ini menyatakan -

$$ \ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ kanan) \ cap \ kiri (\ widetilde {A} \ cup \ widetilde {C} \ kanan) $$

$$ \ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde {B} \ kanan) \ cup \ kiri (\ widetilde {A} \ cap \ widetilde {C} \ kanan) $$

Properti Idempotensi

Untuk himpunan fuzzy $ \ widetilde {A} $, properti ini menyatakan -

$$ \ widetilde {A} \ cup \ widetilde {A} = \ widetilde {A} $$

$$ \ widetilde {A} \ cap \ widetilde {A} = \ widetilde {A} $$

Properti Identitas

Untuk himpunan fuzzy $ \ widetilde {A} $ dan himpunan universal $ U $, properti ini menyatakan -

$$ \ widetilde {A} \ cup \ varphi = \ widetilde {A} $$

$$ \ widetilde {A} \ cap U = \ widetilde {A} $$

$$ \ widetilde {A} \ cap \ varphi = \ varphi $$

$$ \ widetilde {A} \ cup U = U $$

Properti Transitif

Memiliki tiga set fuzzy $ \ widetilde {A} $, $ \ widetilde {B} $ dan $ \ widetilde {C} $, properti ini menyatakan -

$$ If \: \ widetilde {A} \ subseteq \ widetilde {B} \ subseteq \ widetilde {C}, \: then \: \ widetilde {A} \ subseteq \ widetilde {C} $$

Properti Involusi

Untuk himpunan fuzzy $ \ widetilde {A} $, properti ini menyatakan -

$$ \ overline {\ overline {\ widetilde {A}}} = \ widetilde {A} $$

Hukum De Morgan

Undang-undang ini memainkan peran penting dalam membuktikan tautologi dan kontradiksi. Hukum ini menyatakan -

$$ \ overline {{\ widetilde {A} \ cap \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cup \ overline {\ widetilde {B}} $$

$$ \ overline {{\ widetilde {A} \ cup \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cap \ overline {\ widetilde {B}} $$