Algoritma Regresi - Regresi Linier
Pengantar Regresi Linier
Regresi linier dapat didefinisikan sebagai model statistik yang menganalisis hubungan linier antara variabel dependen dengan kumpulan variabel independen tertentu. Hubungan linier antar variabel berarti ketika nilai satu atau lebih variabel independen akan berubah (naik atau turun), nilai variabel dependen juga akan berubah sesuai (naik atau turun).
Secara matematis hubungan tersebut dapat direpresentasikan dengan bantuan persamaan berikut -
Y = mX + b
Di sini, Y adalah variabel dependen yang kami coba prediksi
X adalah variabel dependen yang kami gunakan untuk membuat prediksi.
m adalah slop dari garis regresi yang merepresentasikan pengaruh X terhadap Y
b adalah sebuah konstanta, yang dikenal sebagai titik potong-Y. Jika X = 0, Y akan sama dengan b.
Selanjutnya hubungan linier tersebut dapat bersifat positif atau negatif seperti yang dijelaskan di bawah ini -
Hubungan Linear Positif
Hubungan linier akan disebut positif jika variabel independen dan dependen meningkat. Ini dapat dipahami dengan bantuan grafik berikut -

Hubungan Linear Negatif
Hubungan linier akan disebut positif jika independen meningkat dan variabel dependen menurun. Ini dapat dipahami dengan bantuan grafik berikut -

Jenis-jenis Regresi Linier
Regresi linier adalah dari dua jenis berikut -
- Regresi Linier Sederhana
- Regresi Linear Berganda
Regresi Linier Sederhana (SLR)
Ini adalah versi paling dasar dari regresi linier yang memprediksi respons menggunakan fitur tunggal. Asumsi dalam SLR adalah bahwa kedua variabel tersebut berhubungan secara linier.
Implementasi Python
Kami dapat mengimplementasikan SLR dengan Python dalam dua cara, satu adalah dengan menyediakan dataset Anda sendiri dan yang lainnya adalah dengan menggunakan dataset dari pustaka python scikit-learn.
Example 1 - Dalam contoh implementasi Python berikut, kami menggunakan dataset kami sendiri.
Pertama, kita akan mulai dengan mengimpor paket yang diperlukan sebagai berikut -
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltSelanjutnya, tentukan fungsi yang akan menghitung nilai penting untuk SLR -
def coef_estimation(x, y):Baris skrip berikut akan memberikan jumlah pengamatan n -
n = np.size(x)Rata-rata vektor x dan y dapat dihitung sebagai berikut -
m_x, m_y = np.mean(x), np.mean(y)Kita dapat menemukan deviasi silang dan deviasi tentang x sebagai berikut -
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xSelanjutnya, koefisien regresi yaitu b dapat dihitung sebagai berikut -
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Selanjutnya, kita perlu menentukan fungsi yang akan memplot garis regresi serta akan memprediksi vektor respons -
def plot_regression_line(x, y, b):Baris skrip berikut akan memplot titik-titik aktual sebagai plot pencar -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Baris skrip berikut akan memprediksi vektor respons -
y_pred = b[0] + b[1]*xBaris skrip berikut akan memplot garis regresi dan akan memberi label padanya -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Terakhir, kita perlu mendefinisikan fungsi main () untuk menyediakan dataset dan memanggil fungsi yang kita definisikan di atas -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Keluaran
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788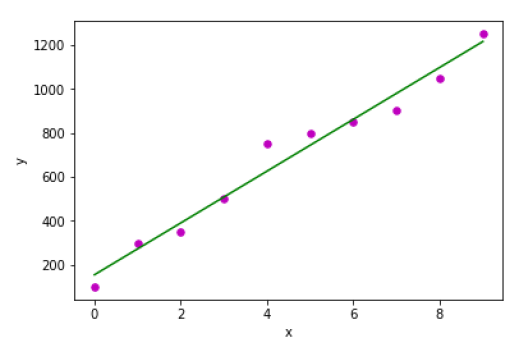
Example 2 - Dalam contoh implementasi Python berikut, kami menggunakan dataset diabetes dari scikit-learn.
Pertama, kita akan mulai dengan mengimpor paket yang diperlukan sebagai berikut -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreSelanjutnya, kita akan memuat dataset diabetes dan membuat objeknya -
diabetes = datasets.load_diabetes()Saat kami menerapkan SLR, kami hanya akan menggunakan satu fitur sebagai berikut -
X = diabetes.data[:, np.newaxis, 2]Selanjutnya, kita perlu membagi data menjadi set pelatihan dan pengujian sebagai berikut -
X_train = X[:-30]
X_test = X[-30:]Selanjutnya, kita perlu membagi target menjadi set pelatihan dan pengujian sebagai berikut -
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Nah, untuk melatih model tersebut kita perlu membuat objek regresi linier sebagai berikut -
regr = linear_model.LinearRegression()Selanjutnya, latih model menggunakan set pelatihan sebagai berikut -
regr.fit(X_train, y_train)Selanjutnya, buat prediksi menggunakan set pengujian sebagai berikut -
y_pred = regr.predict(X_test)Selanjutnya, kami akan mencetak beberapa koefisien seperti MSE, skor Varians, dll. Sebagai berikut -
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Sekarang, plot hasilnya sebagai berikut -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Keluaran
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Regresi Linier Berganda (MLR)
Ini adalah perluasan dari regresi linier sederhana yang memprediksi respons menggunakan dua fitur atau lebih. Secara matematis kita dapat menjelaskannya sebagai berikut -
Pertimbangkan dataset yang memiliki n observasi, fitur p yaitu variabel independen dan y sebagai salah satu respon yaitu variabel dependen, garis regresi untuk fitur p dapat dihitung sebagai berikut -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$Di sini, h (x i ) adalah nilai respon yang diprediksi dan b 0 , b 1 , b 2 …, b p adalah koefisien regresi.
Model Regresi Linier Berganda selalu memasukkan kesalahan dalam data yang dikenal sebagai kesalahan sisa yang mengubah perhitungan sebagai berikut -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$Kita juga bisa menuliskan persamaan di atas sebagai berikut -
$$ y_ {i} = h (x_ {i}) + e_ {i} \: atau \: e_ {i} = y_ {i} - h (x_ {i}) $$Implementasi Python
dalam contoh ini, kami akan menggunakan dataset perumahan Boston dari scikit learn -
Pertama, kita akan mulai dengan mengimpor paket yang diperlukan sebagai berikut -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsSelanjutnya, muat dataset sebagai berikut -
boston = datasets.load_boston(return_X_y=False)Baris skrip berikut akan mendefinisikan matriks fitur, X dan vektor respons, Y -
X = boston.data
y = boston.targetSelanjutnya, bagi set data menjadi set pelatihan dan pengujian sebagai berikut -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Contoh
Sekarang, buat objek regresi linier dan latih model sebagai berikut -
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Keluaran
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
Asumsi
Berikut ini adalah beberapa asumsi mengenai dataset yang dibuat dengan model Regresi Linier -
Multi-collinearity- Model regresi linier mengasumsikan bahwa ada sangat sedikit atau tidak ada multikolinearitas dalam data. Pada dasarnya, multi-collinearity terjadi ketika variabel atau fitur independen memiliki ketergantungan di dalamnya.
Auto-correlation- Asumsi lain Model regresi linier mengasumsikan bahwa terdapat sangat sedikit atau tidak ada korelasi otomatis dalam data. Pada dasarnya, korelasi otomatis terjadi ketika ada ketergantungan antara kesalahan residual.
Relationship between variables - Model regresi linier mengasumsikan bahwa hubungan antara variabel respon dan fitur harus linier.