Mencari luas segitiga siku-siku atau persegi panjang yang sesuai
Area of a right triangle
Pertimbangkan persegi panjang dengan satuan panjang l dan lebar w satuan. Mari kita menggambar diagonal dan memotong persegi panjang. Mari kita juga memotong diagonal untuk membentuk dua segitiga siku-siku.
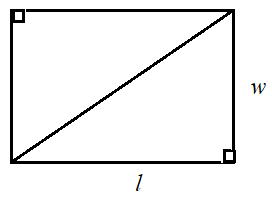
Diketahui bahwa kedua segitiga siku-siku tersebut memiliki luas dan ukuran yang sama serta kongruen. Jadi luas setiap segitiga siku-siku adalah setengah luas persegi panjang.
Luas segitiga siku-siku = $ \ frac {1} {2} $ luas persegi panjang = $ \ frac {1} {2} $ l × w
Panjang l persegi panjang adalah alas b segitiga siku-siku dan lebar w persegi panjang adalah tinggi h segitiga siku-siku.
So area of right triangle = $\mathbf{\frac{1}{2}}$ l × w = $\mathbf{\frac{1}{2}}$ b × h
Luas segitiga siku-siku adalah setengah luas persegi panjang yang bersesuaian
Temukan luas segitiga siku-siku berikut dan persegi panjang yang sesuai.
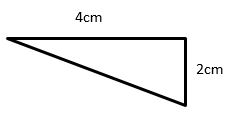
Larutan
Step 1:
Luas Segitiga Siku-siku = $ \ frac {1} {2} $ × b × h; b = alas = 4; h = tinggi = 2
Step 2:
Luas Segitiga Siku- siku = $ \ frac {1} {2} $ × 4 × 2 = 4 cm persegi
Luas persegi panjang yang bersesuaian = b × t = 4 × 2 = 8 cm persegi
Temukan luas segitiga siku-siku berikut dan persegi panjang yang sesuai.
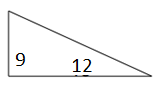
Larutan
Step 1:
Luas Segitiga Siku-siku = $ \ frac {1} {2} $ × b × h; b = alas = 12; h = tinggi = 9
Step 2:
Luas Segitiga Siku- siku = $ \ frac {1} {2} $ × 12 × 9 = 54 satuan persegi
Luas persegi panjang yang sesuai = b × t = 12 × 9 = 108 persegi