SciPy - Spasial

Itu scipy.spatial package dapat menghitung Triangulasi, Diagram Voronoi, dan Convex Hulls dari sekumpulan titik, dengan memanfaatkan Qhull library. Apalagi mengandungKDTree implementations untuk kueri titik tetangga terdekat dan utilitas untuk penghitungan jarak dalam berbagai metrik.

Triangulasi Delaunay

Mari kita pahami apa itu Delaunay Triangulations dan bagaimana penggunaannya di SciPy.

Apa itu Triangulasi Delaunay?

Dalam matematika dan geometri komputasi, triangulasi Delaunay untuk himpunan tertentu P titik diskrit dalam bidang adalah triangulasi DT(P) sedemikian rupa sehingga tidak ada gunanya P berada di dalam lingkaran sirkit segitiga apa pun di DT (P).

Kita dapat menghitungnya melalui SciPy. Mari kita perhatikan contoh berikut.

from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

Program di atas akan menghasilkan keluaran sebagai berikut.

Coplanar Points

Mari kita pahami apa itu Coplanar Points dan bagaimana penggunaannya di SciPy.

Apa itu Poin Coplanar?

Titik coplanar adalah tiga titik atau lebih yang terletak pada bidang yang sama. Ingatlah bahwa bidang adalah permukaan datar, yang memanjang tanpa ujung ke segala arah. Biasanya ini ditampilkan dalam buku teks matematika sebagai gambar empat sisi.

Mari kita lihat bagaimana kita dapat menemukannya menggunakan SciPy. Mari kita perhatikan contoh berikut.

from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar

Program di atas akan menghasilkan keluaran sebagai berikut.

array([[4, 0, 3]], dtype = int32)

Artinya titik 4 berada di dekat segitiga 0 dan titik 3, tetapi tidak termasuk dalam triangulasi tersebut.

Lambung cembung

Mari kita pahami apa itu convex hull dan bagaimana penggunaannya di SciPy.

Apa itu Convex Hulls?

Dalam matematika, file convex hull atau convex envelope dari satu set titik X di bidang Euclidean atau di ruang Euclidean (atau, lebih umum, dalam ruang affine di atas real) adalah yang terkecil convex set yang berisi X.

Mari kita perhatikan contoh berikut untuk memahaminya secara detail.

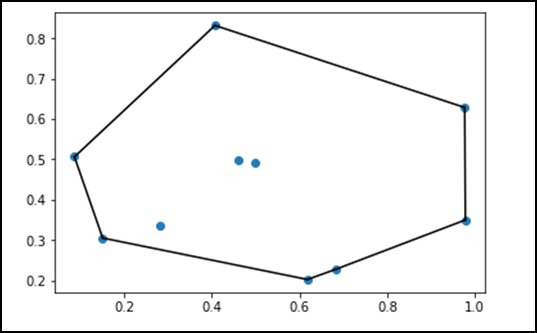
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

Program di atas akan menghasilkan keluaran sebagai berikut.