Introduzione grammaticale senza contesto
Definition - Una grammatica libera dal contesto (CFG) costituita da un insieme finito di regole grammaticali è quadrupla (N, T, P, S) dove
N è un insieme di simboli non terminali.
T è un insieme di terminali dove N ∩ T = NULL.
P è un insieme di regole, P: N → (N ∪ T)*, vale a dire, il lato sinistro della regola di produzione P ha un contesto corretto o un contesto sinistro.
S è il simbolo di inizio.
Example
- La grammatica ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
- La grammatica ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- La grammatica ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generazione dell'albero di derivazione
Un albero di derivazione o albero sintetico è un albero radicato ordinato che rappresenta graficamente le informazioni semantiche una stringa derivata da una grammatica libera dal contesto.
Tecnica di rappresentazione
Root vertex - Deve essere contrassegnato dal simbolo di avvio.
Vertex - Contrassegnato da un simbolo non terminale.
Leaves - Contrassegnato da un simbolo di terminale o ε.
Se S → x 1 x 2 …… x n è una regola di produzione in un CFG, l'albero di analisi / albero di derivazione sarà il seguente:

Esistono due diversi approcci per disegnare un albero di derivazione:
Top-down Approach −
Inizia con il simbolo iniziale S
Scende alle foglie degli alberi usando le produzioni
Bottom-up Approach −
Inizia dalle foglie degli alberi
Procede verso l'alto fino alla radice che è il simbolo iniziale S
Derivazione o resa di un albero
La derivazione o la resa di un albero sintetico è la stringa finale ottenuta concatenando le etichette delle foglie dell'albero da sinistra a destra, ignorando i Nulli. Tuttavia, se tutte le foglie sono Null, la derivazione è Null.
Example
Sia un CFG {N, T, P, S}
N = {S}, T = {a, b}, simbolo iniziale = S, P = S → SS | aSb | ε
Una derivazione del CFG sopra è "abaabb"
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Forma sentenziale e albero di derivazione parziale
Un albero di derivazione parziale è un sottoalbero di un albero di derivazione / albero sintetico in modo tale che tutti i suoi figli siano nel sottoalbero o nessuno di loro si trovi nel sottoalbero.
Example
Se in qualsiasi CFG le produzioni sono -
S → AB, A → aaA | ε, B → Bb | ε
l'albero di derivazione parziale può essere il seguente:
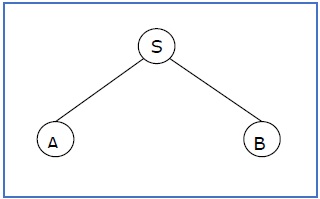
Se un albero di derivazione parziale contiene la radice S, viene chiamato a sentential form. Il sottoalbero di cui sopra è anche in forma sentenziale.
Derivazione più a sinistra e più a destra di una stringa
Leftmost derivation - Una derivazione più a sinistra si ottiene applicando la produzione alla variabile più a sinistra in ogni passaggio.
Rightmost derivation - Una derivazione più a destra si ottiene applicando la produzione alla variabile più a destra in ogni passaggio.
Example
Lascia che qualsiasi insieme di regole di produzione in un CFG sia
X → X + X | X * X | X | un
su un alfabeto {a}.
La derivazione più a sinistra per la stringa "a+a*a" può essere -
X → X + X → a + X → a + X * X → a + a * X → a + a * a
La derivazione graduale della stringa sopra è mostrata come di seguito:

La derivazione più a destra per la stringa precedente "a+a*a" può essere -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
La derivazione graduale della stringa sopra è mostrata come di seguito:

Grammatiche ricorsive sinistra e destra
In una grammatica priva di contesto G, se c'è una produzione nella forma X → Xa dove X è un non terminale e ‘a’ è una stringa di terminali, si chiama a left recursive production. La grammatica che ha una produzione ricorsiva sinistra è chiamata aleft recursive grammar.
E se in una grammatica priva di contesto G, se c'è una produzione è nella forma X → aX dove X è un non terminale e ‘a’ è una stringa di terminali, si chiama a right recursive production. La grammatica che ha una produzione ricorsiva corretta è chiamata aright recursive grammar.