Automa finito non deterministico
In NDFA, per un particolare simbolo di input, la macchina può spostarsi in qualsiasi combinazione degli stati nella macchina. In altre parole, non è possibile determinare lo stato esatto in cui si sposta la macchina. Quindi, si chiamaNon-deterministic Automaton. Poiché ha un numero finito di stati, la macchina viene chiamataNon-deterministic Finite Machine o Non-deterministic Finite Automaton.
Definizione formale di un NDFA
Un NDFA può essere rappresentato da una tupla di 5 (Q, ∑, δ, q 0 , F) dove -
Q è un insieme finito di stati.
∑ è un insieme finito di simboli chiamati alfabeti.
δè la funzione di transizione dove δ: Q × ∑ → 2 Q
(Qui è stato preso il power set di Q (2 Q ) perché in caso di NDFA, da uno stato, la transizione può avvenire a qualsiasi combinazione di stati Q)
q0è lo stato iniziale da cui viene elaborato qualsiasi input (q 0 ∈ Q).
F è un insieme di stati finali di Q (F ⊆ Q).
Rappresentazione grafica di un NDFA: (come DFA)
Un NDFA è rappresentato da digrafi chiamati diagramma di stato.
- I vertici rappresentano gli stati.
- Gli archi etichettati con un alfabeto di input mostrano le transizioni.
- Lo stato iniziale è indicato da un singolo arco in entrata vuoto.
- Lo stato finale è indicato da doppi cerchi.
Example
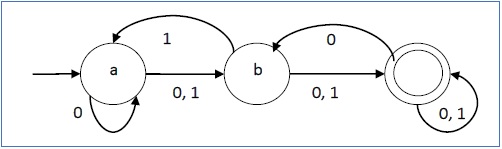
Sia un automa finito non deterministico →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
La funzione di transizione δ come mostrato di seguito -
| Stato attuale | Stato successivo per ingresso 0 | Stato successivo per ingresso 1 |
|---|---|---|
| un | a, b | b |
| b | c | corrente alternata |
| c | avanti Cristo | c |
La sua rappresentazione grafica sarebbe la seguente:
DFA vs NDFA
La tabella seguente elenca le differenze tra DFA e NDFA.
| DFA | NDFA |
|---|---|
| La transizione da uno stato è a un singolo particolare stato successivo per ogni simbolo di ingresso. Quindi è chiamato deterministico . | La transizione da uno stato può avvenire a più stati successivi per ogni simbolo di ingresso. Quindi è chiamato non deterministico . |
| Le transizioni di stringhe vuote non vengono visualizzate in DFA. | NDFA consente transizioni di stringhe vuote. |
| Il backtracking è consentito in DFA | In NDFA, il backtracking non è sempre possibile. |
| Richiede più spazio. | Richiede meno spazio. |
| Una stringa viene accettata da un DFA, se transita in uno stato finale. | Una stringa viene accettata da un NDFA, se almeno una di tutte le possibili transizioni termina in uno stato finale. |
Accettori, classificatori e trasduttori
Accettatore (Riconoscitore)
Un automa che calcola una funzione booleana è chiamato un acceptor. Tutti gli stati di un accettore accettano o rifiutano gli input forniti.
Classificatore
UN classifier ha più di due stati finali e fornisce un singolo output quando termina.
Trasduttore
Un automa che produce output in base all'input corrente e / o allo stato precedente è chiamato a transducer. I trasduttori possono essere di due tipi:
Mealy Machine - L'uscita dipende sia dallo stato corrente che dall'ingresso corrente.
Moore Machine - L'uscita dipende solo dallo stato corrente.
Accettabilità da parte di DFA e NDFA
Una stringa viene accettata da un DFA / NDFA se e solo se il DFA / NDFA che inizia dallo stato iniziale termina in uno stato di accettazione (uno degli stati finali) dopo aver letto interamente la stringa.
Una stringa S è accettata da un DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
La lingua L accettato da DFA / NDFA è
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Una stringa S ′ non è accettata da un DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
La lingua L ′ non accettata da DFA / NDFA (Complemento della lingua accettata L) è
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Consideriamo il DFA mostrato nella Figura 1.3. Da DFA è possibile derivare le stringhe accettabili.

Stringhe accettate dal DFA precedente: {0, 00, 11, 010, 101, ...........}
Stringhe non accettate dal DFA precedente: {1, 011, 111, ........}