Circuiti aritmetici digitali
In questo capitolo, discutiamo dei circuiti aritmetici di base come il sommatore binario e il sottrattore binario. Questi circuiti possono essere utilizzati con valori binari 0 e 1.
Sommatore binario
L'operazione aritmetica più elementare è l'addizione. Il circuito, che esegue l'addizione di due numeri binari, è noto comeBinary adder. Per prima cosa, implementiamo un sommatore, che esegue l'aggiunta di due bit.
Mezzo sommatore
Half adder è un circuito combinatorio, che esegue l'aggiunta di due numeri binari di cui A e B. single bit. Produce due uscite somma, S & carry, C.
Il Truth table di Half adder è mostrato di seguito.
| Ingressi | Uscite | ||
|---|---|---|---|
| UN | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Quando facciamo l'addizione di due bit, la somma risultante può avere valori compresi tra 0 e 2 in decimale. Possiamo rappresentare le cifre decimali 0 e 1 con un singolo bit in binario. Ma non possiamo rappresentare la cifra decimale 2 con un singolo bit in binario. Quindi, abbiamo bisogno di due bit per rappresentarlo in binario.
Somma, S è il bit meno significativo e riporto, C è il bit più significativo della somma risultante. Per le prime tre combinazioni di input, carry, C è zero e il valore di S sarà zero o uno in base anumber of onespresente agli ingressi. Ma, per l'ultima combinazione di input, carry, C è uno e sum, S è zero, poiché la somma risultante è due.
Dalla tabella Truth, possiamo scrivere direttamente il file Boolean functions per ogni uscita come
$$ S = A \ oplus B $$
$ C = AB $
Possiamo implementare le funzioni di cui sopra con porta Ex-OR a 2 ingressi e porta AND a 2 ingressi. Ilcircuit diagram di Half adder è mostrato nella figura seguente.

Nel circuito sopra, una porta Ex-OR a due ingressi e una porta AND a due ingressi producono rispettivamente somma, S e riporto, C. Pertanto, Half-adder esegue l'aggiunta di due bit.
Sommatore completo
Il sommatore completo è un circuito combinatorio, che esegue il addition of three bitsA, B e C in . Dove, A e B sono i due bit significativi paralleli e C in è il bit di riporto, che viene generato dalla fase precedente. Questo sommatore completo produce anche due uscite somma, S & carry, C out , che sono simili a Half sommatore.
Il Truth table di Full adder è mostrato di seguito.
| Ingressi | Uscite | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Quando aggiungiamo tre bit, la somma risultante può avere valori compresi tra 0 e 3 in decimale. Possiamo rappresentare le cifre decimali 0 e 1 con un singolo bit in binario. Ma non possiamo rappresentare le cifre decimali 2 e 3 con un singolo bit in binario. Quindi, abbiamo bisogno di due bit per rappresentare quelle due cifre decimali in binario.
Somma, S è il bit meno significativo e porta C out è il bit più significativo della somma risultante. È facile riempire i valori degli output per tutte le combinazioni di input nella tabella della verità. Basta contare il filenumber of onespresente agli ingressi e scrive il numero binario equivalente sulle uscite. Se C in è uguale a zero, la tabella di verità del sommatore completo è uguale a quella della tabella di verità del sommatore mezzo.
Otterremo quanto segue Boolean functions per ogni uscita dopo la semplificazione.
$$ S = A \ oplus B \ oplus C_ {in} $$
$ c_ {out} = AB + \ left (A \ oplus B \ right) c_ {in} $
La somma, S è uguale a uno, quando numero dispari di quelli presenti agli ingressi. Sappiamo che la porta Ex-OR produce un output, che è una funzione dispari. Quindi, possiamo usare due porte Ex-OR a 2 ingressi o una porta Ex-OR a 3 ingressi per produrre la somma, S. Possiamo implementare il carry, C out utilizzando due porte AND a 2 ingressi e una porta OR. Ilcircuit diagram di Full adder è mostrato nella figura seguente.
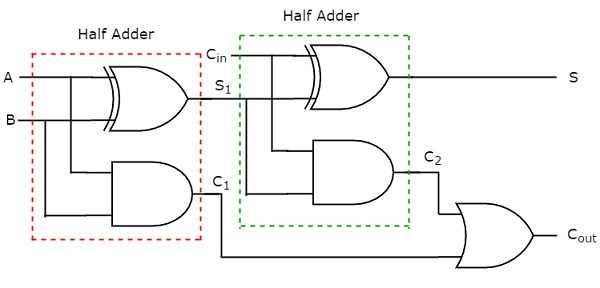
Questo sommatore è chiamato come Full adderperché per implementare un sommatore completo, abbiamo bisogno di due sommatori Half e un cancello OR. Se C in è zero, allora Full adder diventa Half adder. Possiamo verificarlo facilmente dallo schema elettrico sopra o dalle funzioni booleane delle uscite di Full sommatore.
Sommatore binario a 4 bit
Il sommatore binario a 4 bit esegue il addition of two 4-bit numbers. Siano i numeri binari a 4 bit, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ e $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Possiamo implementare il sommatore binario a 4 bit in uno dei due modi seguenti.
Usa un mezzo sommatore per fare l'aggiunta di due bit meno significativi e tre sommatori completi per fare l'aggiunta di tre bit significativi più alti.
Utilizzare quattro sommatori completi per uniformità. Poiché il riporto iniziale C in è zero, il sommatore completo che viene utilizzato per aggiungere i bit meno significativi diventa Half sommatore.
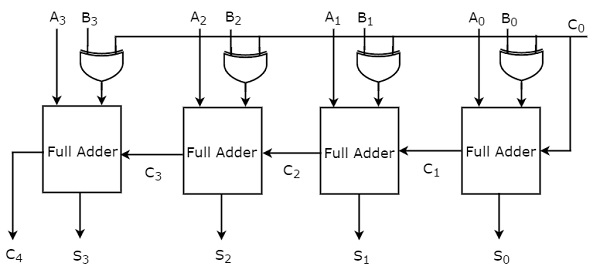
Per il momento abbiamo considerato un secondo approccio. Ilblock diagram di sommatore binario a 4 bit è mostrato nella figura seguente.

Qui, i 4 sommatori completi sono in cascata. Ogni Full adder riceve i rispettivi bit di due ingressi paralleli A e B. L'output di carry di un Full adder sarà l'input di carry del successivo Full adder di ordine superiore. Questo sommatore binario a 4 bit produce la somma risultante con al massimo 5 bit. Quindi, eseguire l'ultima fase Il sommatore completo sarà il MSB.
In questo modo, possiamo implementare qualsiasi sommatore binario di ordine superiore semplicemente sovrapponendo il numero richiesto di sommatori completi. Questo sommatore binario è anche chiamato comeripple carry (binary) adder perché il riporto si propaga (increspature) da uno stadio a quello successivo.
Sottrattore binario
Il circuito, che esegue la sottrazione di due numeri binari, è noto come Binary subtractor. Possiamo implementare il sottrattore binario seguendo due metodi.
- Sottrattori completi a cascata
- Metodo del complemento di 2
Nel primo metodo, otterremo un sottrattore binario a n bit sovrapponendo 'n' sottrattori completi. Quindi, prima puoi implementare Half sottractor e Full sottractor, simili a Half adder e Full adder. Quindi, puoi implementare un sottrattore binario a n bit, sovrapponendo 'n' sottrattori completi. Quindi, avremo due circuiti separati per l'addizione e la sottrazione binaria di due numeri binari.
Nel secondo metodo, possiamo usare lo stesso sommatore binario per sottrarre due numeri binari semplicemente apportando alcune modifiche nel secondo input. Quindi, viene eseguita un'operazione di addizione binaria interna, ma l'output è la sottrazione risultante.
Sappiamo che la sottrazione di due numeri binari A e B può essere scritta come,
$$ AB = A + \ sinistra (\: complimento \: di \: B \ destra di {2}) $$
$ \ Rightarrow AB = A + \ left ({1} \: compliment \: of \: B \ right) + 1 $
Sottrattore binario a 4 bit
Il sottrattore binario a 4 bit produce l'estensione subtraction of two 4-bit numbers. Siano i numeri binari a 4 bit, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ e $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Internamente, l'operazione del sottrattore binario a 4 bit è simile a quella del sommatore binario a 4 bit. Se i bit normali del numero binario A, i bit integrati del numero binario B e il riporto iniziale (prestito), C in come uno vengono applicati al sommatore binario a 4 bit, allora diventa sottrattore binario a 4 bit. Ilblock diagram di sottrattore binario a 4 bit è mostrato nella figura seguente.

Questo sottrattore binario a 4 bit produce un output, che ha al massimo 5 bit. Se il numero binario A è maggiore del numero binario B, allora MSB dell'uscita è zero e i bit rimanenti mantengono l'ampiezza di AB. Se il numero binario A è minore del numero binario B, allora MSB dell'output è uno. Quindi, prendi il complemento a 2 dell'output per ottenere la grandezza di AB.
In questo modo, possiamo implementare qualsiasi sottrattore binario di ordine superiore semplicemente mettendo in cascata il numero richiesto di sommatori completi con le modifiche necessarie.
Sommatore / sottrattore binario
Il circuito, che può essere utilizzato per eseguire l'addizione o la sottrazione di due numeri binari in qualsiasi momento, è noto come Binary Adder / subtractor. Sia il sommatore binario che il sottrattore binario contengono un set di sommatori completi, che sono a cascata. I bit di input del numero binario A vengono applicati direttamente sia nel sommatore binario che nel sottrattore binario.
Esistono due differenze negli input dei sommatori completi presenti in Binary adder e Binary subtractor.
I bit di input del numero binario B vengono applicati direttamente ai sommatori completi nel sommatore binario, mentre i bit complementati del numero binario B vengono applicati ai sommatori completi nel sottrattore binario.
Il riporto iniziale, C 0 = 0 viene applicato nel sommatore binario a 4 bit, mentre il riporto iniziale (prestito), C 0 = 1 viene applicato nel sottrattore binario a 4 bit.
Sappiamo che a 2-input Ex-OR gateproduce un output, che è uguale a quello del primo input quando l'altro input è zero. Allo stesso modo, produce un output, che è il complemento del primo input quando l'altro input è uno.
Pertanto, possiamo applicare i bit di ingresso del numero binario B, a porte Ex-OR a 2 ingressi. L'altro ingresso a tutte queste porte Ex-OR è C 0 . Quindi, in base al valore di C 0 , le porte Ex-OR producono i bit normali o completati del numero binario B.
Sommatore / sottrattore binario a 4 bit
Il sommatore / sottrattore binario a 4 bit produce l'addizione o la sottrazione di due numeri a 4 bit in base al valore di riporto o prestito iniziale, 0 . Siano i numeri binari a 4 bit, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ e $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Il funzionamento del sommatore / sottrattore binario a 4 bit è simile a quello del sommatore binario a 4 bit e del sottrattore binario a 4 bit.
Applicare i normali bit dei numeri binari A e B e portare o prendere in prestito iniziale, C 0 dall'esterno a un sommatore binario a 4 bit. Ilblock diagram di sommatore / sottrattore binario a 4 bit è mostrato nella figura seguente.
Se il riporto iniziale, 0 è zero, ogni sommatore completo ottiene i bit normali dei numeri binari A e B. Quindi, il sommatore / sottrattore binario a 4 bit produce un output, che è iladdition of two binary numbers A e B.
Se il prestito iniziale, 0 è uno, allora ogni sommatore completo ottiene i bit normali del numero binario A e i bit complementati del numero binario B. Quindi, il sommatore / sottrattore binario a 4 bit produce un output, che è ilsubtraction of two binary numbers A e B.
Pertanto, con l'aiuto di porte Ex-OR aggiuntive, lo stesso circuito può essere utilizzato sia per l'addizione che per la sottrazione di due numeri binari.