エミッタフォロワ&ダーリントンアンプ
エミッタフォロワとダーリントンアンプは、フィードバックアンプの最も一般的な例です。これらは、多くのアプリケーションで最もよく使用されるものです。
エミッタフォロワ
エミッタフォロワ回路は、フィードバックアンプにおいて重要な位置を占めています。エミッタフォロワは負電流フィードバック回路の場合です。これは主に信号発生器回路の最終段増幅器として使用されます。
エミッタフォロワの重要な機能は次のとおりです。
- 入力インピーダンスが高い
- 出力インピーダンスが低い
- インピーダンス整合に最適な回路です
これらすべての理想的な機能により、エミッタフォロワ回路の多くのアプリケーションが可能になります。電圧利得のない電流増幅回路です。
建設
エミッタフォロワ回路の構造の詳細は、通常のアンプとほぼ同じです。主な違いは、負荷R Lはコレクタ端子には存在しないが、回路のエミッタ端子には存在することです。したがって、出力はコレクタ端子ではなくエミッタ端子から取得されます。
バイアスは、ベース抵抗法または分圧器法のいずれかによって提供されます。次の図は、エミッタフォロワの回路図を示しています。

操作
入力信号電圧がベース-エミッタ間に印加され、出力電圧V開発O Rを横切るEエミッタ部にあります、。したがって、
$$ V_o = I_E R_E $$
この出力電流全体がフィードバックを介して入力に適用されます。したがって、
$$ V_f = V_o $$
R Lの両端に発生する出力電圧はエミッタ電流に比例するため、このエミッタフォロワ回路は電流フィードバック回路です。したがって、
$$ \ beta = \ frac {V_f} {V_o} = 1 $$
トランジスタ(= Vへの入力信号電圧こともが注目されているI Vの差に等しい)SとV Oすなわち、
$$ V_i = V_s-V_o $$
したがって、フィードバックは否定的です。
特徴
エミッタフォロワの主な特徴は次のとおりです。
- 電圧利得なし。実際、電圧ゲインはほぼ1です。
- 比較的高い電流ゲインと電力ゲイン。
- 高入力インピーダンスと低出力インピーダンス。
- 入力と出力のAC電圧は同相です。
エミッタフォロワの電圧利得
エミッタフォロワ回路が目立つので、エミッタフォロワ回路の電圧利得の式を取得してみましょう。エミッタフォロワ回路は次のようになります-
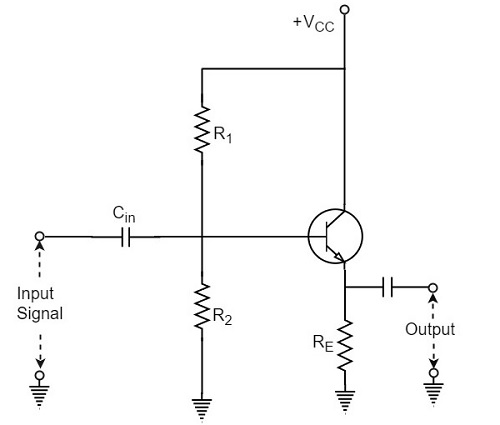
上記の回路のAC等価回路を描くと、エミッタバイパスコンデンサがないため、以下のようになります。

AC抵抗R Eエミッタ回路は次式で与えられます。
$$ r_E = r'_E + R_E $$
どこ
$$ r'_E = \ frac {25 mV} {I_E} $$
アンプの電圧利得を求めるために、上の図を次の図に置き換えることができます。
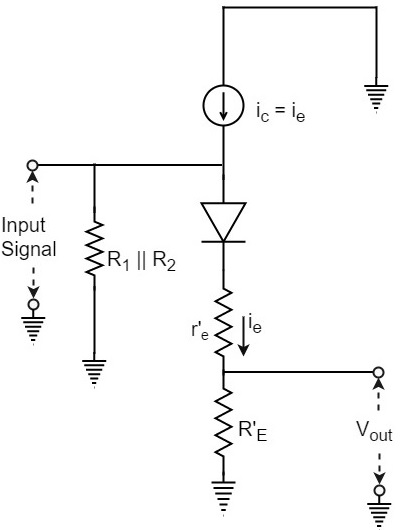
入力電圧がエミッタ回路、すなわち、(R」の交流抵抗の両端に印加されることに注意してくださいE + R E)。理想的であるとエミッタダイオードを仮定すると、出力電圧V outはなり
$$ V_ {out} = i_e R_E $$
入力電圧Vでになります
$$ V_ {in} = i_e(r'_e + R_E)$$
したがって、エミッタフォロワの電圧利得は次のようになります。
$$ A_V = \ frac {V_ {out}} {V_ {in}} = \ frac {i_e R_E} {i_e(r'_e + R_E)} = \ frac {R_E} {(r'_e + R_E)} $$
または
$$ A_V = \ frac {R_E} {(r'_e + R_E)} $$
ほとんどの実用的なアプリケーションでは、
$$ R_E \ gg r'_e $$
だから、A V ≈1.実際には、エミッタフォロワの電圧利得は0.8〜0.999の間です。
ダーリントンアンプ
今説明したエミッタフォロワ回路は、回路電流ゲイン(A i)と入力インピーダンス(Z i)の要件を満たすことができません。回路電流ゲインと入力インピーダンスの全体的な値をいくらか増加させるために、次の回路図に示すように2つのトランジスタを接続します。Darlington 構成。

上図に示すように、第1トランジスタのエミッタは第2トランジスタのベースに接続されています。両方のトランジスタのコレクタ端子は互いに接続されています。
バイアス分析
このタイプの接続のため、最初のトランジスタのエミッタ電流は2番目のトランジスタのベース電流にもなります。したがって、ペアの電流ゲインは、個々の電流ゲインの積に等しくなります。
$$ \ beta = \ beta _1 \ beta _2 $$
一般に、最小数のコンポーネントで高電流ゲインが達成されます。
ここでは2つのトランジスタが使用されているため、2つのVBEドロップを考慮する必要があります。バイアス分析は、他の点では1つのトランジスタで同様です。
R 2の両端の電圧、
$$ V_2 = \ frac {V_CC} {R_1 + R_2} \ times R_2 $$
R Eの両端の電圧、
$$ V_E = V_2-2 V_ {BE} $$
R Eを流れる電流、
$$ I_ {E2} = \ frac {V_2-2 V_ {BE}} {R_E} $$
トランジスタは直接結合されているので、
$$ I_ {E1} = I_ {B2} $$
今
$$ I_ {B2} = \ frac {I_ {E2}} {\ beta _2} $$
したがって、
$$ I_ {E1} = \ frac {I_ {E2}} {\ beta _2} $$
つまり、
$$ I_ {E1} = I_ {E1} \ beta _2 $$
我々は持っています
$ I_ {E1} = \ beta _1 I_ {B1} $($ I_ {E1} \ cong I_ {C1} $以降)
したがって、
$$ I_ {E2} = I_ {E1} \ beta _2 $$
我々は書ける
$$ I_ {E2} = \ beta _1 \ beta _2 I_ {B1} $$
したがって、電流ゲインは次のように与えることができます。
$$ \ beta = \ frac {I_ {E2}} {I_ {B1}} = \ frac {\ beta _1 \ beta _2 I_ {B1}} {I_ {B1}} = \ beta _1 \ beta_2 $$
ダーリントンアンプの入力インピーダンスは
{で} $ Z_ = \ beta_1 \ beta_2 R_E ..... $無視R」E
実際には、次の図に示すように、これら2つのトランジスタは1つのトランジスタハウジングに配置され、3つの端子はハウジングから取り出されます。

この3端子デバイスは次のように呼び出すことができます Darling ton transistor。ダーリントントランジスタは、高い電流ゲインと高い入力インピーダンスを備えた単一のトランジスタのように機能します。
特徴
ダーリントンアンプの重要な特徴は次のとおりです。
- 非常に高い入力インピーダンス(MΩ)。
- 非常に高い電流ゲイン(数千)。
- 非常に低い出力インピーダンス(数Ω)。
ダーリントンアンプの特性は基本的にエミッタフォロワの特性と同じであるため、2つの回路は同様のアプリケーションに使用されます。
これまで、正のフィードバックに基づくアンプについて説明してきました。トランジスタ回路の負帰還は、発振器の動作に役立ちます。オシレーターのトピックは、オシレーターのチュートリアルで完全にカバーされています。