トランジスタ負荷線解析
これまで、トランジスタのさまざまな動作領域について説明してきました。しかし、これらすべての領域の中で、トランジスタはアクティブ領域でうまく動作することがわかったため、次のようにも呼ばれます。linear region。トランジスタの出力は、コレクタ電流とコレクタ電圧です。
出力特性
トランジスタの出力特性を考慮すると、さまざまな入力値の曲線は次のようになります。

上の図では、出力特性はコレクタ電流の間に描かれています IC およびコレクター電圧 VCE ベース電流のさまざまな値に対して IB。ここでは、さまざまな出力曲線を取得するために、さまざまな入力値についてこれらを考慮します。
ロードライン
可能な最大コレクタ電流の値を考慮すると、そのポイントはY軸上に存在します。これは、 Saturation point。同様に、可能な最大コレクタエミッタ電圧の値を考慮すると、そのポイントはX軸上に存在します。Cutoff point。
これらの2点を結ぶ線を引くと、そのような線は次のように呼ばれます。 Load line。これは、負荷時の出力を表すために呼び出されます。この線は、出力特性曲線上に描かれると、と呼ばれる点で接触します。Operating point または quiescent point または単に Q-point。
ロードラインの概念は、次のグラフから理解できます。
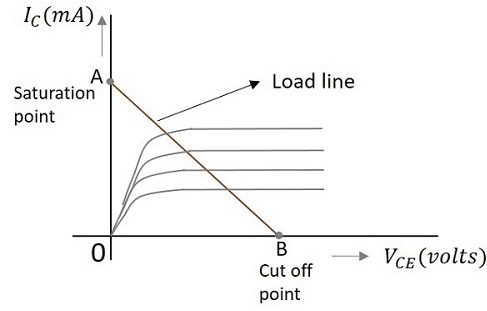
負荷線は、飽和点とカットオフ点を結合することによって描画されます。これら2つの間にある領域はlinear region。トランジスタは、この線形領域で優れた増幅器として機能します。
この負荷線がトランジスタにDCバイアスが与えられている場合にのみ描画される場合、 no input 信号が適用されると、そのような負荷線は次のように呼ばれます。 DC load line。一方、負荷線は、input signal DC電圧が印加されると、そのような線はと呼ばれます AC load line。
DC負荷線
トランジスタにバイアスが与えられ、その入力に信号が印加されていない場合、そのような条件下で引かれる負荷線は、次のように理解できます。 DC状態。ここでは増幅はありませんsignal is absent。回路は以下のようになります。

任意の時点でのコレクタエミッタ電圧の値は次のようになります。
$$ V_ {CE} = V_ {CC} -I_C R_C $$
VとしてCC及びR Cは固定値であり、上記のものは、第一次方程式であり、したがって、出力特性上の直線であろう。この行は次のように呼ばれますD.C. Load line。次の図は、DC負荷線を示しています。

負荷線を取得するには、直線の2つの端点を決定します。これらの2つの点をAとBとします。
Aを取得するには
電圧Vエミッタ場合コレクタCE = 0、コレクタ電流は最大値であり、Vに等しいCC / R C。これにより、VCEの最大値が得られます。これは次のように表示されます
$$ V_ {CE} = V_ {CC} -I_C R_C $$
$$ 0 = V_ {CC} -I_C R_C $$
$$ I_C = V_ {CC} / R_C $$
これにより、上の図に示すように、コレクタ電流軸上の点A(OA = V CC / R C)が得られます。
Bを取得するには
コレクタ電流IC = 0の場合、コレクタエミッタ電圧は最大になり、VCCに等しくなります。これが私の最大値与えCを。これは次のように表示されます
$$ V_ {CE} = V_ {CC} -I_C R_C $$
$$ = V_ {CC} $$
(AS I C = 0)
これにより、上図に示すコレクタエミッタ電圧軸上の(OB = V CC)を意味する点Bが得られます。
したがって、飽和点とカットオフ点の両方が決定され、負荷線が直線であることがわかりました。したがって、DC負荷線を引くことができます。
AC負荷線
前述のDC負荷線は、AC電圧が印加されていない場合のコレクター電流と電圧の変動を分析します。一方、AC負荷線は、ピークツーピーク電圧、または特定のアンプの可能な最大出力振幅を示します。
理解のために、CEアンプのAC等価回路を考えます。
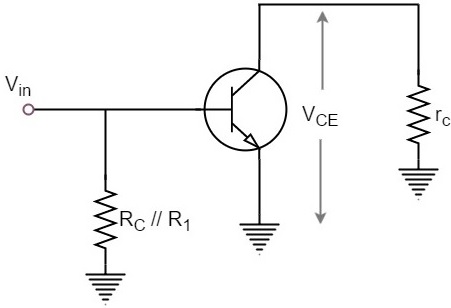
上図から、
$$ V_ {CE} =(R_C // R_1)\ times I_C $$
$$ r_C = R_C // R_1 $$
トランジスタが増幅器として動作するためには、トランジスタはアクティブ領域に留まっている必要があります。静止点は、最大入力信号の偏位が負と正の両方の半サイクルで対称になるように選択されます。
したがって、
$ V_ {max} = V_ {CEQ} $および$ V_ {min} = -V_ {CEQ} $
ここで、V CEQは、静止点でのエミッタ-コレクタ電圧です。
次のグラフは、飽和点とカットオフ点の間に引かれたAC負荷線を表しています。

上のグラフから、飽和点での電流ICは次のようになります。
$$ I_ {C(sat)} = I_ {CQ} +(V_ {CEQ} / r_C)$$
電圧V CEのカットオフ点では、
$$ V_ {CE(off)} = V_ {CEQ} + I_ {CQ} r_C $$
したがって、対応するV CEQ = V CEQ /(R C // R 1)の最大電流は次のようになります。
$$ I_ {CQ} = I_ {CQ} *(R_C // R_1)$$
したがって、静止電流を追加することにより、AC負荷線の終点は次のようになります。
$$ I_ {C(sat)} = I_ {CQ} + V_ {CEQ} /(R_C // R_1)$$
$$ V_ {CE(off)} = V_ {CEQ} + I_ {CQ} *(R_C // R_1)$$
ACおよびDC負荷線
AC負荷線とDC負荷線をグラフで表すと、同一ではないことがわかります。これらの線は両方ともで交差しますQ-point または quiescent point。AC負荷線の終点は、飽和点とカットオフポイントです。これは下の図からわかります。

上図から、ベース電流IBの値が10mAのときに静止点(濃い点)が得られていることがわかります。これは、AC負荷線とDC負荷線の両方が交差する点です。
次の章では、の概念について説明します。 quiescent point または operating point 詳細に。