記数法の変換
ご存知のように、10進数、2進数、8進数、16進数のシステムは位取り記数法です。2進数、8進数、16進数を10進数に変換するには、各桁の積とその位置の値を加算するだけです。ここでは、これらの数値システム間のその他の変換について学習します。
10進数から2進数
10進数は、余りを記録しながら2で除算を繰り返すことにより、2進数に変換できます。これがどのように発生するかを確認するために例を見てみましょう。
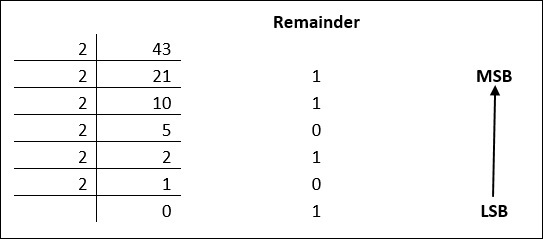
残りは下から上に読み取られ、同等のバイナリを取得します。
43 10 = 101011 2
10進数から8進数
余りを記録しながら、数値を8で除算することを繰り返すことにより、10進数を8進数に変換できます。これがどのように発生するかを確認するために例を見てみましょう。

残りを下から上に読んで、
473 10 = 731 8
10進数から16進数
10進数は、余りを記録しながら数値を16で除算することを繰り返すことにより、8進数に変換できます。これがどのように発生するかを確認するために例を見てみましょう。

残りを下から上に読むと、
423 10 = 1A7 16
2進数から8進数およびその逆
2進数を8進数に変換するには、次の手順に従います。
最下位ビットから始めて、3ビットのグループを作成します。
グループの作成に1ビットまたは2ビット少ない場合は、最上位ビットの後に0を追加できます。
各グループを同等の8進数に変換します
これを理解するために例を見てみましょう。
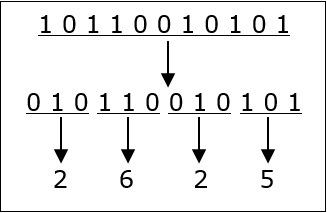
1011001010 12 = 2625 8
8進数を2進数に変換するには、この表に従って、各8進数を3ビットの2進数に変換します。
| 8進数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 同等のバイナリ | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
54673 8 = 101100110111011 2
バイナリから16進数
2進数を16進数に変換するには、次の手順に従います。
最下位ビットから始めて、4ビットのグループを作成します。
グループの作成に1ビットまたは2ビット少ない場合は、最上位ビットの後に0を追加できます。
各グループを同等の8進数に変換します。
これを理解するために例を見てみましょう。
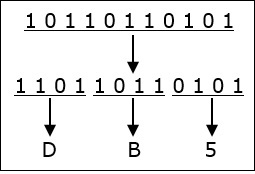
10110110101 2 = DB5 16
8進数を2進数に変換するには、各8進数を3ビットの2進数に変換します。