コンピュータの基礎-記数法
数字を表現して操作する手法は、 number system。 Decimal number system最も一般的な記数法です。他の人気のある番号システムには、 binary number system, octal number system, hexadecimal number system, 等
10進法
10進法は base 100から9までの10桁の記数法。これは、これらの10桁を使用して任意の数値を表すことができることを意味します。10進法もpositional value system。これは、数字の値がその位置に依存することを意味します。これを理解するために例を見てみましょう。
734、971、207の3つの数値があるとします。3つの数値すべての7の値は異なります-
- 734において、7の値は、7百または700、または7×100、または7×10 2
- 971において、7の値は7十または70または7×10、または7×10 1
- 207では、値0f7は7単位または7または7×1または7×100です。
各ポジションの重みは次のように表すことができます-

デジタルシステムでは、指示は電気信号を介して行われます。変化は、信号の電圧を変化させることによって行われます。デジタル機器に10進数システムを実装するために10の異なる電圧を持つことは困難です。そのため、デジタルで実装しやすい多くの番号システムが開発されています。それらを詳しく見ていきましょう。
2進数システム
電気信号を介して命令を変更する最も簡単な方法は、オンとオフの2状態システムです。オンは1として表され、オフは0として表されますが、0は実際には信号がないのではなく、より低い電圧の信号です。0と1の2桁だけの記数法は、binary number system。
各2進数は、 bit。2進数システムも位置値システムであり、ここに表示されているように、各桁の値は2の累乗で表されます。

任意の2進数では、右端の桁が呼び出されます least significant bit (LSB) 左端の数字は most significant bit (MSB)。
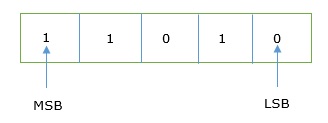
また、この数値に相当する10進数は、各桁とその位置の値の積の合計です。
11010 2 = 1×2 4 + 1×2 3 + 0×2 2 + 1×2 1 + 0×2 0
= 16 + 8 + 0 + 2 + 0
= 26 10
コンピュータのメモリは、格納できるビット数で測定されます。これは、メモリ容量変換のチャートです。
- 1バイト(B)= 8ビット
- 1キロバイト(KB)= 1024バイト
- 1メガバイト(MB)= 1024 KB
- 1ギガバイト(GB)= 1024 MB
- 1テラバイト(TB)= 1024 GB
- 1エクサバイト(EB)= 1024 PB
- 1ゼタバイト= 1024 EB
- 1ヨタバイト(YB)= 1024 ZB
8進数システム
Octal number system 0、1、2、3、4、5、6、7の8桁の数字があります。8進数システムも位置値システムであり、ここに示すように、各桁の値は8の累乗で表されます。

8進数に相当する10進数は、各桁とその位置の値の積の合計です。
726 8 = 7×8 2 + 2×8 1 + 6×8 0
= 448 + 16 + 6
= 470 10
16進数システム
Octal number system 16個の記号– 0から9およびAからF(Aは10に等しい)、Bは11に等しい、というようにFまで続きます。16進数システムも位置値システムであり、各桁の値は16の累乗で表されます。 、ここに示すように-

16進数に相当する10進数は、各桁とその位置の値の積の合計です。
27FB 16 = 2×16 3 + 7×16 2 + 15×16 1 + 10×16 0
= 8192 + 1792 + 240 +10
= 10234 10
記数法の関係
次の表は、10進数、2進数、8進数、16進数のシステム間の関係を示しています。
| 16進数 | 10進数 | オクタル | バイナリ |
|---|---|---|---|
| 0 | 0 | 0 | 0000 |
| 1 | 1 | 1 | 0001 |
| 2 | 2 | 2 | 0010 |
| 3 | 3 | 3 | 0011 |
| 4 | 4 | 4 | 0100 |
| 5 | 5 | 5 | 0101 |
| 6 | 6 | 6 | 0110 |
| 7 | 7 | 7 | 0111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| A | 10 | 12 | 1010 |
| B | 11 | 13 | 1011 |
| C | 12 | 14 | 1100 |
| D | 13 | 15 | 1101 |
| E | 14 | 16 | 1110 |
| F | 15 | 17 | 1111 |
ASCII
数値データに加えて、コンピューターは、英語の完全な文字セットを形成するアルファベット、句読点、数学演算子、特殊記号などを処理できる必要があります。文字または記号の完全なセットは、英数字コードと呼ばれます。完全な英数字コードには通常、次のものが含まれます。
- 26大文字
- 26の小文字
- 10桁
- 7つの句読点
- 20〜40個の特殊文字
これで、コンピューターは、使用されている記数法に関係なく、数値のみを理解します。したがって、すべての文字には、英数字コードと呼ばれる同等の数値が必要です。最も広く使用されている英数字コードは、情報交換のための米国標準コード(ASCII)です。ASCIIは、128(27)個の可能なコードを持つ7ビットコードです。

ISCII
ISCIIは Indian Script Code for Information Interchange。IISCIIは、コンピューター上でインドの言語をサポートするために開発されました。IISCIでサポートされている言語には、デーバナーガリー語、タミル語、ベンガル語、グジャラート語、グルムキ語、タミル語、テルグ語などがあります。IISCIは主に政府機関で使用されており、普及する前に、Unicode が導入されました。
Unicode
Unicodeは、さまざまな言語のスクリプトで使用するように設計された国際的なコーディングシステムです。各文字または記号には、主にASCIIのフレームワーク内で一意の数値が割り当てられます。以前は、各スクリプトには独自のエンコーディングシステムがあり、互いに競合する可能性がありました。
対照的に、これはUnicodeが公式に目指していることです。Unicodeは、プラットフォーム、プログラム、言語に関係なく、すべての文字に一意の番号を提供します。