データ構造-漸近解析

アルゴリズムの漸近分析とは、実行時のパフォーマンスの数学的境界/フレーミングを定義することです。漸近解析を使用すると、アルゴリズムの最良のケース、平均的なケース、および最悪のケースのシナリオを非常にうまく結論付けることができます。

漸近解析は入力バウンドです。つまり、アルゴリズムへの入力がない場合、一定時間で機能すると結論付けられます。「入力」を除いて、他のすべての要因は一定であると見なされます。

漸近分析とは、計算の数学的単位で任意の操作の実行時間を計算することを指します。たとえば、ある操作の実行時間はf（n）として計算され、別の操作の場合はg（n ²）として計算されます。これは、最初の操作の実行時間が増加に伴って直線的に増加することを意味しますn 2番目の操作の実行時間は、次の場合に指数関数的に増加します。 n増加します。同様に、両方の操作の実行時間は、次の場合にほぼ同じになります。n かなり小さいです。

通常、アルゴリズムに必要な時間は3つのタイプに分類されます-

Best Case −プログラムの実行に必要な最小時間。
Average Case −プログラムの実行に必要な平均時間。
Worst Case −プログラムの実行に必要な最大時間。

漸近表記

以下は、アルゴリズムの実行時間の複雑さを計算するために一般的に使用される漸近表記です。

Ο表記
Ω表記
θ表記

ランダウの記号、Ο

表記Ο（n）は、アルゴリズムの実行時間の上限を表す正式な方法です。これは、最悪の場合の時間計算量、またはアルゴリズムが完了するまでにかかる可能性のある最長時間を測定します。

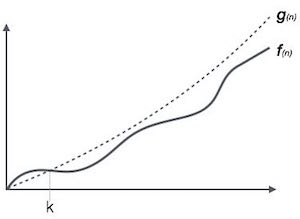
たとえば、関数の場合 f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

オメガ表記、Ω

表記Ω（n）は、アルゴリズムの実行時間の下限を表す正式な方法です。これは、最良の場合の時間計算量、またはアルゴリズムが完了するのにかかる可能性のある最良の時間を測定します。

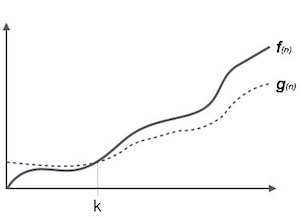
たとえば、関数の場合 f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

シータ表記、θ

表記θ（n）は、アルゴリズムの実行時間の下限と上限の両方を表す正式な方法です。それは次のように表されます-

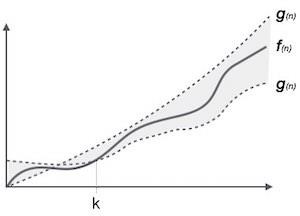
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

一般的な漸近表記

以下は、いくつかの一般的な漸近表記のリストです-

絶え間ない	−	Ο（1）
対数	−	Ο（log n）
線形	−	Ο（n）
n log n	−	Ο（n log n）
二次	−	Ο（n ²）
キュービック	−	Ο（n ³）
多項式	−	N ^Ο（1）
指数関数的	−	2 ^Ο（n）は