データ構造とアルゴリズム-クイックガイド
データ構造は、データを効率的に使用するためにデータを整理する体系的な方法です。以下の用語は、データ構造の基本用語です。
Interface−各データ構造にはインターフェースがあります。インターフェイスは、データ構造がサポートする一連の操作を表します。インターフェイスは、サポートされている操作のリスト、受け入れることができるパラメーターのタイプ、およびこれらの操作のタイプを返すだけです。
Implementation−実装は、データ構造の内部表現を提供します。実装は、データ構造の操作で使用されるアルゴリズムの定義も提供します。
データ構造の特徴
Correctness −データ構造の実装では、そのインターフェイスを正しく実装する必要があります。
Time Complexity −データ構造の実行時間または操作の実行時間は可能な限り短くする必要があります。
Space Complexity −データ構造演算のメモリ使用量はできるだけ少なくする必要があります。
データ構造の必要性
アプリケーションが複雑になり、データが豊富になるにつれて、アプリケーションが現在直面している3つの一般的な問題があります。
Data Search−店舗の100万(10 6)アイテムの在庫を考えます。アプリケーションがアイテムを検索する場合、検索が遅くなるたびに100万(10 6)アイテムのアイテムを検索する必要があります。データが大きくなると、検索が遅くなります。
Processor speed −プロセッサの速度は非常に高速ですが、データが10億レコードに増えると制限されます。
Multiple requests −数千人のユーザーがWebサーバー上で同時にデータを検索できるため、高速サーバーでさえデータの検索中に失敗します。
上記の問題を解決するために、データ構造が救いの手を差し伸べます。すべての項目を検索する必要がないようにデータをデータ構造に編成でき、必要なデータをほぼ瞬時に検索できます。
実行時間のケース
通常、さまざまなデータ構造の実行時間を相対的な方法で比較するために使用される3つのケースがあります。
Worst Case−これは、特定のデータ構造操作にかかる最大の時間がかかるシナリオです。操作の最悪の場合の時間がƒ(n)である場合、この操作はƒ(n)時間より長くはかかりません。ここで、ƒ(n)はnの関数を表します。
Average Case−これは、データ構造の操作の平均実行時間を表すシナリオです。操作の実行にƒ(n)時間がかかる場合、m回の操作にはmƒ(n)時間がかかります。
Best Case−これは、データ構造の操作の実行時間を可能な限り最小にするシナリオです。操作の実行にƒ(n)時間がかかる場合、実際の操作は、ƒ(n)として最大になる乱数として時間がかかる場合があります。
基本的な用語
Data −データは値または値のセットです。
Data Item −データ項目は単一の値の単位を参照します。
Group Items −サブアイテムに分割されたデータアイテムは、グループアイテムと呼ばれます。
Elementary Items −分割できないデータ項目を基本項目と呼びます。
Attribute and Entity −エンティティとは、値が割り当てられる可能性のある特定の属性またはプロパティを含むエンティティです。
Entity Set −同様の属性のエンティティがエンティティセットを形成します。
Field −フィールドは、エンティティの属性を表す単一の基本的な情報単位です。
Record −レコードは、特定のエンティティのフィールド値のコレクションです。
File −ファイルは、特定のエンティティセット内のエンティティのレコードのコレクションです。
オプションオンラインでお試しください
Cプログラミング言語の学習を開始するために、独自の環境を設定する必要はありません。理由は非常に単純です。すでにオンラインでCプログラミング環境をセットアップしているため、理論作業を行うときに、利用可能なすべての例をオンラインで同時にコンパイルして実行できます。これにより、読んでいる内容に自信が持てるようになり、さまざまなオプションで結果を確認できます。例を自由に変更して、オンラインで実行してください。
次の例を使用してみてください Try it サンプルコードボックスの右上隅にあるオプション-
#include <stdio.h>
int main(){
/* My first program in C */
printf("Hello, World! \n");
return 0;
}このチュートリアルに記載されているほとんどの例には、[試してみる]オプションがありますので、それを利用して学習を楽しんでください。
ローカル環境のセットアップ
それでもCプログラミング言語用の環境をセットアップする場合は、コンピューターで使用できる次の2つのツール((a)テキストエディターと(b)Cコンパイラー)が必要です。
テキストエディタ
これは、プログラムの入力に使用されます。いくつかのエディターの例には、Windowsメモ帳、OS Editコマンド、Brief、Epsilon、EMACS、vimまたはviが含まれます。
テキストエディタの名前とバージョンは、オペレーティングシステムによって異なる場合があります。たとえば、メモ帳はWindowsで使用され、vimまたはviはWindowsだけでなく、LinuxまたはUNIXでも使用できます。
エディタで作成するファイルはソースファイルと呼ばれ、プログラムのソースコードが含まれています。Cプログラムのソースファイルには、通常、拡張子「」が付いています。.c"。
プログラミングを開始する前に、テキストエディタが1つあり、コンピュータプログラムを作成し、ファイルに保存し、コンパイルして、最後に実行するのに十分な経験があることを確認してください。
Cコンパイラ
ソースファイルに記述されているソースコードは、プログラムの人間が読める形式のソースです。CPUが指定された指示に従って実際にプログラムを実行できるように、機械語に変換するには「コンパイル」する必要があります。
このCプログラミング言語コンパイラは、ソースコードを最終的な実行可能プログラムにコンパイルするために使用されます。プログラミング言語コンパイラに関する基本的な知識があることを前提としています。
最も頻繁に使用され、無料で利用できるコンパイラは、GNU C / C ++コンパイラです。それ以外の場合は、それぞれのオペレーティングシステム(OS)がある場合は、HPまたはSolarisのいずれかのコンパイラを使用できます。
次のセクションでは、さまざまなOSにGNU C / C ++コンパイラをインストールする方法について説明します。GNUGCCコンパイラはCとC ++の両方のプログラミング言語で機能するため、C / C ++について一緒に言及しています。
UNIX / Linuxへのインストール
使用している場合 Linux or UNIX、次に、コマンドラインから次のコマンドを入力して、GCCがシステムにインストールされているかどうかを確認します-
$ gcc -vマシンにGNUコンパイラがインストールされている場合は、次のようなメッセージが出力されます。
Using built-in specs.
Target: i386-redhat-linux
Configured with: ../configure --prefix = /usr .......
Thread model: posix
gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)GCCがインストールされていない場合は、で入手可能な詳細な手順を使用して自分でインストールする必要があります。 https://gcc.gnu.org/install/
このチュートリアルはLinuxに基づいて作成されており、記載されているすべての例はLinuxシステムのCentOSフレーバーでコンパイルされています。
MacOSへのインストール
Mac OS Xを使用している場合、GCCを入手する最も簡単な方法は、AppleのWebサイトからXcode開発環境をダウンロードし、簡単なインストール手順に従うことです。Xcodeをセットアップすると、C / C ++用のGNUコンパイラを使用できるようになります。
Xcodeは現在developer.apple.com/technologies/tools/で入手できます。
Windowsへのインストール
WindowsにGCCをインストールするには、MinGWをインストールする必要があります。MinGWをインストールするには、MinGWホームページwww.mingw.orgにアクセスし、MinGWダウンロードページへのリンクをたどります。MinGW- <version> .exeという名前のMinGWインストールプログラムの最新バージョンをダウンロードします。
MinWGのインストール中に、少なくともgcc-core、gcc-g ++、binutils、およびMinGWランタイムをインストールする必要がありますが、さらにインストールすることもできます。
MinGWインストールのbinサブディレクトリをに追加します PATH 環境変数。これらのツールをコマンドラインで単純な名前で指定できます。
インストールが完了すると、Windowsコマンドラインからgcc、g ++、ar、ranlib、dlltool、およびその他のいくつかのGNUツールを実行できるようになります。
アルゴリズムは段階的な手順であり、目的の出力を取得するために特定の順序で実行される一連の命令を定義します。アルゴリズムは通常、基礎となる言語から独立して作成されます。つまり、アルゴリズムは複数のプログラミング言語で実装できます。
データ構造の観点から、以下はアルゴリズムのいくつかの重要なカテゴリです-
Search −データ構造内のアイテムを検索するアルゴリズム。
Sort −アイテムを特定の順序で並べ替えるアルゴリズム。
Insert −データ構造にアイテムを挿入するアルゴリズム。
Update −データ構造内の既存のアイテムを更新するアルゴリズム。
Delete −データ構造から既存のアイテムを削除するアルゴリズム。
アルゴリズムの特徴
すべてのプロシージャをアルゴリズムと呼ぶことができるわけではありません。アルゴリズムには次の特性が必要です-
Unambiguous−アルゴリズムは明確で明確でなければなりません。その各ステップ(またはフェーズ)、およびそれらの入力/出力は明確である必要があり、1つの意味のみにつながる必要があります。
Input −アルゴリズムには、0個以上の明確に定義された入力が必要です。
Output −アルゴリズムには、明確に定義された1つ以上の出力があり、目的の出力と一致している必要があります。
Finiteness −アルゴリズムは、有限のステップ数の後に終了する必要があります。
Feasibility −利用可能なリソースで実行可能である必要があります。
Independent −アルゴリズムには段階的な指示が必要であり、プログラミングコードから独立している必要があります。
アルゴリズムの書き方は?
アルゴリズムを作成するための明確に定義された標準はありません。むしろ、それは問題とリソースに依存します。特定のプログラミングコードをサポートするようにアルゴリズムが作成されることはありません。
すべてのプログラミング言語は、ループ(do、for、while)、フロー制御(if-else)などの基本的なコード構造を共有していることがわかっています。これらの一般的な構造を使用して、アルゴリズムを記述できます。
アルゴリズムは段階的に記述しますが、常にそうであるとは限りません。アルゴリズムの記述はプロセスであり、問題のドメインが明確に定義された後に実行されます。つまり、ソリューションを設計している問題のドメインを知る必要があります。
例
例を使ってアルゴリズムの書き方を学んでみましょう。
Problem − 2つの数値を加算し、結果を表示するアルゴリズムを設計します。
Step 1 − START
Step 2 − declare three integers a, b & c
Step 3 − define values of a & b
Step 4 − add values of a & b
Step 5 − store output of step 4 to c
Step 6 − print c
Step 7 − STOPアルゴリズムは、プログラマーにプログラムのコーディング方法を指示します。あるいは、アルゴリズムは次のように書くことができます-
Step 1 − START ADD
Step 2 − get values of a & b
Step 3 − c ← a + b
Step 4 − display c
Step 5 − STOPアルゴリズムの設計と分析では、通常、2番目の方法を使用してアルゴリズムを記述します。これにより、アナリストは不要な定義をすべて無視してアルゴリズムを簡単に分析できます。彼は、使用されている操作とプロセスの流れを観察できます。
書き込み step numbers、はオプションです。
与えられた問題の解決策を得るためのアルゴリズムを設計します。問題は複数の方法で解決できます。
したがって、特定の問題に対して多くのソリューションアルゴリズムを導出できます。次のステップは、提案されたソリューションアルゴリズムを分析し、最適なソリューションを実装することです。
アルゴリズム分析
アルゴリズムの効率は、実装前と実装後の2つの異なる段階で分析できます。それらは次のとおりです-
A Priori Analysis−これはアルゴリズムの理論的分析です。アルゴリズムの効率は、プロセッサ速度などの他のすべての要因が一定であり、実装に影響を与えないと仮定して測定されます。
A Posterior Analysis−これはアルゴリズムの経験的分析です。選択したアルゴリズムは、プログラミング言語を使用して実装されます。次に、これはターゲットコンピュータマシンで実行されます。この分析では、実行時間や必要なスペースなどの実際の統計が収集されます。
先験的なアルゴリズム分析について学びます。アルゴリズム分析は、関連するさまざまな操作の実行時間または実行時間を扱います。操作の実行時間は、操作ごとに実行されるコンピューター命令の数として定義できます。
アルゴリズムの複雑さ
仮定します X はアルゴリズムであり、 n は入力データのサイズであり、アルゴリズムXによって使用される時間と空間は、Xの効率を決定する2つの主な要因です。
Time Factor −時間は、ソートアルゴリズムでの比較などの主要な操作の数をカウントすることによって測定されます。
Space Factor −スペースは、アルゴリズムに必要な最大メモリスペースをカウントすることによって測定されます。
アルゴリズムの複雑さ f(n) 実行時間および/またはアルゴリズムに必要なストレージスペースを n 入力データのサイズとして。
スペースの複雑さ
アルゴリズムのスペースの複雑さは、アルゴリズムのライフサイクルで必要なメモリスペースの量を表します。アルゴリズムに必要なスペースは、次の2つのコンポーネントの合計に等しくなります-
問題のサイズに依存しない、特定のデータと変数を格納するために必要なスペースである固定部分。たとえば、使用される単純な変数と定数、プログラムサイズなど。
変数部分は変数に必要なスペースであり、そのサイズは問題のサイズによって異なります。たとえば、動的メモリ割り当て、再帰スタックスペースなど。
任意のアルゴリズムPの空間複雑度S(P)はS(P)= C + SP(I)です。ここで、Cは固定部分であり、S(I)はアルゴリズムの可変部分であり、インスタンスの特性Iに依存します。概念を説明しようとする簡単な例です-
Algorithm: SUM(A, B)
Step 1 - START
Step 2 - C ← A + B + 10
Step 3 - Stopここでは、3つの変数A、B、Cと1つの定数があります。したがって、S(P)= 1 + 3です。ここで、スペースは指定された変数と定数タイプのデータ型に依存し、それに応じて乗算されます。
時間計算量
アルゴリズムの時間計算量は、アルゴリズムが実行して完了するまでに必要な時間を表します。時間要件は、数値関数T(n)として定義できます。ここで、T(n)は、各ステップが一定の時間を消費する場合、ステップ数として測定できます。
たとえば、2つのnビット整数を加算するには nステップ。したがって、合計計算時間はT(n)= c ∗ nです。ここで、cは2ビットの加算にかかる時間です。ここでは、入力サイズが大きくなるにつれてT(n)が直線的に大きくなることがわかります。
アルゴリズムの漸近分析とは、実行時のパフォーマンスの数学的境界/フレーミングを定義することです。漸近解析を使用すると、アルゴリズムの最良のケース、平均的なケース、および最悪のケースのシナリオを非常にうまく結論付けることができます。
漸近解析は入力バウンドです。つまり、アルゴリズムへの入力がない場合、一定時間で機能すると結論付けられます。「入力」を除いて、他のすべての要因は一定であると見なされます。
漸近分析とは、計算の数学的単位で任意の操作の実行時間を計算することを指します。たとえば、ある操作の実行時間はf(n)として計算され、別の操作の場合はg(n 2)として計算されます。これは、最初の操作の実行時間が増加に伴って直線的に増加することを意味します。n 2番目の操作の実行時間は、次の場合に指数関数的に増加します。 n増加します。同様に、両方の操作の実行時間は、次の場合にほぼ同じになります。n かなり小さいです。
通常、アルゴリズムに必要な時間は3つのタイプに分類されます-
Best Case −プログラムの実行に必要な最小時間。
Average Case −プログラムの実行に必要な平均時間。
Worst Case −プログラムの実行に必要な最大時間。
漸近表記
以下は、アルゴリズムの実行時間の複雑さを計算するために一般的に使用される漸近表記です。
- Ο表記
- Ω表記
- θ表記
ランダウの記号、Ο
表記Ο(n)は、アルゴリズムの実行時間の上限を表す正式な方法です。これは、最悪の場合の時間計算量、またはアルゴリズムが完了するまでにかかる可能性のある最長時間を測定します。
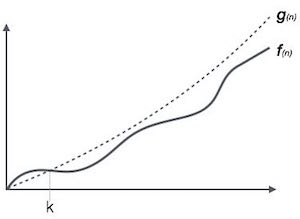
たとえば、関数の場合 f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }オメガ表記、Ω
表記Ω(n)は、アルゴリズムの実行時間の下限を表す正式な方法です。これは、最良の場合の時間計算量、またはアルゴリズムが完了するのにかかる可能性のある最良の時間を測定します。
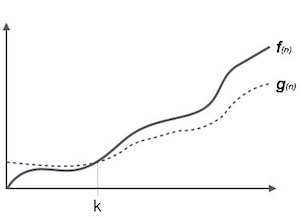
たとえば、関数の場合 f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }シータ表記、θ
表記θ(n)は、アルゴリズムの実行時間の下限と上限の両方を表す正式な方法です。それは次のように表されます-
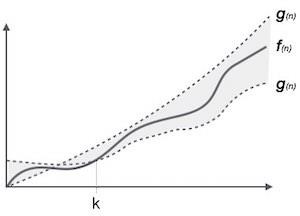
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }一般的な漸近表記
以下は、いくつかの一般的な漸近表記のリストです-
| 絶え間ない | − | Ο(1) |
| 対数 | − | Ο(log n) |
| 線形 | − | Ο(n) |
| n log n | − | Ο(n log n) |
| 二次 | − | Ο(n 2) |
| キュービック | − | Ο(n 3) |
| 多項式 | − | N Ο(1) |
| 指数関数的 | − | 2 Ο(n)は |
アルゴリズムは、特定の問題に対して最適なソリューションを実現するように設計されています。欲張りアルゴリズムのアプローチでは、決定は特定のソリューションドメインから行われます。貪欲であるため、最適なソリューションを提供すると思われる最も近いソリューションが選択されます。
欲張りアルゴリズムは、ローカライズされた最適なソリューションを見つけようとします。これにより、最終的にはグローバルに最適化されたソリューションにつながる可能性があります。ただし、一般的に欲張りアルゴリズムは、グローバルに最適化されたソリューションを提供しません。
コインを数える
この問題は、可能な限り最小のコインを選択することによって目的の値にカウントすることであり、貪欲なアプローチにより、アルゴリズムは可能な限り最大のコインを選択するように強制されます。1、2、5、10ポンドのコインが提供され、18ポンドを数えるように求められた場合、貪欲な手順は次のようになります。
1 −£10コインを1つ選択すると、残りのカウントは8になります
2 −次に、5ポンド硬貨を1枚選択すると、残りの数は3になります。
3 −次に、2ポンド硬貨を1枚選択すると、残りの数は1になります。
4 −そして最後に、1枚の1ポンド硬貨を選択することで問題が解決します
うまく機能しているようですが、このカウントでは4枚のコインを選ぶだけで済みます。しかし、問題を少し変えると、同じアプローチでは同じ最適な結果が得られない可能性があります。
1、7、10の値のコインがある通貨システムの場合、値18のコインを数えるのが絶対に最適ですが、15のような数の場合、必要以上のコインを使用する可能性があります。たとえば、欲張りアプローチでは、10 + 1 + 1 + 1 + 1 + 1、合計6コインを使用します。同じ問題は3枚のコイン(7 + 7 + 1)だけを使用することで解決できましたが
したがって、貪欲なアプローチは即座に最適化されたソリューションを選択し、グローバルな最適化が主要な懸念事項である場合は失敗する可能性があると結論付けることができます。
例
ほとんどのネットワークアルゴリズムは欲張りアプローチを使用します。ここにそれらのいくつかのリストがあります-
- 巡回セールスマン問題
- プリムの最小スパニングツリーアルゴリズム
- クラスカルの最小スパニングツリーアルゴリズム
- ダイクストラの最小スパニングツリーアルゴリズム
- グラフ-マップのカラーリング
- グラフ-頂点被覆
- ナップサック問題
- ジョブスケジューリング問題
貪欲なアプローチを使用して最適な解決策を見つける同様の問題がたくさんあります。
分割統治法では、手元にある問題をより小さなサブ問題に分割し、各問題を個別に解決します。サブ問題をさらに小さなサブ問題に分割し続けると、最終的にはそれ以上分割できない段階に達する可能性があります。それらの「原子的」で可能な最小のサブ問題(分数)が解決されます。元の問題の解決策を得るために、すべてのサブ問題の解決策が最終的にマージされます。
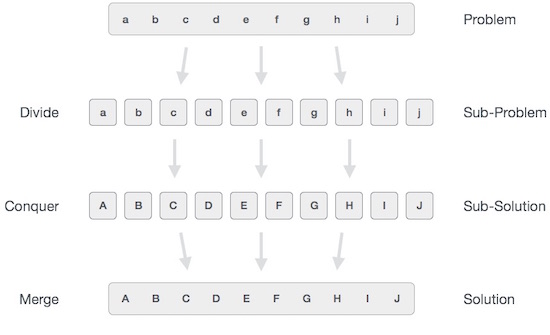
大まかに理解できます divide-and-conquer 3段階のプロセスでアプローチします。
分割/分割
このステップでは、問題をより小さなサブ問題に分割します。サブ問題は、元の問題の一部を表す必要があります。このステップでは、通常、再帰的なアプローチを使用して、サブ問題がさらに分割できなくなるまで問題を分割します。この段階で、サブ問題は本質的にアトミックになりますが、それでも実際の問題の一部を表しています。
征服/解決
このステップには、解決すべき小さなサブ問題がたくさんあります。一般に、このレベルでは、問題はそれ自体で「解決済み」と見なされます。
マージ/結合
小さなサブ問題が解決されると、この段階では、元の問題の解決策が定式化されるまで、それらを再帰的に結合します。このアルゴリズムによるアプローチは再帰的に機能し、征服とマージのステップは非常に近く機能するため、1つに見えます。
例
次のコンピュータアルゴリズムはに基づいています divide-and-conquer プログラミングアプローチ-
- マージソート
- クイックソート
- 二分探索
- Strassenの行列乗算
- 最も近いペア(ポイント)
コンピュータの問題を解決するために利用できるさまざまな方法がありますが、上記は分割統治法の良い例です。
動的計画法のアプローチは、分割統治法に似ており、問題をより小さな、さらにはより小さな可能なサブ問題に分解します。しかし、分割統治法とは異なり、これらのサブ問題は独立して解決されません。むしろ、これらの小さなサブ問題の結果が記憶され、類似または重複するサブ問題に使用されます。
動的計画法は、問題が発生した場合に使用されます。問題は、同様のサブ問題に分割できるため、結果を再利用できます。ほとんどの場合、これらのアルゴリズムは最適化に使用されます。手元のサブ問題を解決する前に、動的アルゴリズムは以前に解決されたサブ問題の結果を調べようとします。最良の解決策を達成するために、サブ問題の解決策が組み合わされます。
だから私たちはそれを言うことができます-
問題は、より小さな重複するサブ問題に分割できるはずです。
最適なソリューションは、より小さなサブ問題の最適なソリューションを使用することで実現できます。
動的アルゴリズムはメモ化を使用します。
比較
ローカル最適化に対処する欲張りアルゴリズムとは対照的に、動的アルゴリズムは問題の全体的な最適化に動機付けられます。
分割統治アルゴリズムでは、ソリューションを組み合わせて全体的なソリューションを実現するのとは対照的に、動的アルゴリズムは、小さなサブ問題の出力を使用してから、大きなサブ問題を最適化しようとします。動的アルゴリズムは、メモ化を使用して、すでに解決されたサブ問題の出力を記憶します。
例
以下のコンピューターの問題は、動的計画法を使用して解決できます。
- フィボナッチ数列
- ナップサック問題
- ハノイの塔
- Floyd-Warshallによるすべてのペアの最短経路
- ダイクストラによる最短経路
- プロジェクトのスケジューリング
動的計画法は、トップダウンとボトムアップの両方の方法で使用できます。そしてもちろん、ほとんどの場合、前のソリューション出力を参照する方が、CPUサイクルの観点から再計算するよりも安価です。
この章では、データ構造に関連する基本的な用語について説明します。
データ定義
データ定義は、次の特性を持つ特定のデータを定義します。
Atomic −定義は単一の概念を定義する必要があります。
Traceable −定義はいくつかのデータ要素にマッピングできる必要があります。
Accurate −定義は明確でなければなりません。
Clear and Concise −定義は理解できるものでなければなりません。
データオブジェクト
データオブジェクトは、データを持つオブジェクトを表します。
データ・タイプ
データ型は、整数、文字列などのさまざまな種類のデータを分類する方法であり、対応する種類のデータで使用できる値、対応する種類のデータで実行できる操作の種類を決定します。2つのデータ型があります-
- 組み込みデータ型
- 派生データ型
組み込みデータ型
言語に組み込みのサポートがあるデータ型は、組み込みデータ型と呼ばれます。たとえば、ほとんどの言語は次の組み込みデータ型を提供します。
- Integers
- ブール(true、false)
- 浮動小数点(10進数)
- 文字と文字列
派生データ型
いずれかの方法で実装できるため、実装に依存しないデータ型は、派生データ型と呼ばれます。これらのデータ型は通常、プライマリデータ型または組み込みデータ型とそれらに対する関連操作の組み合わせによって構築されます。例-
- List
- Array
- Stack
- Queue
基本操作
データ構造内のデータは、特定の操作によって処理されます。選択される特定のデータ構造は、データ構造に対して実行する必要のある操作の頻度に大きく依存します。
- Traversing
- Searching
- Insertion
- Deletion
- Sorting
- Merging
配列は、固定数のアイテムを保持できるコンテナであり、これらのアイテムは同じタイプである必要があります。ほとんどのデータ構造は、配列を使用してアルゴリズムを実装します。以下は、配列の概念を理解するための重要な用語です。
Element −配列に格納されている各アイテムは要素と呼ばれます。
Index −配列内の要素の各位置には、要素を識別するために使用される数値インデックスがあります。
配列表現
配列は、さまざまな言語でさまざまな方法で宣言できます。説明のために、C配列宣言を見てみましょう。

配列は、さまざまな言語でさまざまな方法で宣言できます。説明のために、C配列宣言を見てみましょう。
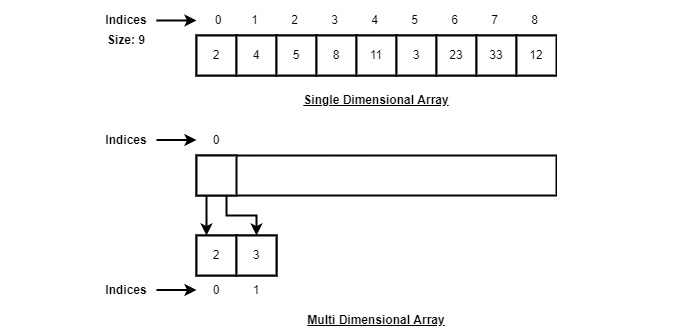
上の図のように、以下は考慮すべき重要なポイントです。
インデックスは0から始まります。
配列の長さは10です。これは、10個の要素を格納できることを意味します。
各要素には、そのインデックスを介してアクセスできます。たとえば、インデックス6の要素を9としてフェッチできます。
基本操作
アレイでサポートされる基本的な操作は次のとおりです。
Traverse −すべての配列要素を1つずつ出力します。
Insertion −指定されたインデックスに要素を追加します。
Deletion −指定されたインデックスの要素を削除します。
Search −指定されたインデックスまたは値を使用して要素を検索します。
Update −指定されたインデックスの要素を更新します。
Cでは、配列がサイズで初期化されると、次の順序で要素にデフォルト値が割り当てられます。
| データ・タイプ | デフォルト値 |
|---|---|
| ブール | false |
| char | 0 |
| int | 0 |
| 浮く | 0.0 |
| ダブル | 0.0f |
| ボイド | |
| wchar_t | 0 |
トラバース操作
この操作は、配列の要素をトラバースすることです。
例
次のプログラムは、配列の要素をトラバースして出力します。
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}上記のプログラムをコンパイルして実行すると、次の結果が得られます。
出力
The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8挿入操作
挿入操作は、1つ以上のデータ要素を配列に挿入することです。要件に基づいて、配列の最初、最後、または任意のインデックスに新しい要素を追加できます。
ここでは、配列の最後にデータを追加する挿入操作の実際的な実装を示しています。
例
以下は、上記のアルゴリズムの実装です-
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
n = n + 1;
while( j >= k) {
LA[j+1] = LA[j];
j = j - 1;
}
LA[k] = item;
printf("The array elements after insertion :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}上記のプログラムをコンパイルして実行すると、次の結果が得られます。
出力
The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
The array elements after insertion :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 10
LA[4] = 7
LA[5] = 8配列挿入操作の他のバリエーションについては、ここをクリックしてください
削除操作
削除とは、既存の要素を配列から削除し、配列のすべての要素を再編成することです。
アルゴリズム
検討する LA は線形配列です N 要素と K は次のような正の整数です K<=N。以下は、LAのK番目の位置で使用可能な要素を削除するアルゴリズムです。
1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop例
以下は、上記のアルゴリズムの実装です-
#include <stdio.h>
void main() {
int LA[] = {1,3,5,7,8};
int k = 3, n = 5;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
j = k;
while( j < n) {
LA[j-1] = LA[j];
j = j + 1;
}
n = n -1;
printf("The array elements after deletion :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}上記のプログラムをコンパイルして実行すると、次の結果が得られます。
出力
The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
The array elements after deletion :
LA[0] = 1
LA[1] = 3
LA[2] = 7
LA[3] = 8検索操作
値またはインデックスに基づいて配列要素の検索を実行できます。
アルゴリズム
検討する LA は線形配列です N 要素と K は次のような正の整数です K<=N。以下は、順次検索を使用してITEMの値を持つ要素を見つけるアルゴリズムです。
1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop例
以下は、上記のアルゴリズムの実装です-
#include <stdio.h>
void main() {
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0, j = 0;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
while( j < n){
if( LA[j] == item ) {
break;
}
j = j + 1;
}
printf("Found element %d at position %d\n", item, j+1);
}上記のプログラムをコンパイルして実行すると、次の結果が得られます。
出力
The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
Found element 5 at position 3更新操作
更新操作とは、指定されたインデックスの配列から既存の要素を更新することです。
アルゴリズム
検討する LA は線形配列です N 要素と K は次のような正の整数です K<=N。以下は、LAのK番目の位置で使用可能な要素を更新するためのアルゴリズムです。
1. Start
2. Set LA[K-1] = ITEM
3. Stop例
以下は、上記のアルゴリズムの実装です-
#include <stdio.h>
void main() {
int LA[] = {1,3,5,7,8};
int k = 3, n = 5, item = 10;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
LA[k-1] = item;
printf("The array elements after updation :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}上記のプログラムをコンパイルして実行すると、次の結果が得られます。
出力
The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
The array elements after updation :
LA[0] = 1
LA[1] = 3
LA[2] = 10
LA[3] = 7
LA[4] = 8リンクリストは、リンクを介して相互に接続された一連のデータ構造です。
リンクリストは、アイテムを含む一連のリンクです。各リンクには、別のリンクへの接続が含まれています。リンクリストは、配列に次いで2番目に使用されるデータ構造です。以下は、リンクリストの概念を理解するための重要な用語です。
Link −リンクリストの各リンクには、要素と呼ばれるデータを格納できます。
Next −リンクリストの各リンクには、Nextと呼ばれる次のリンクへのリンクが含まれています。
LinkedList −リンクリストには、Firstと呼ばれる最初のリンクへの接続リンクが含まれています。
リンクリスト表現
リンクリストは、すべてのノードが次のノードを指すノードのチェーンとして視覚化できます。

上の図のように、以下は考慮すべき重要なポイントです。
リンクリストには、firstというリンク要素が含まれています。
各リンクには、データフィールドとnextと呼ばれるリンクフィールドがあります。
各リンクは、次のリンクを使用して次のリンクにリンクされます。
最後のリンクは、リストの終わりを示すためにnullとしてリンクを運びます。
リンクリストの種類
以下は、さまざまなタイプのリンクリストです。
Simple Linked List −アイテムのナビゲーションは前方のみです。
Doubly Linked List −アイテムは前後に移動できます。
Circular Linked List −最後の項目には、次のように最初の要素のリンクが含まれ、最初の要素には前のように最後の要素へのリンクがあります。
基本操作
以下は、リストでサポートされている基本的な操作です。
Insertion −リストの先頭に要素を追加します。
Deletion −リストの先頭にある要素を削除します。
Display −完全なリストを表示します。
Search −指定されたキーを使用して要素を検索します。
Delete −指定されたキーを使用して要素を削除します。
挿入操作
リンクリストに新しいノードを追加することは、複数のステップのアクティビティです。ここで図を使ってこれを学びます。まず、同じ構造を使用してノードを作成し、それを挿入する必要がある場所を見つけます。

ノードを挿入していると想像してください B (NewNode)、間 A (LeftNode)と C(RightNode)。次に、Cの横にあるBをポイントします。
NewNode.next −> RightNode;このようになります-

これで、左側の次のノードが新しいノードを指すようになります。
LeftNode.next −> NewNode;
これにより、新しいノードが2つの中間に配置されます。新しいリストは次のようになります-

ノードがリストの先頭に挿入されている場合も、同様の手順を実行する必要があります。最後に挿入している間、リストの最後から2番目のノードは新しいノードを指し、新しいノードはNULLを指します。
削除操作
削除も複数のステップのプロセスです。絵で学びましょう。まず、検索アルゴリズムを使用して、削除するターゲットノードを見つけます。

ターゲットノードの左側(前の)ノードは、ターゲットノードの次のノードを指す必要があります-
LeftNode.next −> TargetNode.next;
これにより、ターゲットノードを指していたリンクが削除されます。ここで、次のコードを使用して、ターゲットノードが指しているものを削除します。
TargetNode.next −> NULL;
削除したノードを使用する必要があります。それをメモリに保持することができます。そうでない場合は、メモリの割り当てを解除して、ターゲットノードを完全に消去するだけです。

逆の操作
この操作は徹底的なものです。最後のノードがヘッドノードによってポイントされるようにし、リンクリスト全体を逆にする必要があります。
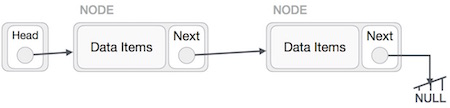
まず、リストの最後までトラバースします。NULLを指している必要があります。ここで、前のノードを指すようにします-
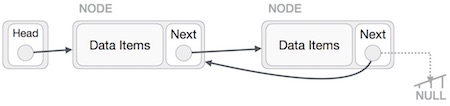
最後のノードが最後のノードではないことを確認する必要があります。したがって、最後のノードを指すヘッドノードのように見える一時ノードがいくつかあります。ここで、すべての左側のノードが前のノードを1つずつ指すようにします。
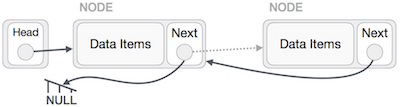
ヘッドノードが指すノード(最初のノード)を除いて、すべてのノードは前のノードを指し、新しい後継ノードにする必要があります。最初のノードはNULLを指します。

一時ノードを使用して、ヘッドノードが新しい最初のノードを指すようにします。
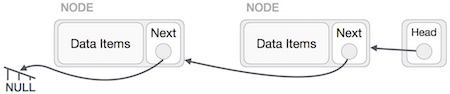
リンクリストが逆になります。Cプログラミング言語でのリンクリストの実装を確認するには、ここをクリックしてください。
二重リンクリストは、リンクリストのバリエーションであり、単一リンクリストと比較して、順方向と逆方向の両方の方法で簡単にナビゲーションできます。以下は、二重リンクリストの概念を理解するための重要な用語です。
Link −リンクリストの各リンクには、要素と呼ばれるデータを格納できます。
Next −リンクリストの各リンクには、Nextと呼ばれる次のリンクへのリンクが含まれています。
Prev −リンクリストの各リンクには、前と呼ばれる前のリンクへのリンクが含まれています。
LinkedList −リンクリストには、Firstと呼ばれる最初のリンクとLastと呼ばれる最後のリンクへの接続リンクが含まれています。
二重リンクリスト表現

上の図のように、以下は考慮すべき重要なポイントです。
二重リンクリストには、firstとlastというリンク要素が含まれています。
各リンクには、データフィールドとnextおよびprevと呼ばれる2つのリンクフィールドがあります。
各リンクは、次のリンクを使用して次のリンクにリンクされます。
各リンクは、前のリンクを使用して前のリンクにリンクされています。
最後のリンクは、リストの終わりを示すためにnullとしてリンクを運びます。
基本操作
以下は、リストでサポートされている基本的な操作です。
Insertion −リストの先頭に要素を追加します。
Deletion −リストの先頭にある要素を削除します。
Insert Last −リストの最後に要素を追加します。
Delete Last −リストの最後から要素を削除します。
Insert After −リストの項目の後に要素を追加します。
Delete −キーを使用してリストから要素を削除します。
Display forward −完全なリストを順方向に表示します。
Display backward −完全なリストを逆方向に表示します。
挿入操作
次のコードは、二重リンクリストの先頭での挿入操作を示しています。
例
//insert link at the first location
void insertFirst(int key, int data) {
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}削除操作
次のコードは、二重リンクリストの先頭での削除操作を示しています。
例
//delete first item
struct node* deleteFirst() {
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}操作終了時の挿入
次のコードは、二重リンクリストの最後の位置での挿入操作を示しています。
例
//insert link at the last location
void insertLast(int key, int data) {
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}Cプログラミング言語での実装を確認するには、ここをクリックしてください。
循環リンクリストは、最初の要素が最後の要素を指し、最後の要素が最初の要素を指すリンクリストのバリエーションです。単一リンクリストと二重リンクリストの両方を循環リンクリストにすることができます。
循環としての単一リンクリスト
単一リンクリストでは、最後のノードの次のポインタが最初のノードを指します。

循環としての二重リンクリスト
二重リンクリストでは、最後のノードの次のポインタが最初のノードを指し、最初のノードの前のポインタが最後のノードを指し、両方向に循環します。

上の図のように、以下は考慮すべき重要なポイントです。
最後のリンクの次は、単一リンクリストと二重リンクリストの両方の場合に、リストの最初のリンクを指します。
二重リンクリストの場合、最初のリンクの前はリストの最後を指します。
基本操作
以下は、循環リストでサポートされている重要な操作です。
insert −リストの先頭に要素を挿入します。
delete −リストの先頭から要素を削除します。
display −リストを表示します。
挿入操作
次のコードは、単一のリンクリストに基づく循環リンクリストへの挿入操作を示しています。
例
//insert link at the first location
void insertFirst(int key, int data) {
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data= data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}削除操作
次のコードは、単一のリンクリストに基づく循環リンクリストでの削除操作を示しています。
//delete first item
struct node * deleteFirst() {
//save reference to first link
struct node *tempLink = head;
if(head->next == head) {
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}ディスプレイリストの操作
次のコードは、循環リンクリストでのリストの表示操作を示しています。
//display the list
void printList() {
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}Cプログラミング言語での実装については、ここをクリックしてください。
スタックは抽象データ型(ADT)であり、ほとんどのプログラミング言語で一般的に使用されています。たとえば、カードのデッキやプレートの山など、実際のスタックのように動作するため、スタックと呼ばれます。

実際のスタックでは、一方の端でのみ操作が可能です。たとえば、カードやプレートはスタックの一番上からのみ配置または削除できます。同様に、Stack ADTは、すべてのデータ操作を一方の端でのみ許可します。いつでも、スタックの最上位要素にのみアクセスできます。
この機能により、LIFOデータ構造になります。LIFOは後入れ先出しの略です。ここでは、最後に配置(挿入または追加)された要素が最初にアクセスされます。スタック用語では、挿入操作はPUSH 操作と取り外し操作はと呼ばれます POP 操作。
スタック表現
次の図は、スタックとその操作を示しています-

スタックは、配列、構造体、ポインター、およびリンクリストを使用して実装できます。スタックは固定サイズのものでも、動的なサイズ変更の感覚がある場合もあります。ここでは、配列を使用してスタックを実装します。これにより、固定サイズのスタック実装になります。
基本操作
スタック操作には、スタックの初期化、使用、および非初期化が含まれる場合があります。これらの基本的なものとは別に、スタックは次の2つの主要な操作に使用されます-
push() −スタック上の要素をプッシュ(保存)します。
pop() −スタックから要素を削除(アクセス)します。
データがスタックにプッシュされるとき。
スタックを効率的に使用するには、スタックのステータスも確認する必要があります。同じ目的で、次の機能がスタックに追加されます-
peek() −スタックの最上位のデータ要素を削除せずに取得します。
isFull() −スタックがいっぱいかどうかを確認します。
isEmpty() −スタックが空かどうかを確認します。
常に、スタック上の最後のPUSHされたデータへのポインターを維持します。このポインタは常にスタックの最上位を表すため、top。ザ・top ポインタは、実際にスタックを削除せずに、スタックの最上位値を提供します。
まず、スタック関数をサポートする手順について学ぶ必要があります-
ピーク()
peek()関数のアルゴリズム-
begin procedure peek
return stack[top]
end procedureCプログラミング言語でのpeek()関数の実装-
Example
int peek() {
return stack[top];
}一杯()
isfull()関数のアルゴリズム-
begin procedure isfull
if top equals to MAXSIZE
return true
else
return false
endif
end procedureCプログラミング言語でのisfull()関数の実装-
Example
bool isfull() {
if(top == MAXSIZE)
return true;
else
return false;
}isempty()
isempty()関数のアルゴリズム-
begin procedure isempty
if top less than 1
return true
else
return false
endif
end procedureCプログラミング言語でのisempty()関数の実装は少し異なります。配列のインデックスは0から始まるため、topを-1で初期化します。したがって、topが0または-1を下回っているかどうかを確認して、スタックが空かどうかを判断します。これがコードです-
Example
bool isempty() {
if(top == -1)
return true;
else
return false;
}プッシュ操作
新しいデータ要素をスタックに配置するプロセスは、プッシュ操作と呼ばれます。プッシュ操作には一連のステップが含まれます-
Step 1 −スタックがいっぱいかどうかを確認します。
Step 2 −スタックがいっぱいの場合、エラーが発生して終了します。
Step 3 −スタックがいっぱいでない場合は、増分します top 次の空きスペースをポイントします。
Step 4 −topが指しているスタック位置にデータ要素を追加します。
Step 5 −成功を返します。
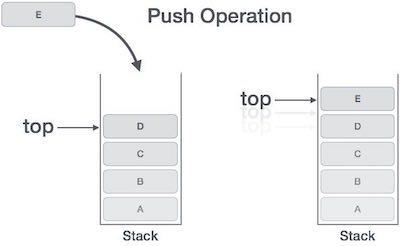
リンクリストを使用してスタックを実装する場合は、手順3でスペースを動的に割り当てる必要があります。
PUSH操作のアルゴリズム
プッシュ操作の簡単なアルゴリズムは、次のように導き出すことができます。
begin procedure push: stack, data
if stack is full
return null
endif
top ← top + 1
stack[top] ← data
end procedureこのアルゴリズムのCでの実装は、非常に簡単です。次のコードを参照してください-
Example
void push(int data) {
if(!isFull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}ポップオペレーション
スタックからコンテンツを削除しながらコンテンツにアクセスすることは、ポップ操作と呼ばれます。pop()操作の配列実装では、データ要素は実際には削除されず、代わりにtop次の値を指すために、スタック内のより低い位置にデクリメントされます。ただし、リンクリストの実装では、pop()は実際にデータ要素を削除し、メモリスペースの割り当てを解除します。
ポップ操作には、次の手順が含まれる場合があります-
Step 1 −スタックが空かどうかを確認します。
Step 2 −スタックが空の場合、エラーが発生して終了します。
Step 3 −スタックが空でない場合、データ要素にアクセスします。 top 指しています。
Step 4 −topの値を1減らします。
Step 5 −成功を返します。

ポップ演算のアルゴリズム
ポップ操作の簡単なアルゴリズムは、次のように導き出すことができます。
begin procedure pop: stack
if stack is empty
return null
endif
data ← stack[top]
top ← top - 1
return data
end procedureCでのこのアルゴリズムの実装は、次のとおりです。
Example
int pop(int data) {
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}Cプログラミング言語の完全なスタックプログラムについては、ここをクリックしてください。
算術式を書く方法は、 notation。算術式は、式の本質や出力を変更せずに、3つの異なるが同等の表記法で記述できます。これらの表記は-
- 中置記法
- プレフィックス(ポーランド語)表記
- 後置(逆ポーランド)表記
これらの表記は、式で演算子を使用する方法として名前が付けられています。この章でも同じことを学びます。
中置記法
式を書く infix 表記、たとえばa --b + c、ここで演算子が使用されます in-オペランド間。私たち人間は中置記法で読み、書き、話すのは簡単ですが、同じことはコンピューティングデバイスではうまくいきません。中置記法を処理するアルゴリズムは、時間とスペースの消費の点で困難でコストがかかる可能性があります。
プレフィックス表記
この表記では、演算子は prefixオペランドに編集されます。つまり、演算子はオペランドの前に書き込まれます。例えば、+ab。これは、中置記法と同等ですa + b。プレフィックス表記は、Polish Notation。
後置表記
この記譜スタイルは、 Reversed Polish Notation。この記譜法では、演算子はpostfixオペランドに編集されます。つまり、演算子はオペランドの後に記述されます。例えば、ab+。これは、中置記法と同等ですa + b。
次の表は、3つの表記すべての違いを簡単に示しています。
| シニア番号 | 中置記法 | プレフィックス表記 | 後置表記 |
|---|---|---|---|
| 1 | a + b | + ab | ab + |
| 2 | (a + b)∗ c | ∗ + abc | ab + c ∗ |
| 3 | a ∗(b + c) | ∗ a + bc | abc + ∗ |
| 4 | a / b + c / d | + / ab / cd | ab / cd / + |
| 5 | (a + b)∗(c + d) | ∗ + ab + cd | ab + cd + ∗ |
| 6 | ((a + b)∗ c)-d | -∗ + abcd | ab + c ∗ d- |
式の解析
すでに説明したように、中置記法を解析するアルゴリズムやプログラムを設計するのはあまり効率的な方法ではありません。代わりに、これらの中置記法は最初に接尾辞または接頭辞表記のいずれかに変換されてから計算されます。
算術式を解析するには、演算子の優先順位と結合性にも注意を払う必要があります。
優先順位
オペランドが2つの異なる演算子の間にある場合、どちらの演算子が最初にオペランドを取得するかは、他の演算子に対する演算子の優先順位によって決定されます。例-

乗算演算は加算よりも優先されるため、b * cが最初に評価されます。演算子の優先順位の表は後で提供されます。
結合性
結合性は、同じ優先順位を持つ演算子が式に現れる規則を表します。たとえば、式a + b − cでは、+と–の両方が同じ優先順位を持ち、式のどの部分が最初に評価されるかは、これらの演算子の結合性によって決定されます。ここでは、+と-の両方が結合性のままであるため、式は次のように評価されます。(a + b) − c。
優先順位と結合性は、式の評価の順序を決定します。以下は、演算子の優先順位と結合性の表(最高から最低)です。
| シニア番号 | オペレーター | 優先順位 | 結合性 |
|---|---|---|---|
| 1 | べき乗^ | 最高 | 右結合性 |
| 2 | 掛け算(∗)&割り算(/) | 2番目に高い | 左結合 |
| 3 | 足し算(+)&引き算(−) | 最低 | 左結合 |
上記の表は、演算子のデフォルトの動作を示しています。式の評価の任意の時点で、括弧を使用して順序を変更できます。例-
に a + b*c、表現部分 b*c最初に評価され、加算よりも乗算が優先されます。ここでは括弧を使用しますa + b 最初に評価されるように (a + b)*c。
接尾辞評価アルゴリズム
ここで、後置記法を評価する方法に関するアルゴリズムを見てみましょう。
Step 1 − scan the expression from left to right
Step 2 − if it is an operand push it to stack
Step 3 − if it is an operator pull operand from stack and perform operation
Step 4 − store the output of step 3, back to stack
Step 5 − scan the expression until all operands are consumed
Step 6 − pop the stack and perform operationCプログラミング言語での実装を確認するには、ここをクリックしてください。
キューは抽象的なデータ構造であり、スタックにいくぶん似ています。スタックとは異なり、キューは両端で開いています。一方の端は常にデータの挿入(エンキュー)に使用され、もう一方の端はデータの削除(デキュー)に使用されます。キューは先入れ先出し方式に従います。つまり、最初に格納されたデータ項目が最初にアクセスされます。

キューの実際の例は、車両が最初に進入し、最初に退出する単一車線の一方通行道路です。より現実的な例は、切符売り場やバス停の列として見ることができます。
キュー表現
キューにあることを理解したので、さまざまな理由で両端にアクセスします。以下の図は、キュー表現をデータ構造として説明しようとしています。

スタックの場合と同様に、キューは、配列、リンクリスト、ポインター、および構造を使用して実装することもできます。簡単にするために、1次元配列を使用してキューを実装します。
基本操作
キュー操作には、キューの初期化または定義、それを利用した後、メモリから完全に消去することが含まれる場合があります。ここでは、キューに関連する基本的な操作を理解しようとします-
enqueue() −アイテムをキューに追加(保存)します。
dequeue() −キューからアイテムを削除(アクセス)します。
上記のキュー操作を効率化するために必要な関数はこれ以上ありません。これらは-
peek() −キューの先頭にある要素を削除せずに取得します。
isfull() −キューがいっぱいかどうかを確認します。
isempty() −キューが空かどうかを確認します。
キューでは、常にデータをデキュー(またはアクセス)します。 front ポインタとキュー内のデータをクエリ(または保存)している間、私たちは助けを借ります rear ポインター。
まず、キューのサポート機能について学びましょう-
ピーク()
この関数は、でデータを確認するのに役立ちます frontキューの。peek()関数のアルゴリズムは次のとおりです-
Algorithm
begin procedure peek
return queue[front]
end procedureCプログラミング言語でのpeek()関数の実装-
Example
int peek() {
return queue[front];
}一杯()
単一次元配列を使用してキューを実装しているため、キューがいっぱいであると判断するために、リアポインタがMAXSIZEに到達するかどうかを確認するだけです。循環リンクリストでキューを維持する場合、アルゴリズムは異なります。isfull()関数のアルゴリズム-
Algorithm
begin procedure isfull
if rear equals to MAXSIZE
return true
else
return false
endif
end procedureCプログラミング言語でのisfull()関数の実装-
Example
bool isfull() {
if(rear == MAXSIZE - 1)
return true;
else
return false;
}isempty()
isempty()関数のアルゴリズム-
Algorithm
begin procedure isempty
if front is less than MIN OR front is greater than rear
return true
else
return false
endif
end procedureの値が front がMINまたは0未満の場合、キューがまだ初期化されていないため、空であることを示します。
これがCプログラミングコードです-
Example
bool isempty() {
if(front < 0 || front > rear)
return true;
else
return false;
}エンキュー操作
キューは2つのデータポインタを維持します。 front そして rear。したがって、その操作はスタックの操作よりも実装が比較的困難です。
データをキューにエンキュー(挿入)するには、次の手順を実行する必要があります-
Step 1 −キューがいっぱいかどうかを確認します。
Step 2 −キューがいっぱいの場合は、オーバーフローエラーを生成して終了します。
Step 3 −キューがいっぱいでない場合は、インクリメントします rear 次の空のスペースを指すポインタ。
Step 4 −後部が指しているキューの場所にデータ要素を追加します。
Step 5 −成功を返します。

場合によっては、予期しない状況に対処するために、キューが初期化されているかどうかを確認することもあります。
エンキュー操作のアルゴリズム
procedure enqueue(data)
if queue is full
return overflow
endif
rear ← rear + 1
queue[rear] ← data
return true
end procedureCプログラミング言語でのenqueue()の実装-
Example
int enqueue(int data)
if(isfull())
return 0;
rear = rear + 1;
queue[rear] = data;
return 1;
end procedureデキュー操作
キューからのデータへのアクセスは、2つのタスクのプロセスです。 frontアクセス後にデータをポイントして削除します。実行するには、次の手順を実行しますdequeue 操作-
Step 1 −キューが空かどうかを確認します。
Step 2 −キューが空の場合、アンダーフローエラーを生成して終了します。
Step 3 −キューが空でない場合は、次の場所のデータにアクセスします。 front 指しています。
Step 4 −インクリメント front 次に使用可能なデータ要素を指すポインタ。
Step 5 −成功を返します。
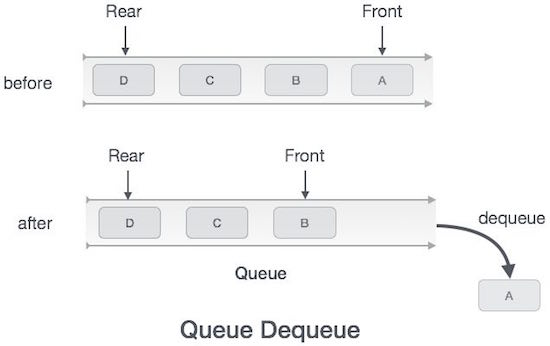
デキュー操作のアルゴリズム
procedure dequeue
if queue is empty
return underflow
end if
data = queue[front]
front ← front + 1
return true
end procedureCプログラミング言語でのdequeue()の実装-
Example
int dequeue() {
if(isempty())
return 0;
int data = queue[front];
front = front + 1;
return data;
}Cプログラミング言語の完全なキュープログラムについては、ここをクリックしてください。
線形検索は非常に単純な検索アルゴリズムです。このタイプの検索では、すべてのアイテムを1つずつ順次検索します。すべてのアイテムがチェックされ、一致するものが見つかった場合はその特定のアイテムが返されます。それ以外の場合は、データ収集が終了するまで検索が続行されます。

アルゴリズム
Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit擬似コード
procedure linear_search (list, value)
for each item in the list
if match item == value
return the item's location
end if
end for
end procedureCプログラミング言語での線形検索の実装については、ここをクリックしてください。
二分探索は、実行時の複雑さがΟ(log n)の高速検索アルゴリズムです。この検索アルゴリズムは、分割統治の原則に基づいて機能します。このアルゴリズムが正しく機能するためには、データ収集がソートされた形式である必要があります。
バイナリ検索では、コレクションの真ん中のアイテムを比較して特定のアイテムを検索します。一致する場合は、アイテムのインデックスが返されます。中央のアイテムがアイテムよりも大きい場合、アイテムは中央のアイテムの左側にあるサブ配列で検索されます。それ以外の場合、アイテムは中央のアイテムの右側のサブ配列で検索されます。このプロセスは、サブアレイのサイズがゼロになるまでサブアレイでも続行されます。
バイナリ検索はどのように機能しますか?
バイナリ検索が機能するためには、ターゲット配列をソートする必要があります。絵の例で二分探索のプロセスを学びます。以下はソートされた配列であり、バイナリ検索を使用して値31の場所を検索する必要があると仮定します。

まず、次の式を使用して配列の半分を決定します。
mid = low + (high - low) / 2これは、0 +(9-0)/ 2 = 4(整数値4.5)です。したがって、4は配列の中央です。

ここで、場所4に格納されている値を、検索されている値、つまり31と比較します。場所4の値は27であり、一致していません。値が27より大きく、配列が並べ替えられているため、ターゲット値が配列の上部にある必要があることもわかっています。

低値を中値+1に変更し、新しい中値を再度見つけます。
low = mid + 1
mid = low + (high - low) / 2私たちの新しいミッドは今7です。ロケーション7に格納されている値をターゲット値31と比較します。

場所7に格納されている値は一致していません。むしろ、私たちが探している値を超えています。したがって、値はこの場所から下部にある必要があります。

したがって、中間を再度計算します。今回は5です。

ロケーション5に保存されている値をターゲット値と比較します。一致していることがわかります。

目標値31は場所5に格納されていると結論付けます。
二分探索は検索可能な項目を半分にするため、比較の数が非常に少なくなります。
擬似コード
二分探索アルゴリズムの擬似コードは次のようになります-
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedureCプログラミング言語で配列を使用したバイナリ検索の実装については、ここをクリックしてください。
補間検索は、バイナリ検索の改良版です。この検索アルゴリズムは、必要な値のプロービング位置で機能します。このアルゴリズムが正しく機能するためには、データ収集がソートされた形式で均等に分散されている必要があります。
二分探索には、線形探索よりも時間の複雑さという大きな利点があります。線形検索の複雑さは最悪の場合Ο(n)ですが、バイナリ検索の複雑さはΟ(log n)です。
ターゲットデータの場所が事前にわかっている場合があります。たとえば、電話帳の場合、Morphiusの電話番号を検索する場合です。ここでは、名前が「M」で始まるメモリ空間に直接ジャンプできるため、線形検索やバイナリ検索でさえ遅いように見えます。
二分探索での位置付け
二分探索では、目的のデータが見つからない場合、リストの残りの部分は、下位と上位の2つの部分に分割されます。検索はどちらかで実行されます。




データがソートされている場合でも、バイナリ検索は目的のデータの位置を調べるために利用されません。
補間検索での位置プロービング
補間検索は、プローブ位置を計算することによって特定のアイテムを見つけます。最初、プローブ位置はコレクションの真ん中のアイテムの位置です。


一致する場合は、アイテムのインデックスが返されます。リストを2つの部分に分割するには、次の方法を使用します。
mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
where −
A = list
Lo = Lowest index of the list
Hi = Highest index of the list
A[n] = Value stored at index n in the list中央のアイテムがアイテムよりも大きい場合、プローブの位置は、中央のアイテムの右側のサブ配列で再度計算されます。それ以外の場合、アイテムは中央のアイテムの左側にあるサブ配列で検索されます。このプロセスは、サブアレイのサイズがゼロになるまでサブアレイでも続行されます。
補間検索アルゴリズムの実行時の複雑さは Ο(log (log n)) と比較して Ο(log n) 有利な状況でのBSTの。
アルゴリズム
これは既存のBSTアルゴリズムの即興であるため、位置プロービングを使用して「ターゲット」データ値インデックスを検索する手順について説明します。
Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.擬似コード
A → Array list
N → Size of A
X → Target Value
Procedure Interpolation_Search()
Set Lo → 0
Set Mid → -1
Set Hi → N-1
While X does not match
if Lo equals to Hi OR A[Lo] equals to A[Hi]
EXIT: Failure, Target not found
end if
Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
if A[Mid] = X
EXIT: Success, Target found at Mid
else
if A[Mid] < X
Set Lo to Mid+1
else if A[Mid] > X
Set Hi to Mid-1
end if
end if
End While
End ProcedureCプログラミング言語での補間検索の実装については、ここをクリックしてください。
ハッシュテーブルは、データを連想的に格納するデータ構造です。ハッシュテーブルでは、データは配列形式で格納され、各データ値には独自のインデックス値があります。目的のデータのインデックスがわかっている場合、データへのアクセスは非常に高速になります。
したがって、データのサイズに関係なく、挿入および検索操作が非常に高速なデータ構造になります。ハッシュテーブルは、記憶媒体として配列を使用し、ハッシュ手法を使用して、要素が挿入される、または配置されるインデックスを生成します。
ハッシュ
ハッシュは、キー値の範囲を配列のインデックスの範囲に変換する手法です。モジュロ演算子を使用して、キー値の範囲を取得します。サイズ20のハッシュテーブルの例を考えてみましょう。次のアイテムが格納されます。アイテムは(キー、値)形式です。

- (1,20)
- (2,70)
- (42,80)
- (4,25)
- (12,44)
- (14,32)
- (17,11)
- (13,78)
- (37,98)
| シニア番号 | キー | ハッシュ | 配列インデックス |
|---|---|---|---|
| 1 | 1 | 1%20 = 1 | 1 |
| 2 | 2 | 2%20 = 2 | 2 |
| 3 | 42 | 42%20 = 2 | 2 |
| 4 | 4 | 4%20 = 4 | 4 |
| 5 | 12 | 12%20 = 12 | 12 |
| 6 | 14 | 14%20 = 14 | 14 |
| 7 | 17 | 17%20 = 17 | 17 |
| 8 | 13 | 13%20 = 13 | 13 |
| 9 | 37 | 37%20 = 17 | 17 |
線形プロービング
ご覧のとおり、ハッシュ手法を使用して、すでに使用されている配列のインデックスを作成する場合があります。このような場合、空のセルが見つかるまで次のセルを調べることで、配列内の次の空の場所を検索できます。この手法は線形プロービングと呼ばれます。
| シニア番号 | キー | ハッシュ | 配列インデックス | 線形プロービング後、配列インデックス |
|---|---|---|---|---|
| 1 | 1 | 1%20 = 1 | 1 | 1 |
| 2 | 2 | 2%20 = 2 | 2 | 2 |
| 3 | 42 | 42%20 = 2 | 2 | 3 |
| 4 | 4 | 4%20 = 4 | 4 | 4 |
| 5 | 12 | 12%20 = 12 | 12 | 12 |
| 6 | 14 | 14%20 = 14 | 14 | 14 |
| 7 | 17 | 17%20 = 17 | 17 | 17 |
| 8 | 13 | 13%20 = 13 | 13 | 13 |
| 9 | 37 | 37%20 = 17 | 17 | 18 |
基本操作
以下は、ハッシュテーブルの基本的な主要な操作です。
Search −ハッシュテーブル内の要素を検索します。
Insert −ハッシュテーブルに要素を挿入します。
delete −ハッシュテーブルから要素を削除します。
DataItem
ハッシュテーブルで検索を実行するためのデータとキーを含むデータ項目を定義します。
struct DataItem {
int data;
int key;
};ハッシュ法
データ項目のキーのハッシュコードを計算するためのハッシュメソッドを定義します。
int hashCode(int key){
return key % SIZE;
}検索操作
要素を検索する場合は常に、渡されたキーのハッシュコードを計算し、そのハッシュコードを配列のインデックスとして使用して要素を見つけます。計算されたハッシュコードで要素が見つからない場合は、線形プロービングを使用して要素を先に進めます。
例
struct DataItem *search(int key) {
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}挿入操作
要素を挿入する場合は常に、渡されたキーのハッシュコードを計算し、そのハッシュコードを配列のインデックスとして使用してインデックスを見つけます。計算されたハッシュコードで要素が見つかった場合は、空の場所に線形プローブを使用します。
例
void insert(int key,int data) {
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}削除操作
要素を削除する場合は常に、渡されたキーのハッシュコードを計算し、そのハッシュコードを配列のインデックスとして使用してインデックスを見つけます。計算されたハッシュコードで要素が見つからない場合は、線形プロービングを使用して要素を先に進めます。見つかったら、ハッシュテーブルのパフォーマンスを維持するために、そこにダミーアイテムを格納します。
例
struct DataItem* delete(struct DataItem* item) {
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL) {
if(hashArray[hashIndex]->key == key) {
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}Cプログラミング言語でのハッシュ実装については、ここをクリックしてください。
並べ替えとは、特定の形式でデータを配置することです。並べ替えアルゴリズムは、特定の順序でデータを配置する方法を指定します。最も一般的な順序は、番号順または辞書式順序です。
並べ替えの重要性は、データが並べ替えられた方法で保存されている場合、データ検索を非常に高いレベルに最適化できるという事実にあります。並べ替えは、データをより読みやすい形式で表すためにも使用されます。以下は、実際のシナリオでの並べ替えの例の一部です。
Telephone Directory −電話帳には、名前でソートされた人の電話番号が格納されているため、名前を簡単に検索できます。
Dictionary −辞書には単語がアルファベット順に保存されているため、任意の単語を簡単に検索できます。
インプレースソートと非インプレースソート
ソートアルゴリズムでは、いくつかのデータ要素を比較および一時的に保存するために、追加のスペースが必要になる場合があります。これらのアルゴリズムは余分なスペースを必要とせず、ソートはインプレースで、またはたとえば配列自体の中で行われると言われています。これは呼ばれますin-place sorting。バブルソートは、インプレースソートの例です。
ただし、一部のソートアルゴリズムでは、プログラムはソートされる要素以上のスペースを必要とします。等しいかそれ以上のスペースを使用するソートはと呼ばれますnot-in-place sorting。マージソートは、インプレースソートの例です。
安定ソートと不安定ソート
ソートアルゴリズムは、コンテンツをソートした後、それらが表示される類似のコンテンツのシーケンスを変更しない場合、それは呼び出されます stable sorting。

ソートアルゴリズムが、コンテンツをソートした後、それらが表示される類似のコンテンツのシーケンスを変更する場合、それは呼び出されます unstable sorting。

アルゴリズムの安定性は、たとえばタプルのように、元の要素のシーケンスを維持したい場合に重要です。
適応型および非適応型のソートアルゴリズム
ソートされるリスト内のすでに「ソートされた」要素を利用する場合、ソートアルゴリズムは適応型であると言われます。つまり、ソースリストにすでに並べ替えられている要素がある場合に並べ替えるときに、適応アルゴリズムはこれを考慮に入れて、それらを並べ替えないようにします。
非適応アルゴリズムは、すでにソートされている要素を考慮しないアルゴリズムです。彼らは、すべての要素を強制的に並べ替えて、並べ替えを確認しようとします。
重要な用語
いくつかの用語は、一般的にソート手法を議論するときに造られます。ここにそれらの簡単な紹介があります-
注文の増加
値のシーケンスはにあると言われています increasing order、連続する要素が前の要素よりも大きい場合。たとえば、1、3、4、6、8、9は昇順で、次のすべての要素が前の要素よりも大きいためです。
注文の減少
値のシーケンスはにあると言われています decreasing order、連続する要素が現在の要素よりも小さい場合。たとえば、9、8、6、4、3、1は降順です。これは、次のすべての要素が前の要素よりも小さいためです。
増加しない注文
値のシーケンスはにあると言われています non-increasing order、連続する要素がシーケンス内の前の要素以下の場合。この順序は、シーケンスに重複する値が含まれている場合に発生します。たとえば、9、8、6、3、3、1は昇順ではありません。これは、次のすべての要素が(3の場合)以下であるが、前の要素よりも大きくないためです。
非減少注文
値のシーケンスはにあると言われています non-decreasing order、連続する要素がシーケンス内の前の要素以上の場合。この順序は、シーケンスに重複する値が含まれている場合に発生します。たとえば、1、3、3、6、8、9は降順ではありません。これは、次のすべての要素が(3の場合)以上、前の要素以上であるためです。
バブルソートは単純なソートアルゴリズムです。このソートアルゴリズムは比較ベースのアルゴリズムであり、隣接する要素の各ペアが比較され、要素が順番になっていない場合は要素が交換されます。このアルゴリズムは、平均および最悪の場合の複雑さがΟ(n 2)であるため、大規模なデータセットには適していません。n アイテムの数です。
バブルソートはどのように機能しますか?
例として、ソートされていない配列を取り上げます。バブルソートにはΟ(n 2)時間がかかるため、短く正確にしています。

バブルソートは最初の2つの要素から始まり、それらを比較してどちらが大きいかを確認します。

この場合、値33は14より大きいため、すでにソートされた場所にあります。次に、33と27を比較します。

27は33よりも小さいため、これら2つの値を交換する必要があります。

新しい配列は次のようになります-

次に、33と35を比較します。両方ともすでにソートされた位置にあることがわかります。

次に、次の2つの値、35と10に移動します。

その場合、10は35よりも小さいことがわかります。したがって、それらはソートされません。

これらの値を交換します。配列の最後に到達したことがわかります。1回の反復後、配列は次のようになります。

正確には、各反復後に配列がどのように見えるかを示しています。2回目の反復後は、次のようになります。

各反復の後、少なくとも1つの値が最後に移動することに注意してください。

そして、スワップが必要ない場合、バブルソートは配列が完全にソートされていることを学習します。

ここで、バブルソートのいくつかの実用的な側面を調べる必要があります。
アルゴリズム
私たちは仮定します list の配列です n要素。さらに、swap 関数は、指定された配列要素の値を交換します。
begin BubbleSort(list)
for all elements of list
if list[i] > list[i+1]
swap(list[i], list[i+1])
end if
end for
return list
end BubbleSort擬似コード
アルゴリズムでは、配列全体が完全に昇順でソートされていない限り、バブルソートが配列要素の各ペアを比較することがわかります。これにより、すべての要素がすでに昇順であるために配列をスワッピングする必要がなくなった場合など、いくつかの複雑な問題が発生する可能性があります。
問題を緩和するために、1つのフラグ変数を使用します swappedこれは、スワップが発生したかどうかを確認するのに役立ちます。スワップが発生しなかった場合、つまり配列をソートするためにそれ以上の処理が必要ない場合、配列はループから抜け出します。
BubbleSortアルゴリズムの擬似コードは次のように書くことができます-
procedure bubbleSort( list : array of items )
loop = list.count;
for i = 0 to loop-1 do:
swapped = false
for j = 0 to loop-1 do:
/* compare the adjacent elements */
if list[j] > list[j+1] then
/* swap them */
swap( list[j], list[j+1] )
swapped = true
end if
end for
/*if no number was swapped that means
array is sorted now, break the loop.*/
if(not swapped) then
break
end if
end for
end procedure return list実装
元のアルゴリズムとその即興の擬似コードで対処しなかったもう1つの問題は、反復のたびに、最大値が配列の最後に落ち着くということです。したがって、次の反復には、すでにソートされている要素を含める必要はありません。この目的のために、実装では、すでにソートされた値を回避するために内部ループを制限します。
Cプログラミング言語でのバブルソートの実装については、ここをクリックしてください。
これは、インプレース比較ベースのソートアルゴリズムです。ここでは、常にソートされるサブリストが維持されます。たとえば、配列の下部はソートされるように維持されます。このソートされたサブリストに「挿入」される要素は、適切な場所を見つけてから、そこに挿入する必要があります。したがって、名前は、insertion sort。
配列は順番に検索され、並べ替えられていないアイテムが移動され、並べ替えられたサブリスト(同じ配列内)に挿入されます。このアルゴリズムは、平均および最悪の場合の複雑さがΟ(n 2)であるため、大規模なデータセットには適していません。n アイテムの数です。
挿入ソートはどのように機能しますか?
例として、ソートされていない配列を取り上げます。

挿入ソートは最初の2つの要素を比較します。

14と33の両方がすでに昇順であることがわかります。今のところ、14はソートされたサブリストにあります。

挿入ソートは先に進み、33と27を比較します。

そして、33が正しい位置にないことがわかります。

33を27に交換します。また、ソートされたサブリストのすべての要素をチェックします。ここでは、ソートされたサブリストには要素14が1つしかなく、27は14より大きいことがわかります。したがって、ソートされたサブリストは、スワップ後もソートされたままになります。

これで、ソートされたサブリストに14と27が含まれます。次に、33と10を比較します。

これらの値はソートされた順序ではありません。

だから私たちはそれらを交換します。

ただし、スワッピングすると27と10がソートされなくなります。

したがって、それらも交換します。

ここでも、14と10がソートされていない順序で見つかります。

再度交換します。3回目の反復の終わりまでに、4つのアイテムのソートされたサブリストができました。

このプロセスは、ソートされていないすべての値がソートされたサブリストでカバーされるまで続きます。ここで、挿入ソートのプログラミングの側面をいくつか見ていきます。
アルゴリズム
これで、このソート手法がどのように機能するかについての全体像がわかったので、挿入ソートを実現するための簡単な手順を導き出すことができます。
Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the
value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted擬似コード
procedure insertionSort( A : array of items )
int holePosition
int valueToInsert
for i = 1 to length(A) inclusive do:
/* select value to be inserted */
valueToInsert = A[i]
holePosition = i
/*locate hole position for the element to be inserted */
while holePosition > 0 and A[holePosition-1] > valueToInsert do:
A[holePosition] = A[holePosition-1]
holePosition = holePosition -1
end while
/* insert the number at hole position */
A[holePosition] = valueToInsert
end for
end procedureCプログラミング言語での挿入ソートの実装については、ここをクリックしてください。
選択ソートは単純なソートアルゴリズムです。このソートアルゴリズムは、リストが左端のソートされた部分と右端のソートされていない部分の2つの部分に分割されるインプレース比較ベースのアルゴリズムです。最初は、ソートされた部分は空で、ソートされていない部分はリスト全体です。
ソートされていない配列から最小の要素が選択され、左端の要素と交換され、その要素がソートされた配列の一部になります。このプロセスは、ソートされていない配列境界を1要素右に移動し続けます。
このアルゴリズムは、平均および最悪の場合の複雑さがΟ(n 2)であるため、大規模なデータセットには適していません。n アイテムの数です。
選択ソートはどのように機能しますか?
次の図の配列を例として考えてみましょう。

ソートされたリストの最初の位置については、リスト全体が順番にスキャンされます。現在14が格納されている最初の位置で、リスト全体を検索し、10が最低値であることがわかります。

したがって、14を10に置き換えます。1回の反復の後、リストの最小値である10が、ソートされたリストの最初の位置に表示されます。

33が存在する2番目の位置では、リストの残りの部分を線形にスキャンし始めます。

14がリストの2番目に低い値であり、2番目に表示されるはずです。これらの値を交換します。

2回の反復の後、2つの最小値がソートされた方法で先頭に配置されます。

同じプロセスが、配列内の残りのアイテムに適用されます。
以下は、ソートプロセス全体の図解です。

それでは、選択ソートのプログラミングの側面をいくつか学びましょう。
アルゴリズム
Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted擬似コード
procedure selection sort
list : array of items
n : size of list
for i = 1 to n - 1
/* set current element as minimum*/
min = i
/* check the element to be minimum */
for j = i+1 to n
if list[j] < list[min] then
min = j;
end if
end for
/* swap the minimum element with the current element*/
if indexMin != i then
swap list[min] and list[i]
end if
end for
end procedureCプログラミング言語での選択ソートの実装については、ここをクリックしてください。
マージソートは、分割統治法に基づくソート手法です。最悪の場合の時間計算量はΟ(nlog n)であり、これは最も尊敬されているアルゴリズムの1つです。
マージソートは、最初に配列を等しい半分に分割し、次にそれらをソートされた方法で結合します。
マージソートはどのように機能しますか?
マージソートを理解するために、ソートされていない配列を次のように取ります。

マージソートは、アトミック値が達成されない限り、最初に配列全体を繰り返し等しい半分に分割することを知っています。ここでは、8つのアイテムの配列がサイズ4の2つの配列に分割されていることがわかります。

これにより、オリジナルのアイテムの表示順序は変更されません。次に、これら2つの配列を半分に分割します。

これらの配列をさらに分割すると、これ以上分割できない原子値が得られます。

今、私たちはそれらが分解されたのとまったく同じ方法でそれらを組み合わせます。これらのリストに記載されているカラーコードに注意してください。
最初に各リストの要素を比較し、次にそれらをソートされた方法で別のリストに結合します。14と33がソートされた位置にあることがわかります。27と10を比較し、2つの値のターゲットリストで最初に10を入力し、次に27を配置します。19と35の順序を変更しますが、42と44は順番に配置されます。

結合フェーズの次の反復では、2つのデータ値のリストを比較し、それらをすべてソートされた順序で配置して、見つかったデータ値のリストにマージします。

最終的なマージ後、リストは次のようになります-

ここで、マージソートのプログラミングの側面をいくつか学ぶ必要があります。
アルゴリズム
マージソートは、リストを分割できなくなるまで、リストを均等に分割し続けます。定義上、リスト内の要素が1つしかない場合は、並べ替えられます。次に、マージソートは、新しいリストもソートされたまま、小さいソート済みリストを結合します。
Step 1 − if it is only one element in the list it is already sorted, return.
Step 2 − divide the list recursively into two halves until it can no more be divided.
Step 3 − merge the smaller lists into new list in sorted order.擬似コード
ここで、マージソート関数の擬似コードを確認します。私たちのアルゴリズムが指摘しているように、2つの主要な機能-分割とマージ。
マージソートは再帰で機能し、同じように実装を確認します。
procedure mergesort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end if
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
end while
return c
end procedureCプログラミング言語でのマージソートの実装については、ここをクリックしてください。
シェルソートは非常に効率的なソートアルゴリズムであり、挿入ソートアルゴリズムに基づいています。このアルゴリズムは、小さい値が右端にあり、左端に移動する必要がある場合、挿入ソートの場合のように大きなシフトを回避します。
このアルゴリズムは、広く広がっている要素に対して挿入ソートを使用します。最初にそれらをソートし、次に間隔の狭い要素をソートします。この間隔は、interval。この間隔は、クヌースの式に基づいて次のように計算されます。
クヌースの公式
h = h * 3 + 1
where −
h is interval with initial value 1このアルゴリズムは、平均および最悪の場合の複雑さがΟ(n)であるため、中規模のデータセットに対して非常に効率的です。 n アイテムの数です。
シェルソートはどのように機能しますか?
次の例を考えて、シェルソートがどのように機能するかを理解しましょう。前の例で使用したのと同じ配列を使用します。この例と理解を容易にするために、4の間隔を取ります。4つの位置の間隔にあるすべての値の仮想サブリストを作成します。ここで、これらの値は{35、14}、{33、19}、{42、27}および{10、44}です。

各サブリストの値を比較し、(必要に応じて)元の配列にスワップします。この手順の後、新しい配列は次のようになります。

次に、間隔2を取り、このギャップによって2つのサブリスト({14、27、35、42}、{19、10、33、44})が生成されます。

必要に応じて、元の配列の値を比較して交換します。このステップの後、配列は次のようになります-

最後に、値1の間隔を使用して配列の残りの部分を並べ替えます。シェルソートでは、挿入ソートを使用して配列をソートします。
以下は段階的な描写です-

残りの配列をソートするのに必要なスワップは4つだけであることがわかります。
アルゴリズム
以下は、シェルソートのアルゴリズムです。
Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted擬似コード
以下は、シェルソートの擬似コードです。
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval] >= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner - interval
end while
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedureCプログラミング言語でのシェルソートの実装については、ここをクリックしてください。
シェルソートは非常に効率的なソートアルゴリズムであり、挿入ソートアルゴリズムに基づいています。このアルゴリズムは、小さい値が右端にあり、左端に移動する必要がある場合、挿入ソートの場合のように大きなシフトを回避します。
このアルゴリズムは、広く広がっている要素に対して挿入ソートを使用します。最初にそれらをソートし、次に間隔の狭い要素をソートします。この間隔は、interval。この間隔は、クヌースの式に基づいて次のように計算されます。
クヌースの公式
h = h * 3 + 1
where −
h is interval with initial value 1このアルゴリズムの平均および最悪の場合の複雑さは、最もよく知られているギャップシーケンスがΟ(n)に依存するため、このアルゴリズムは中規模のデータセットに対して非常に効率的です。ここで、nはアイテムの数です。そして、最悪の場合のスペースの複雑さはO(n)です。
シェルソートはどのように機能しますか?
次の例を考えて、シェルソートがどのように機能するかを理解しましょう。前の例で使用したのと同じ配列を使用します。この例と理解を容易にするために、4の間隔を取ります。4つの位置の間隔にあるすべての値の仮想サブリストを作成します。ここで、これらの値は{35、14}、{33、19}、{42、27}および{10、44}です。

各サブリストの値を比較し、(必要に応じて)元の配列にスワップします。この手順の後、新しい配列は次のようになります。

次に、間隔を1にすると、このギャップによって2つのサブリスト({14、27、35、42}、{19、10、33、44})が生成されます。

必要に応じて、元の配列の値を比較して交換します。このステップの後、配列は次のようになります-

最後に、値1の間隔を使用して配列の残りの部分を並べ替えます。シェルソートでは、挿入ソートを使用して配列をソートします。
以下は段階的な描写です-

残りの配列をソートするのに必要なスワップは4つだけであることがわかります。
アルゴリズム
以下は、シェルソートのアルゴリズムです。
Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted擬似コード
以下は、シェルソートの擬似コードです。
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval] >= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner - interval
end while
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedureCプログラミング言語でのシェルソートの実装については、ここをクリックしてください。
クイックソートは非常に効率的なソートアルゴリズムであり、データの配列をより小さな配列に分割することに基づいています。大きな配列は2つの配列に分割され、そのうちの1つは指定された値よりも小さい値、たとえばピボットを保持します。これに基づいて分割が行われ、もう1つの配列はピボット値よりも大きい値を保持します。
クイックソートは配列を分割してから、それ自体を2回再帰的に呼び出して、結果の2つのサブ配列をソートします。このアルゴリズムは、平均および最悪の場合の複雑さがそれぞれO(nLogn)およびimage.png(n 2)であるため、大規模なデータセットに対して非常に効率的です。
クイックソートでのパーティション
次のアニメーション表現は、配列内のピボット値を見つける方法を説明しています。

ピボット値は、リストを2つの部分に分割します。そして再帰的に、すべてのリストに1つの要素のみが含まれるまで、各サブリストのピボットを見つけます。
クイックソートピボットアルゴリズム
クイックソートでのパーティショニングの理解に基づいて、次のようなアルゴリズムを作成してみましょう。
Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivotクイックソートピボット擬似コード
上記のアルゴリズムの擬似コードは、次のように導出できます。
function partitionFunc(left, right, pivot)
leftPointer = left
rightPointer = right - 1
while True do
while A[++leftPointer] < pivot do
//do-nothing
end while
while rightPointer > 0 && A[--rightPointer] > pivot do
//do-nothing
end while
if leftPointer >= rightPointer
break
else
swap leftPointer,rightPointer
end if
end while
swap leftPointer,right
return leftPointer
end functionクイックソートアルゴリズム
ピボットアルゴリズムを再帰的に使用すると、可能なパーティションが小さくなります。次に、各パーティションはクイックソートのために処理されます。クイックソートの再帰的アルゴリズムを次のように定義します-
Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursivelyクイックソート擬似コード
さらに詳しく知るために、クイックソートアルゴリズムの擬似コードを見てみましょう-
procedure quickSort(left, right)
if right-left <= 0
return
else
pivot = A[right]
partition = partitionFunc(left, right, pivot)
quickSort(left,partition-1)
quickSort(partition+1,right)
end if
end procedureCプログラミング言語でのクイックソートの実装については、ここをクリックしてください。
グラフは、オブジェクトのペアがリンクで接続されているオブジェクトのセットを図で表したものです。相互接続されたオブジェクトは、次のように呼ばれるポイントで表されます。vertices、および頂点を接続するリンクは呼び出されます edges。
正式には、グラフはセットのペアです (V, E)、 どこ V 頂点のセットであり、 Eは、頂点のペアを接続するエッジのセットです。次のグラフを見てください-
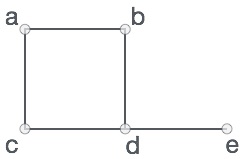
上のグラフでは、
V = {a、b、c、d、e}
E = {ab、ac、bd、cd、de}
グラフのデータ構造
数学的なグラフは、データ構造で表すことができます。頂点の配列とエッジの2次元配列を使用してグラフを表すことができます。先に進む前に、いくつかの重要な用語をよく理解しましょう。
Vertex−グラフの各ノードは頂点として表されます。次の例では、ラベルの付いた円は頂点を表しています。したがって、AからGは頂点です。次の図に示すように、配列を使用してそれらを表すことができます。ここで、Aはインデックス0で識別できます。Bはインデックス1を使用して識別できます。
Edge−エッジは、2つの頂点間のパスまたは2つの頂点間の線を表します。次の例では、AからB、BからCなどの線がエッジを表しています。次の図に示すように、2次元配列を使用して配列を表すことができます。ここで、ABは行0、列1で1として、BCは行1、列2で1として表すことができ、他の組み合わせは0のままにします。
Adjacency− 2つのノードまたは頂点がエッジを介して相互に接続されている場合、それらは隣接しています。次の例では、BはAに隣接し、CはBに隣接します。
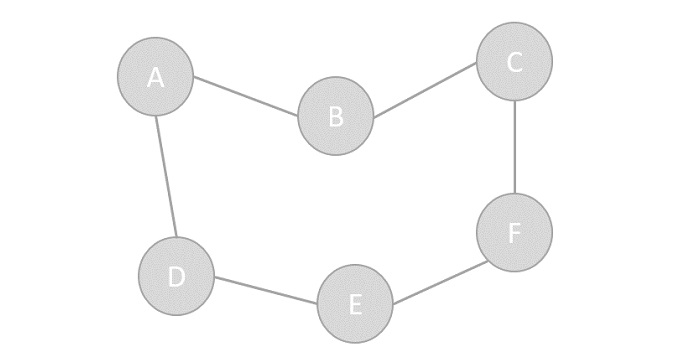
Path−パスは、2つの頂点間の一連のエッジを表します。次の例では、ABCDはAからDへのパスを表します。
基本操作
グラフの基本的な主な操作は次のとおりです-
Add Vertex −グラフに頂点を追加します。
Add Edge −グラフの2つの頂点の間にエッジを追加します。
Display Vertex −グラフの頂点を表示します。
グラフの詳細については、グラフ理論チュートリアルをお読みください。次の章では、グラフのトラバースについて学習します。
深さ優先探索(DFS)アルゴリズムは、グラフを深さ方向に移動し、スタックを使用して、反復で行き止まりが発生したときに、次の頂点を取得して検索を開始することを記憶します。

上記の例のように、DFSアルゴリズムは、最初にSからA、D、G、E、B、次にF、最後にCに移動します。次のルールを採用しています。
Rule 1−隣接する未訪問の頂点にアクセスします。訪問済みとしてマークします。表示します。スタックにプッシュします。
Rule 2−隣接する頂点が見つからない場合は、スタックから頂点をポップアップします。(隣接する頂点がないスタックからすべての頂点がポップアップ表示されます。)
Rule 3 −スタックが空になるまで、ルール1とルール2を繰り返します。
| ステップ | トラバーサル | 説明 |
|---|---|---|
| 1 |

|
スタックを初期化します。 |
| 2 |

|
マーク S訪問したとおりにスタックに置きます。からの未訪問の隣接ノードを探索しますS。3つのノードがあり、それらのいずれかを選択できます。この例では、ノードをアルファベット順に取り上げます。 |
| 3 |

|
マーク A訪問したとおりにスタックに置きます。Aから未訪問の隣接ノードを探索します。両方S そして D に隣接しています A ただし、未訪問のノードのみを対象としています。 |
| 4 |

|
訪問 D訪問済みとしてマークし、スタックに置きます。ここに、B そして C 隣接するノード Dそして両方とも訪問されていません。ただし、ここでもアルファベット順に選択します。 |
| 5 |

|
我々が選択しました B、訪問済みとしてマークし、スタックに置きます。ここにB未訪問の隣接ノードはありません。だから、私たちはポップしますB スタックから。 |
| 6 |

|
スタックトップが前のノードに戻っているかどうかを確認し、未訪問のノードがあるかどうかを確認します。ここで、D スタックの一番上になります。 |
| 7 |

|
訪問されていない隣接ノードのみが D です C今。だから私たちは訪問しますC、訪問済みとしてマークし、スタックに置きます。 |
なので C未訪問の隣接ノードがないため、未訪問の隣接ノードがあるノードが見つかるまでスタックをポップし続けます。この場合、何もありません。スタックが空になるまでポップし続けます。
Cプログラミング言語でのこのアルゴリズムの実装について知るには、ここをクリックしてください。
幅優先探索(BFS)アルゴリズムは、グラフを横方向に移動し、キューを使用して、反復で行き止まりが発生したときに、次の頂点を取得して検索を開始することを忘れないようにします。

上記の例のように、BFSアルゴリズムは、最初にAからB、E、F、次にC、G、最後にDに移動します。次のルールを採用しています。
Rule 1−隣接する未訪問の頂点にアクセスします。訪問済みとしてマークします。表示します。キューに挿入します。
Rule 2 −隣接する頂点が見つからない場合は、最初の頂点をキューから削除します。
Rule 3 −キューが空になるまで、ルール1とルール2を繰り返します。
| ステップ | トラバーサル | 説明 |
|---|---|---|
| 1 |

|
キューを初期化します。 |
| 2 |
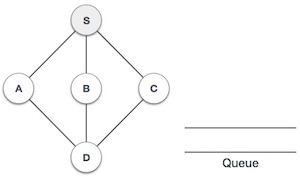
|
私たちは訪問から始めます S (開始ノード)、訪問済みとしてマークします。 |
| 3 |

|
次に、訪問されていない隣接ノードが S。この例では、3つのノードがありますが、アルファベット順に選択しますA、訪問済みとしてマークし、キューに入れます。 |
| 4 |

|
次に、からの未訪問の隣接ノード S です B。訪問済みとしてマークし、キューに入れます。 |
| 5 |

|
次に、からの未訪問の隣接ノード S です C。訪問済みとしてマークし、キューに入れます。 |
| 6 |

|
さて、 S未訪問の隣接ノードはありません。だから、私たちはデキューして見つけますA。 |
| 7 |

|
から A 我々は持っています D未訪問の隣接ノードとして。訪問済みとしてマークし、キューに入れます。 |
この段階では、マークされていない(訪問されていない)ノードはありません。しかし、アルゴリズムに従って、すべての未訪問ノードを取得するためにデキューを続けます。キューが空になると、プログラムは終了します。
Cプログラミング言語でのこのアルゴリズムの実装はここで見ることができます。
ツリーは、エッジで接続されたノードを表します。具体的には、二分木または二分探索木について説明します。
バイナリツリーは、データストレージの目的で使用される特別なデータ構造です。二分木には、各ノードが最大2つの子を持つことができるという特別な条件があります。バイナリツリーには、検索がソートされた配列と同じくらい高速であり、挿入または削除操作がリンクリストと同じくらい高速であるため、順序付き配列とリンクリストの両方の利点があります。

重要な用語
以下は、ツリーに関する重要な用語です。
Path −パスは、ツリーのエッジに沿ったノードのシーケンスを指します。
Root−ツリーの最上部にあるノードはルートと呼ばれます。ツリーごとに1つのルートと、ルートノードから任意のノードへのパスが1つだけあります。
Parent −ルートノードを除くすべてのノードには、親と呼ばれるノードの上方に1つのエッジがあります。
Child −エッジで下向きに接続された特定のノードの下のノードは、子ノードと呼ばれます。
Leaf −子ノードを持たないノードをリーフノードと呼びます。
Subtree −サブツリーはノードの子孫を表します。
Visiting −訪問とは、制御がノード上にあるときにノードの値をチェックすることを指します。
Traversing −トラバースとは、特定の順序でノードを通過することを意味します。
Levels−ノードのレベルは、ノードの生成を表します。ルートノードがレベル0の場合、次の子ノードはレベル1にあり、孫はレベル2にあり、以下同様に続きます。
keys −キーは、ノードの検索操作が実行されるノードの値を表します。
二分探索木表現
二分探索木は特別な振る舞いを示します。ノードの左の子はその親の値よりも小さい値である必要があり、ノードの右の子はその親の値よりも大きい値である必要があります。

ノードオブジェクトを使用してツリーを実装し、参照を介してそれらを接続します。
ツリーノード
ツリーノードを作成するコードは、以下のコードのようになります。データ部分と、その左右の子ノードへの参照があります。
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};ツリーでは、すべてのノードが共通の構成を共有します。
BSTの基本操作
二分探索木データ構造で実行できる基本的な操作は次のとおりです。
Insert −ツリーに要素を挿入/ツリーを作成します。
Search −ツリー内の要素を検索します。
Preorder Traversal −事前注文方式でツリーをトラバースします。
Inorder Traversal −ツリーを順番にトラバースします。
Postorder Traversal −ポストオーダー方式でツリーをトラバースします。
この章では、ツリー構造の作成(挿入)とツリー内のデータ項目の検索について学習します。次の章では、ツリー走査方法について学習します。
挿入操作
最初の挿入でツリーが作成されます。その後、要素を挿入するときは常に、最初にその適切な場所を見つけます。ルートノードから検索を開始し、データがキー値よりも小さい場合は、左側のサブツリーで空の場所を検索し、データを挿入します。それ以外の場合は、右側のサブツリーで空の場所を検索し、データを挿入します。
アルゴリズム
If root is NULL
then create root node
return
If root exists then
compare the data with node.data
while until insertion position is located
If data is greater than node.data
goto right subtree
else
goto left subtree
endwhile
insert data
end If実装
挿入関数の実装は次のようになります-
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty, create root node
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}
//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}検索操作
要素を検索する場合は常に、ルートノードから検索を開始し、データがキー値よりも小さい場合は、左側のサブツリーで要素を検索します。それ以外の場合は、右側のサブツリーで要素を検索します。各ノードで同じアルゴリズムに従います。
アルゴリズム
If root.data is equal to search.data
return root
else
while data not found
If data is greater than node.data
goto right subtree
else
goto left subtree
If data found
return node
endwhile
return data not found
end ifこのアルゴリズムの実装は次のようになります。
struct node* search(int data) {
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data) {
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}
//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
return current;
}
}二分探索木のデータ構造の実装については、ここをクリックしてください。
トラバーサルは、ツリーのすべてのノードにアクセスするプロセスであり、それらの値も出力する場合があります。すべてのノードはエッジ(リンク)を介して接続されているため、常にルート(ヘッド)ノードから開始します。つまり、ツリー内のノードにランダムにアクセスすることはできません。ツリーをトラバースするために使用する3つの方法があります-
- インオーダートラバーサル
- トラバーサルの事前注文
- 注文後のトラバーサル
通常、ツリーをトラバースして、ツリー内の特定のアイテムまたはキーを検索または検索したり、ツリーに含まれるすべての値を出力したりします。
インオーダートラバーサル
このトラバーサル方法では、最初に左側のサブツリーにアクセスし、次にルートにアクセスし、次に右側のサブツリーにアクセスします。すべてのノードがサブツリー自体を表す場合があることを常に覚えておく必要があります。
二分木がトラバースされる場合 in-order、出力は、ソートされたキー値を昇順で生成します。

から始めます A、および順序どおりの走査に続いて、左側のサブツリーに移動します B。 Bまた、順番にトラバースされます。このプロセスは、すべてのノードにアクセスするまで続きます。このツリーの順序通りのトラバーサルの出力は次のようになります-
D → B → E → A → F → C → G
アルゴリズム
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.トラバーサルの事前注文
このトラバーサル方法では、最初にルートノードにアクセスし、次に左側のサブツリーにアクセスし、最後に右側のサブツリーにアクセスします。

から始めます A、および事前注文トラバーサルに続いて、最初に訪問します A それ自体を選択してから、左側のサブツリーに移動します B。 Bプレオーダーもトラバースされます。このプロセスは、すべてのノードにアクセスするまで続きます。このツリーのプレオーダートラバーサルの出力は次のようになります-
A → B → D → E → C → F → G
アルゴリズム
Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.注文後のトラバーサル
このトラバーサル方法では、ルートノードが最後にアクセスされるため、この名前が付けられます。最初に左側のサブツリーをトラバースし、次に右側のサブツリーをトラバースし、最後にルートノードをトラバースします。

から始めます A、およびポストオーダートラバーサルに続いて、最初に左側のサブツリーにアクセスします B。 B注文後にもトラバースされます。このプロセスは、すべてのノードにアクセスするまで続きます。このツリーのポストオーダートラバーサルの出力は次のようになります-
D → E → B → F → G → C → A
アルゴリズム
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.ツリートラバースのC実装を確認するには、ここをクリックしてください。
二分探索木(BST)は、すべてのノードが以下のプロパティに従うツリーです。
左側のサブツリーのキーの値は、その親(ルート)ノードのキーの値よりも小さくなっています。
右側のサブツリーのキーの値は、その親(ルート)ノードのキーの値以上です。
したがって、BSTはすべてのサブツリーを2つのセグメントに分割します。左側のサブツリーと右側のサブツリーであり、次のように定義できます。
left_subtree (keys) < node (key) ≤ right_subtree (keys)表現
BSTは、BSTプロパティを維持するように配置されたノードのコレクションです。各ノードには、キーと関連する値があります。検索中に、目的のキーがBSTのキーと比較され、見つかった場合は、関連付けられた値が取得されます。
以下はBSTの図解です-

ルートノードキー(27)には、左側のサブツリーに値の小さいキーがすべてあり、右側のサブツリーに値の大きいキーがあることがわかります。
基本操作
ツリーの基本的な操作は次のとおりです-
Search −ツリー内の要素を検索します。
Insert −ツリーに要素を挿入します。
Pre-order Traversal −事前注文方式でツリーをトラバースします。
In-order Traversal −ツリーを順番にトラバースします。
Post-order Traversal −ポストオーダー方式でツリーをトラバースします。
ノード
いくつかのデータ、その左右の子ノードへの参照を持つノードを定義します。
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};検索操作
要素を検索する場合は常に、ルートノードから検索を開始してください。次に、データがキー値よりも小さい場合は、左側のサブツリーで要素を検索します。それ以外の場合は、右側のサブツリーで要素を検索します。各ノードで同じアルゴリズムに従います。
アルゴリズム
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
} //else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
}
return current;
}挿入操作
要素を挿入するときは常に、最初にその適切な場所を見つけます。ルートノードから検索を開始し、データがキー値よりも小さい場合は、左側のサブツリーで空の場所を検索し、データを挿入します。それ以外の場合は、右側のサブツリーで空の場所を検索し、データを挿入します。
アルゴリズム
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
} //go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}二分探索木への入力がソートされた(昇順または降順)方法で来る場合はどうなりますか?このようになります-

BSTの最悪の場合のパフォーマンスは、線形探索アルゴリズム、つまりΟ(n)に最も近いことが観察されています。リアルタイムデータでは、データパターンとその頻度を予測することはできません。そのため、既存のBSTのバランスを取る必要が生じます。
彼らの発明者にちなんで名付けられました Adelson、 Velski & Landis、 AVL trees高さバランス二分探索木です。AVLツリーは、左右のサブツリーの高さをチェックし、差が1以下であることを確認します。この差は、Balance Factor。
ここでは、最初のツリーのバランスが取れていて、次の2つのツリーのバランスが取れていないことがわかります。
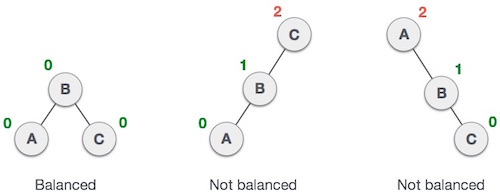
2番目のツリーでは、の左側のサブツリー C の高さは2で、右側のサブツリーの高さは0なので、差は2です。3番目のツリーでは、の右側のサブツリーは A高さが2で、左が欠落しているため、0であり、差は再び2です。AVLツリーでは、差(バランス係数)を1のみにすることができます。
BalanceFactor = height(left-sutree) − height(right-sutree)左右のサブツリーの高さの差が1より大きい場合、ツリーはいくつかの回転手法を使用してバランスが取られます。
AVLローテーション
バランスを取るために、AVLツリーは次の4種類のローテーションを実行できます-
- 左回転
- 右回転
- 左右回転
- 左右回転
最初の2回転は1回転で、次の2回転は2回転です。不均衡な木を作るには、少なくとも高さ2の木が必要です。この単純な木で、それらを1つずつ理解しましょう。
左回転
ツリーが不均衡になった場合、ノードが右側のサブツリーの右側のサブツリーに挿入されると、1回の左回転を実行します-

この例では、ノード AAの右側のサブツリーの右側のサブツリーにノードが挿入されると、バランスが崩れます。左回転を行うA Bの左側のサブツリー。
右回転
左側のサブツリーの左側のサブツリーにノードが挿入されると、AVLツリーが不均衡になる可能性があります。次に、ツリーを右に回転させる必要があります。

示されているように、不均衡なノードは、右回転を実行することにより、左の子の右の子になります。
左右回転
二重回転は、すでに説明したバージョンの回転の少し複雑なバージョンです。それらをよりよく理解するために、ローテーション中に実行される各アクションに注意する必要があります。まず、左右回転の実行方法を確認しましょう。左右回転は、左回転とそれに続く右回転の組み合わせです。
| 状態 | アクション |
|---|---|

|
左側のサブツリーの右側のサブツリーにノードが挿入されました。これはC不均衡なノード。これらのシナリオにより、AVLツリーは左右に回転します。 |

|
まず、の左サブツリーで左回転を実行します C。これはA、の左側のサブツリー B。 |

|
ノード C はまだ不均衡ですが、現在は、左サブツリーの左サブツリーが原因です。 |

|
木を右回転させて、 B このサブツリーの新しいルートノード。 C これで、独自の左側のサブツリーの右側のサブツリーになります。 |

|
これで、ツリーのバランスが取れました。 |
左右回転
二重回転の2番目のタイプは、右左回転です。これは、右回転とそれに続く左回転の組み合わせです。
| 状態 | アクション |
|---|---|

|
右側のサブツリーの左側のサブツリーにノードが挿入されました。これはA、バランス係数2の不平衡ノード。 |

|
まず、右回転を行います C ノード、作成 C 独自の左側のサブツリーの右側のサブツリー B。さて、B の正しいサブツリーになります A。 |

|
ノード A 右サブツリーの右サブツリーのためにまだ不均衡であり、左回転が必要です。 |

|
左回転は B サブツリーの新しいルートノード。 A 右側のサブツリーの左側のサブツリーになります B。 |

|
これで、ツリーのバランスが取れました。 |
スパニングツリーはグラフGのサブセットであり、すべての頂点が最小数のエッジで覆われています。したがって、スパニングツリーにはサイクルがなく、切断することはできません。
この定義により、すべての接続された無向グラフGには少なくとも1つのスパニングツリーがあるという結論を導き出すことができます。切断されたグラフには、すべての頂点にスパンできないため、スパニングツリーはありません。

1つの完全グラフから3つのスパニングツリーが見つかりました。完全な無向グラフは最大値を持つことができますnn-2 スパニングツリーの数、ここで nノードの数です。上記の例では、n is 3, したがって、 33−2 = 3 スパニングツリーが可能です。
スパニングツリーの一般的なプロパティ
これで、1つのグラフに複数のスパニングツリーを含めることができることがわかりました。以下は、グラフG −に接続されたスパニングツリーのいくつかのプロパティです。
接続されたグラフGは、複数の全域木を持つことができます。
グラフGのすべての可能な全域木は、同じ数のエッジと頂点を持っています。
スパニングツリーにはサイクル(ループ)がありません。
スパニングツリーから1つのエッジを削除すると、グラフが切断されます。つまり、スパニングツリーは minimally connected。
スパニングツリーに1つのエッジを追加すると、回路またはループが作成されます。つまり、スパニングツリーは次のようになります。 maximally acyclic。
スパニングツリーの数学的特性
スパニングツリーには n-1 エッジ、ここで n はノード(頂点)の数です。
完全グラフから、最大値を削除することにより e - n + 1 エッジ、スパニングツリーを構築できます。
完全グラフは最大値を持つことができます nn-2 スパニングツリーの数。
したがって、スパニングツリーは接続されたグラフGのサブセットであり、切断されたグラフにはスパニングツリーがないと結論付けることができます。
スパニングツリーの適用
スパニングツリーは基本的に、グラフ内のすべてのノードを接続するための最小パスを見つけるために使用されます。スパニングツリーの一般的な用途は次のとおりです。
Civil Network Planning
Computer Network Routing Protocol
Cluster Analysis
小さな例を通してこれを理解しましょう。都市ネットワークを巨大なグラフと考えてください。現在、最小限の回線ですべての都市ノードに接続できるように電話回線を展開することを計画しています。ここで、スパニングツリーが思い浮かびます。
最小スパニングツリー(MST)
加重グラフでは、最小全域木は、同じグラフの他のすべての全域木よりも最小の重みを持つ全域木です。実際の状況では、この重みは、距離、混雑、交通負荷、またはエッジに示される任意の値として測定できます。
最小スパニングツリーアルゴリズム
ここでは、2つの最も重要なスパニングツリーアルゴリズムについて学習します。
クラスカルのアルゴリズム
プリムのアルゴリズム
どちらも欲張りアルゴリズムです。
ヒープは、バランス二分木データ構造の特殊なケースであり、ルートノードキーがその子と比較され、それに応じて配置されます。場合α 子ノードがあります β 次に−
key(α)≥key(β)
親の値が子の値よりも大きいため、このプロパティは次のように生成します。 Max Heap。この基準に基づいて、ヒープには2つのタイプがあります-
For Input → 35 33 42 10 14 19 27 44 26 31Min-Heap −ルートノードの値がその子のいずれか以下である場合。
Max-Heap −ルートノードの値がその子のいずれか以上である場合。

両方のツリーは、同じ入力と到着順序を使用して構築されます。
最大ヒープ構築アルゴリズム
同じ例を使用して、最大ヒープがどのように作成されるかを示します。最小ヒープを作成する手順は似ていますが、最大値ではなく最小値を使用します。
一度に1つの要素を挿入することにより、最大ヒープのアルゴリズムを導出します。いつでも、ヒープはそのプロパティを維持する必要があります。挿入中、すでにヒープ化されたツリーにノードを挿入していることも前提としています。
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.Note −最小ヒープ構築アルゴリズムでは、親ノードの値が子ノードの値よりも小さいと予想されます。
アニメーションイラストでマックスヒープの構成を理解しましょう。以前に使用したものと同じ入力サンプルを検討します。

最大ヒープ削除アルゴリズム
最大ヒープから削除するアルゴリズムを導き出しましょう。最大(または最小)ヒープの削除は、最大(または最小)値を削除するために常にルートで行われます。
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.
一部のコンピュータープログラミング言語では、モジュールまたは関数がそれ自体を呼び出すことができます。この手法は再帰として知られています。再帰では、関数α 自分自身を直接呼び出すか、関数を呼び出します β これにより、元の関数が呼び出されます α。関数α 再帰関数と呼ばれます。
Example −それ自体を呼び出す関数。
int function(int value) {
if(value < 1)
return;
function(value - 1);
printf("%d ",value);
}Example −別の関数を呼び出す関数で、別の関数が再度呼び出します。
int function1(int value1) {
if(value1 < 1)
return;
function2(value1 - 1);
printf("%d ",value1);
}
int function2(int value2) {
function1(value2);
}プロパティ
再帰関数は、ループのように無限に進む可能性があります。再帰関数の無限の実行を回避するために、再帰関数が持つ必要のある2つのプロパティがあります-
Base criteria −この条件が満たされると、関数が再帰的に自分自身を呼び出すのを停止するように、少なくとも1つの基本基準または条件が必要です。
Progressive approach −再帰呼び出しは、再帰呼び出しが行われるたびに基本基準に近づくように進行する必要があります。
実装
多くのプログラミング言語は、によって再帰を実装します stacks。一般的に、関数(caller)別の関数を呼び出します(callee)またはそれ自体を呼び出し先として、呼び出し元関数は実行制御を呼び出し先に転送します。この転送プロセスには、発信者から着信者に渡されるデータも含まれる場合があります。
これは、呼び出し元の関数がその実行を一時的に中断し、後で実行制御が呼び出し先の関数から戻ったときに再開する必要があることを意味します。ここで、呼び出し元関数は、それ自体が保留になっている実行ポイントから正確に開始する必要があります。また、作業していたのとまったく同じデータ値が必要です。この目的のために、呼び出し元関数のアクティベーションレコード(またはスタックフレーム)が作成されます。

このアクティベーションレコードは、ローカル変数、仮パラメーター、リターンアドレス、および呼び出し元関数に渡されるすべての情報に関する情報を保持します。
再帰の分析
同じタスクを反復で実行できるため、再帰を使用する理由について議論する人もいるかもしれません。最初の理由は、再帰によってプログラムが読みやすくなり、最新の拡張CPUシステムにより、再帰は反復よりも効率的であるためです。
時間計算量
反復の場合、時間計算量を数えるために反復回数を取ります。同様に、再帰の場合、すべてが一定であると仮定して、再帰呼び出しが行われている回数を把握しようとします。関数への呼び出しはΟ(1)であるため、再帰呼び出しが行われる回数(n)は、再帰関数Ο(n)になります。
スペースの複雑さ
スペースの複雑さは、モジュールの実行に必要な追加スペースの量としてカウントされます。反復の場合、コンパイラーは余分なスペースをほとんど必要としません。コンパイラーは、反復で使用される変数の値を更新し続けます。ただし、再帰の場合、システムは再帰呼び出しが行われるたびにアクティベーションレコードを保存する必要があります。したがって、再帰関数の空間の複雑さは、反復を伴う関数の空間の複雑さよりも高くなる可能性があると考えられます。
ハノイの塔は、3つの塔(ペグ)で構成される数学パズルであり、複数のリングが描かれているとおりです-

これらのリングはサイズが異なり、昇順で積み重ねられます。つまり、小さい方のリングが大きい方のリングの上に配置されます。ディスクの数が増えるパズルの他のバリエーションがありますが、タワーの数は同じままです。
ルール
使命は、配置の順序に違反することなく、すべてのディスクを別のタワーに移動することです。ハノイの塔が従うべきいくつかのルールは次のとおりです。
- タワー間で一度に移動できるディスクは1つだけです。
- 「トップ」ディスクのみを取り外すことができます。
- 大きなディスクを小さなディスクの上に置くことはできません。
以下は、3つのディスクでハノイの塔のパズルを解くアニメーション表現です。

n個のディスクを持つハノイの塔パズルは最小限で解決できます 2n−1ステップ。このプレゼンテーションは、3つのディスクを持つパズルが取ったことを示しています23 - 1 = 7 ステップ。
アルゴリズム
ハノイの塔のアルゴリズムを作成するには、最初に、より少ないディスク数、たとえば→1または2でこの問題を解決する方法を学ぶ必要があります。3つのタワーに名前を付けます。 source、 destination そして aux(ディスクの移動を支援するためのみ)。ディスクが1つしかない場合は、ソースペグからデスティネーションペグに簡単に移動できます。
ディスクが2つある場合-
- まず、小さい方の(上部の)ディスクを補助ペグに移動します。
- 次に、大きい方の(下の)ディスクを宛先ペグに移動します。
- そして最後に、小さい方のディスクをauxから宛先ペグに移動します。

これで、3つ以上のディスクを備えたハノイの塔のアルゴリズムを設計できるようになりました。ディスクのスタックを2つの部分に分割します。最大のディスク(n番目のディスク)は1つの部分にあり、他のすべての(n-1)ディスクは2番目の部分にあります。
私たちの究極の目的は、ディスクを移動することです nソースからデスティネーションへ、そして他のすべての(n1)ディスクをその上に置きます。与えられたすべてのディスクセットに同じものを再帰的に適用することを想像できます。
従う手順は次のとおりです。
Step 1 − Move n-1 disks from source to aux
Step 2 − Move nth disk from source to dest
Step 3 − Move n-1 disks from aux to destハノイの塔の再帰的アルゴリズムは、次のように駆動できます。
START
Procedure Hanoi(disk, source, dest, aux)
IF disk == 1, THEN
move disk from source to dest
ELSE
Hanoi(disk - 1, source, aux, dest) // Step 1
move disk from source to dest // Step 2
Hanoi(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOPCプログラミングでの実装を確認するには、ここをクリックしてください。
フィボナッチ数列は、前の2つの数を加算することによって次の数を生成します。フィボナッチ数列は2つの数字から始まります-F0 & F1。Fの初期値は0&F 1は、それぞれ、0,1または1,1を取ることができます。
フィボナッチ数列は以下の条件を満たす-
Fn = Fn-1 + Fn-2したがって、フィボナッチ数列は次のようになります。
F 8 = 0 1 1 2 3 5 8 13
または、これ-
F 8 = 1 1 2 3 5 8 13 21
例示の目的のために、Fのフィボナッチ8はとして表示されます-

フィボナッチ反復アルゴリズム
まず、フィボナッチ数列の反復アルゴリズムのドラフトを作成します。
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
display f0, f1
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
display fib
end for
end procedure上記のアルゴリズムのCプログラミング言語での実装については、ここをクリックしてください。
フィボナッチ再帰アルゴリズム
再帰的アルゴリズムのフィボナッチ数列を作成する方法を学びましょう。再帰の基本基準。
START
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
display f0, f1
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
display fib
end for
END上記のアルゴリズムのcプログラミング言語での実装を確認するには、ここをクリックしてください。