ヒープデータ構造

ヒープは、バランス二分木データ構造の特殊なケースであり、ルートノードキーがその子と比較され、それに応じて配置されます。場合α 子ノードがあります β 次に−

key（α）≥key（β）

親の値が子の値よりも大きいため、このプロパティは次のように生成します。 Max Heap。この基準に基づいて、ヒープには2つのタイプがあります-

For Input → 35 33 42 10 14 19 27 44 26 31

Min-Heap −ルートノードの値がその子のいずれか以下である場合。

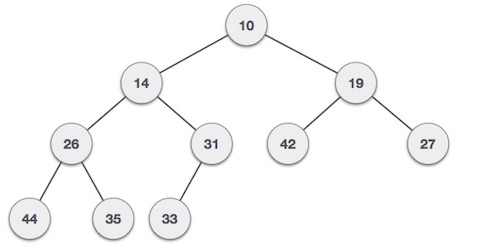
Max-Heap −ルートノードの値がその子のいずれか以上である場合。

両方のツリーは、同じ入力と到着順序を使用して構築されます。

最大ヒープ構築アルゴリズム

同じ例を使用して、最大ヒープがどのように作成されるかを示します。最小ヒープを作成する手順は似ていますが、最大値ではなく最小値を使用します。

一度に1つの要素を挿入することにより、最大ヒープのアルゴリズムを導出します。いつでも、ヒープはそのプロパティを維持する必要があります。挿入中、すでにヒープ化されたツリーにノードを挿入していることも前提としています。

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Note −最小ヒープ構築アルゴリズムでは、親ノードの値が子ノードの値よりも小さいと予想されます。

アニメーションイラストでマックスヒープの構成を理解しましょう。以前に使用したものと同じ入力サンプルを検討します。

最大ヒープ削除アルゴリズム

最大ヒープから削除するアルゴリズムを導出しましょう。最大（または最小）ヒープの削除は、最大（または最小）値を削除するために常にルートで行われます。

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.