物理学-重力
前書き
宇宙で見つかったすべての天体は互いに引き付け合い、これらの天体間の引力は、 gravitational force。

万有引力の法則
宇宙のすべての物体には、それらの質量の積に正比例し、それらの間の距離の2乗に反比例する力で他のすべての物体を引き付ける特性があります(下の画像を参照)。
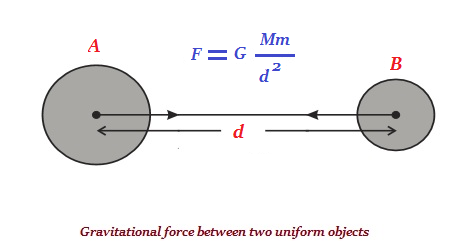
F = 2つのオブジェクト「A」と「B」の間の引力
M =「A」の質量
m =「B」の質量
d2 =「A」と「B」の間の距離の2乗
G =は比例定数であり、万有引力定数として知られています。
GのSI単位は N m2 kg–2。これは、力、距離、および質量の単位を代入することによって得られます(次の式で与えられるように-
$$ G = \ frac {Fd ^ 2} {M \ times m} $$
ヘンリーキャベンディッシュはの値を計算していました ‘G’ なので 6.673 × 10–11 N m2 kg–2。
ヘンリーキャベンディッシュは、敏感なバランスを使用して「G」の値を見つけました。
万有引力の法則の意義
以下は万有引力の顕著な重要性です-
すべての物体(人間を含む)を地球に結合する力を説明します
それは地球の周りの月の動きを説明しています
それは太陽の周りの惑星の動きを説明します
月と太陽による潮汐を明らかにする
フリーフォール
物体が地球に向かって落下するときはいつでも、それは加速を伴います。この加速度は、地球の重力によって発生します。

地球の重力によって発生する加速度は、地球の重力による加速度(または重力による加速度)として知られています。
重力によって発生する加速度は、で表されます。 g。
地球の半径が(極から)赤道に向かって増加するにつれて、 ‘g’ 赤道よりも極で大きくなります。
gの値
gの値は次のように計算されます-
$$ g = G \ frac {M} {R ^ 2} $$
G =普遍的な重力定数、つまり= 6.7 × 10–11 N m2 kg-2
M =地球の質量、つまり= 6 × 1024 kg
R =地球の半径、つまり= 6.4 × 106 m
So,
$$ g = \ frac {6.7 \:\ times 10 ^ {-11} \:Nm ^ 2 \:kg ^ {-2} \:\ times \:6 \:\ times 10 ^ {24} \:kg } {(6.4 \:\ times 10 ^ 6 \:m)^ 2} $$
$ = 9.8 \:m \:s ^ {-2} $
したがって、地球の重力による加速度の値(g)は9.8 ms -2です。