物理学-球面レンズ
前書き
片面または両面が球面である2つの面で結合された透明な材料(通常はガラス)は、「球面レンズ」と呼ばれます。

凸レンズ
レンズは、外側に膨らんだ2つの球面を持っている場合があり(下の画像を参照)、凸レンズまたは二重凸レンズとして知られています。
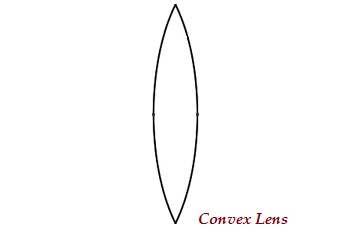
このレンズの中央部分は膨らんでいて(太く)、両端が狭くなっています。
凸レンズは光線を収束させます。したがって、それはとしても知られていますconverging lens。
凹レンズ
レンズは、内側に湾曲した2つの球面を持っている場合があり(下の画像を参照)、凹レンズまたは二重凹レンズとして知られています。
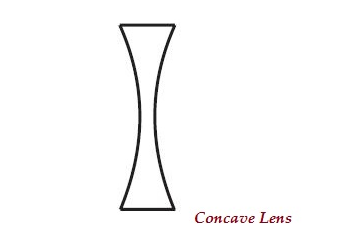
このレンズの中央部分は狭く(内側に湾曲)、両端が厚くなっています。
凹レンズは光線を発散させます。したがって、それはとしても知られていますdiverging lens。
凹面または凸面のレンズには2つの球面があり、これらの各面は球の一部を形成します。これらの球の中心は、centers of curvature、英語の文字で表される 'C。」
曲率の2つの中心があるように、従って、「Cとして表さ1」および「C 2」。
レンズの両方の曲率中心を通る架空の直線は、次のように知られています。 principal axis。
光学中心はレンズの中心点です。'で表されますO。」
口径は、球面レンズの円形の輪郭の実際の直径です。
レンズの主焦点は 'で表されますF。」
レンズは、通常Fとして表される2つの焦点有する1及びF 2。
Focal length主焦点とレンズの光学中心との間の距離です。'で表されますf。」
次の表は、凸レンズによって形成される画像の性質と位置を示しています。
| オブジェクトの位置 | 画像の位置 | 画像のサイズ | 画像の性質 | 画像 |
|---|---|---|---|---|
| 無限大で | 焦点Fで2 | 非常に減少し、指摘された | 実数と反転 |
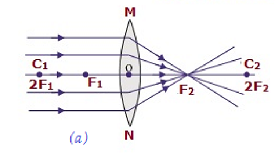
|
| 2Fを超えて1 | B / F W 2及び2F 2 | 減少した | 実数と反転 |
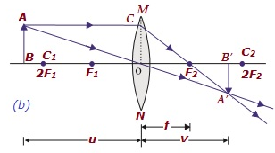
|
| 2Fで1 | 2Fで2 | 同じサイズ | 実数と反転 |
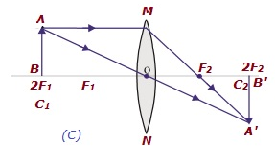
|
| B / w F 1&2F 1 | ビヨンド2F 2 | 拡大 | 実数と反転 |

|
| 焦点Fで1 | 無限大で | 無限大または非常に拡大 | リアル&インバーテッドd |
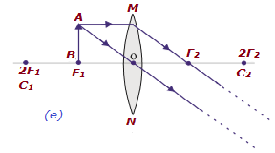
|
| B / W焦点F 1と光学中心O | レンズの対象物と同じ側 | 拡大 | 仮想で直立 |
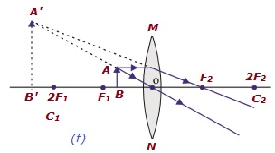
|
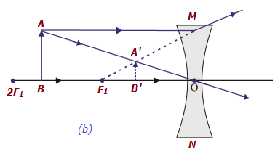
次の表は、凹レンズによって形成された画像の性質と位置を示しています。
| オブジェクトの位置 | 画像の位置 | 画像の相対サイズ | 画像の性質 | 画像 |
|---|---|---|---|---|
| 無限大で | 焦点Fで1 | 非常にディミニシェd、指摘 | 仮想で直立 |
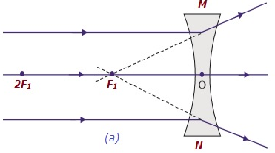
|
| レンズの白黒無限大と光学中心O | B / w F 1&オプティカルセンターO | ディミニシェd | 仮想で直立 |
|
レンズフォーミュラ
式は次のように表されます。
レンズの公式は、物体と距離の関係を表します(つまり、 u)、画像距離(つまり v)、およびレンズの焦点距離(すなわちf)。
$$ \ frac {1} {v}-\ frac {1} {u} = \ frac {1} {f} $$