衛星通信の原理

A satellite と呼ばれる数学的に予測可能な経路で別の物体の周りを移動する物体です Orbit。通信衛星は、インターネットアプリケーションとともに、電気通信、ラジオ、テレビで役立つ宇宙のマイクロ波リピーターステーションに他なりません。

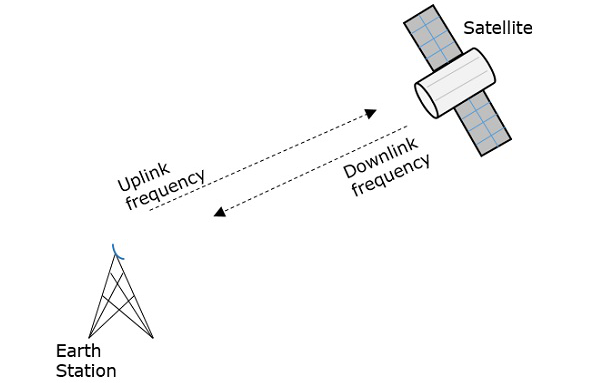
A repeaterは、受信して再送信する信号の強度を高める回路です。しかし、ここではこのリピーターはtransponder、送信信号の周波数帯域を受信信号から変更します。

信号が空間に送られる周波数はと呼ばれます Uplink frequency、トランスポンダによって送信される頻度は Downlink frequency。

次の図は、この概念を明確に示しています。

それでは、衛星通信の長所、短所、およびアプリケーションを見てみましょう。

衛星通信-利点

衛星通信には、次のような多くの利点があります。

Flexibility
新しい回路の設置が簡単
距離は簡単にカバーされ、コストは関係ありません
放送の可能性
地球の隅々まで覆われています
ユーザーはネットワークを制御できます

衛星通信-デメリット

衛星通信には以下の欠点があります-

セグメントや打ち上げなどの初期費用が高すぎる。
周波数の混雑
干渉と伝播

衛星通信-アプリケーション

衛星通信は、次の分野でその用途があります-

ラジオ放送で。
DTHなどのテレビ放送で。
データ転送用のインターネット接続の提供、GPSアプリケーション、インターネットサーフィンなどのインターネットアプリケーション。
音声通信用。
多くの分野で、研究開発部門向け。
軍事用途およびナビゲーション。

軌道上での衛星の向きは、ケプラーの法則と呼ばれる3つの法則に依存します。

ケプラーの法則

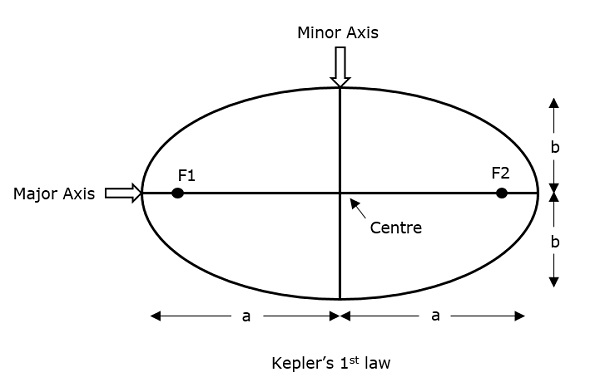
天文学者のヨハネス・ケプラー（1571-1630）は、衛星の動きに関して3つの革命的な法則を与えました。一次衛星（地球）の周りを衛星がたどる経路はellipse。Ellipseには2つの焦点があります-F1 そして F2、地球はそれらの1つです。

オブジェクトの中心から楕円軌道上の点までの距離を考慮すると、中心から楕円の最も遠い点は次のように呼ばれます。 apogee 中心からの楕円の最短点は次のように呼ばれます perigee。

ケプラーの1^番目の法則

ケプラーの第¹法則は、「すべての惑星は、太陽を焦点の1つとして、楕円軌道で太陽の周りを回転する」と述べています。そのため、衛星は地球を焦点の1つとして楕円軌道を移動します。

楕円の半主軸は 'で表されますa'および短半径は次のように表されます b。したがって、このシステムの離心率eは次のように書くことができます。

$$ e = \ frac {\ sqrt {a ^ {2} -b ^ {2}}} {a} $$

Eccentricity (e) −円ではなく、楕円の形状の違いを定義するパラメータです。
Semi-major axis (a) −これは、中心に沿って2つの焦点を結ぶように描かれた最長の直径であり、両方のアポジ（中心から楕円の最も遠い点）に接触します。
Semi-minor axis (b) −両方の境界（中心からの楕円の最短点）に接する、中心を通る最短の直径です。

これらは次の図でよく説明されています。

楕円軌道の場合、離心率は0と1の間にあることが常に望ましいです。つまり、0 <e <1であるため、 e ゼロになると、パスは楕円形ではなくなり、円形パスに変換されます。

ケプラーの2^番目の法則

ケプラーの2^回目「の時間の等間隔のために、衛星がカバーするエリアは、地球の中心に対して等しい。」、法律状態

次の図を見るとわかります。

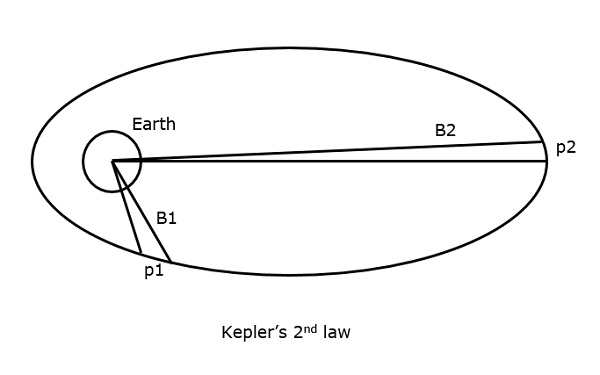
衛星がカバーしていると仮定します p1 そして p2 同じ時間間隔での距離、次に面積 B1 そして B2 それぞれ両方のインスタンスでカバーされ、等しい。

ケプラーの3^番目の法則

ケプラーの3^番目の「軌道の周期的な時間の正方形の2つの物体間の平均距離の3乗に比例している。」、という法則状態

これは数学的に次のように書くことができます

$$ T ^ {2} \：\ alpha \：\：a ^ {3} $$

これは意味します

$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {GM} a ^ {3} $$

ここで、$ \ frac {4 \ pi ^ {2}} {GM} $は比例定数です（ニュートン力学による）

$$ T ^ {2} = \ frac {4 \ pi ^ {2}} {\ mu} a ^ {3} $$

μは、地球の地心重力定数=、すなわちΜ= 3.986005×10 ¹⁴ m個³ /秒²

$$ 1 = \ left（\ frac {2 \ pi} {T} \ right）^ {2} \ frac {a ^ {3}} {\ mu} $$

$$ 1 = n ^ {2} \ frac {a ^ {3}} {\ mu} \：\：\：\ Rightarrow \：\：\：a ^ {3} = \ frac {\ mu} {n ^ {2}} $$

どこ n =ラジアン/秒単位の衛星の平均運動

衛星の軌道機能は、これらのケプラーの法則の助けを借りて計算されます。

これらに加えて、注意しなければならない重要なことがあります。衛星は、地球の周りを回転するときに、重力である地球からの引っ張り力を受けます。また、それは太陽と月からいくらかの引っ張り力を経験します。したがって、それに作用する2つの力があります。彼らは-

Centripetal force −軌道経路を移動する物体をそれ自体に向かって引き寄せる傾向がある力は、次のように呼ばれます。 centripetal force。
Centrifugal force −軌道経路を移動する物体をその位置から遠ざける傾向がある力は、次のように呼ばれます。 centrifugal force。

したがって、衛星は軌道上にとどまるためにこれら2つの力のバランスをとる必要があります。

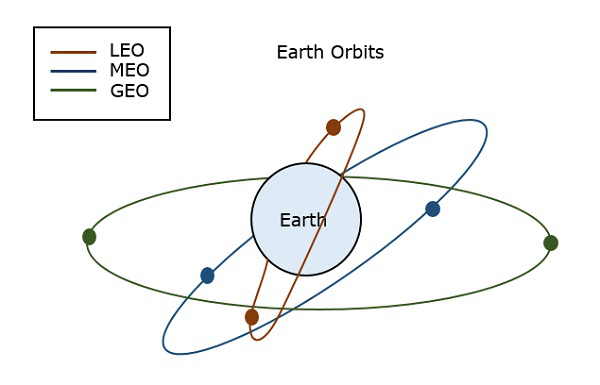
地球軌道

衛星は、宇宙に打ち上げられたときに、その革命のための特定の方法を提供するために特定の軌道に配置する必要があります。これにより、アクセス可能性を維持し、科学、軍事、または商業のいずれの目的にも役立ちます。地球に関して衛星に割り当てられているそのような軌道は、Earth Orbits。これらの軌道にある衛星は地球ですOrbit Satellites。

地球軌道の重要な種類は次のとおりです-

静止地球軌道
中軌道
低軌道

静止地球軌道衛星

A Geo-Synchronous Earth Orbit (GEO)衛星は、地球から22,300マイルの高度に配置されている衛星です。この軌道はと同期していますside real day（つまり、23時間56分）。この軌道はできますhave inclination and eccentricity。円形ではない場合があります。この軌道は、地球の極で傾けることができます。しかし、地球から見ると静止しているように見えます。

同じ静止軌道で、円形で赤道面にある場合は、次のように呼ばれます。 geo-stationary orbit。これらの衛星は、地球の赤道上35,900 km（静止衛星と同じ）に配置され、地球の方向（西から東）に対して回転し続けます。これらの衛星は地球に対して静止していると見なされているため、その名前が示しています。

静止地球軌道衛星は、天気予報、衛星テレビ、衛星ラジオ、その他の種類のグローバル通信に使用されます。

次の図は、静止軌道と静止軌道の違いを示しています。自転軸は地球の動きを示しています。

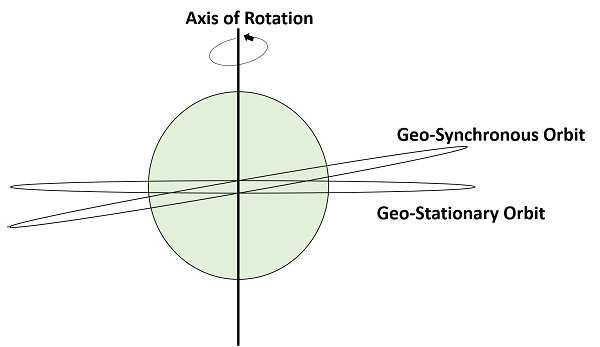
Note−すべての静止軌道は、静止軌道です。しかし、すべての静止軌道は静止軌道ではありません。

中軌道衛星

Medium Earth Orbit (MEO)衛星ネットワークは、地球の表面から約8000マイルの距離を周回します。MEO衛星から送信された信号は、より短い距離を移動します。これは、受信側の信号強度の向上につながります。これは、受信側でより小さく、より軽量な受信端子を使用できることを示しています。

信号は衛星との間の距離が短いため、送信遅延が少なくなります。 Transmission delay 信号が衛星に到達し、受信ステーションに戻るのにかかる時間として定義できます。

リアルタイム通信の場合、伝送遅延が短いほど、通信システムは優れています。例として、GEO衛星が往復に0.25秒を必要とする場合、MEO衛星は同じ旅行を完了するのに0.1秒未満しか必要としません。MEOは、2GHz以上の周波数範囲で動作します。