Pythonデザインパターン-セット
セットは、反復可能、変更可能であり、重複する要素が含まれていない順序付けられていないコレクションとして定義できます。Pythonでは、セットクラスは数学的なセットの表記です。セットを使用する主な利点は、特定の要素をチェックするための高度に最適化された方法が含まれていることです。
Pythonには、フリーズセットと呼ばれる別のカテゴリが含まれています。これらのセットは、必要な結果を生成するメソッドと演算子のみをサポートする不変オブジェクトです。
セットを実装する方法は?
次のプログラムは、セットの実装に役立ちます-
# Set in Python
# Creating two sets
set1 = set()
set2 = set()
# Adding elements to set1
for i in range(1, 6):
set1.add(i)
# Adding elements to set2
for i in range(3, 8):
set2.add(i)
print("Set1 = ", set1)
print("Set2 = ", set2)
print("\n")
# Union of set1 and set2
set3 = set1 | set2# set1.union(set2)
print("Union of Set1 & Set2: Set3 = ", set3)
# Intersection of set1 and set2
set4 = set1 & set2# set1.intersection(set2)
print("Intersection of Set1 & Set2: Set4 = ", set4)
print("\n")
# Checking relation between set3 and set4
if set3 > set4: # set3.issuperset(set4)
print("Set3 is superset of Set4")
elif set3 < set4: # set3.issubset(set4)
print("Set3 is subset of Set4")
else : # set3 == set4
print("Set3 is same as Set4")
# displaying relation between set4 and set3
if set4 < set3: # set4.issubset(set3)
print("Set4 is subset of Set3")
print("\n")
# difference between set3 and set4
set5 = set3 - set4
print("Elements in Set3 and not in Set4: Set5 = ", set5)
print("\n")
# checkv if set4 and set5 are disjoint sets
if set4.isdisjoint(set5):
print("Set4 and Set5 have nothing in common\n")
# Removing all the values of set5
set5.clear()
print("After applying clear on sets Set5: ")
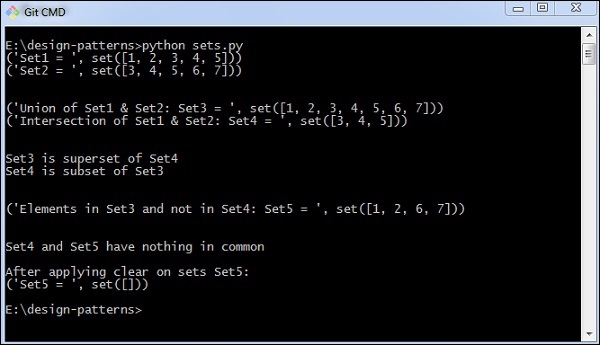
print("Set5 = ", set5)出力
上記のプログラムは次の出力を生成します-
凍結されたセットは、次のプログラムを使用してデモンストレーションできます-
normal_set = set(["a", "b","c"])
# Adding an element to normal set is fine
normal_set.add("d")
print("Normal Set")
print(normal_set)
# A frozen set
frozen_set = frozenset(["e", "f", "g"])
print("Frozen Set")
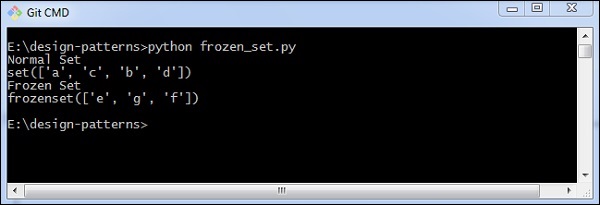
print(frozen_set)出力
上記のプログラムは次の出力を生成します-