TensorFlow-単層パーセプトロン
単層パーセプトロンを理解するには、人工ニューラルネットワーク(ANN)を理解することが重要です。人工ニューラルネットワークは、そのメカニズムが生物学的神経回路の機能に触発された情報処理システムです。人工ニューラルネットワークは、相互に接続された多くの処理ユニットを備えています。以下は、人工ニューラルネットワークの概略図です-
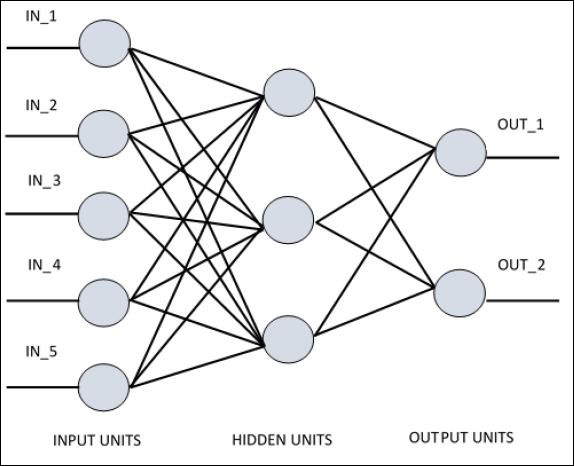
この図は、非表示のユニットが外部レイヤーと通信していることを示しています。一方、入力ユニットと出力ユニットは、ネットワークの隠れ層を介してのみ通信します。
ノードとの接続パターン、レイヤーの総数、入力と出力間のノードのレベル、およびレイヤーごとのニューロンの数によって、ニューラルネットワークのアーキテクチャが定義されます。
アーキテクチャには2つのタイプがあります。これらのタイプは、次のように機能的な人工ニューラルネットワークに焦点を当てています-
- 単層パーセプトロン
- 多層パーセプトロン
単層パーセプトロン
単層パーセプトロンは、最初に提案されたニューラルモデルです。ニューロンのローカルメモリの内容は、重みのベクトルで構成されます。単層パーセプトロンの計算は、それぞれが重みのベクトルの対応する要素で乗算された値を持つ入力ベクトルの合計の計算に対して実行されます。出力に表示される値は、活性化関数の入力になります。

TensorFlowを使用した画像分類問題の単層パーセプトロンの実装に焦点を当てましょう。単層パーセプトロンを説明するための最良の例は、「ロジスティック回帰」の表現によるものです。
ここで、ロジスティック回帰をトレーニングする次の基本的な手順を考えてみましょう。
重みは、トレーニングの開始時にランダムな値で初期化されます。
トレーニングセットの各要素について、エラーは目的の出力と実際の出力の差で計算されます。計算された誤差は、重みを調整するために使用されます。
このプロセスは、トレーニングセット全体で発生したエラーが指定されたしきい値以上になるまで、最大反復回数に達するまで繰り返されます。
ロジスティック回帰を評価するための完全なコードを以下に示します-
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Construct model
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Minimize error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, \ feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))出力
上記のコードは次の出力を生成します-
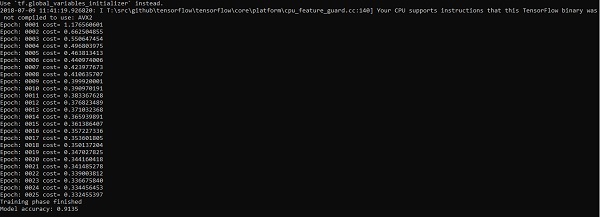
ロジスティック回帰は、予測分析と見なされます。ロジスティック回帰は、データを記述し、1つの従属バイナリ変数と1つ以上の名義変数または独立変数の間の関係を説明するために使用されます。