데이터 구조 및 알고리즘-AVL 트리

이진 검색 트리에 대한 입력이 정렬 된 (오름차순 또는 내림차순) 방식으로 제공되면 어떻게됩니까? 그러면 다음과 같이 보일 것입니다.

BST의 최악의 경우 성능은 선형 검색 알고리즘, 즉 Ο (n)에 가장 가깝습니다. 실시간 데이터에서는 데이터 패턴과 빈도를 예측할 수 없습니다. 따라서 기존 BST의 균형을 맞출 필요가 있습니다.

발명가의 이름을 따서 명명 Adelson, Velski & Landis, AVL trees높이 균형 이진 검색 트리입니다. AVL 트리는 왼쪽 및 오른쪽 하위 트리의 높이를 확인하고 그 차이가 1 이하인지 확인합니다.이 차이를Balance Factor.

여기서 우리는 첫 번째 나무가 균형을 이루고 다음 두 나무가 균형이 맞지 않음을 알 수 있습니다.

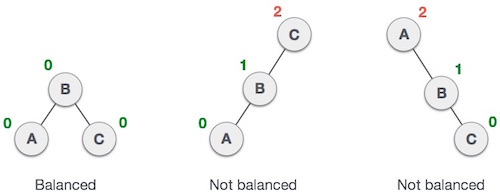
두 번째 트리에서 왼쪽 하위 트리 C 높이가 2이고 오른쪽 하위 트리의 높이가 0이므로 차이는 2입니다. 세 번째 트리에서 오른쪽 하위 트리는 A높이가 2이고 왼쪽이 누락되었으므로 0이고 차이는 다시 2입니다. AVL 트리에서는 차이 (균형 계수)가 1 만 허용됩니다.

BalanceFactor = height(left-sutree) − height(right-sutree)

왼쪽 및 오른쪽 하위 트리의 높이 차이가 1보다 크면 몇 가지 회전 기술을 사용하여 트리가 균형을 이룹니다.

AVL 회전

자체 균형을 유지하기 위해 AVL 트리는 다음 4 가지 종류의 회전을 수행 할 수 있습니다.

• 왼쪽 회전
• 오른쪽 회전
• 왼쪽-오른쪽 회전
• 오른쪽-왼쪽 회전

처음 두 회전은 단일 회전이고 다음 두 회전은 이중 회전입니다. 균형이 맞지 않는 나무를 가지려면 최소한 높이 2의 나무가 필요합니다.이 간단한 나무로 하나씩 이해합시다.

왼쪽 회전

트리가 불균형이되면 노드가 오른쪽 하위 트리의 오른쪽 하위 트리에 삽입되면 단일 왼쪽 회전을 수행합니다.

이 예에서는 node AA의 오른쪽 하위 트리의 오른쪽 하위 트리에 노드가 삽입됨에 따라 불균형이 발생했습니다. 왼쪽 회전은A B의 왼쪽 하위 트리.

오른쪽 회전

왼쪽 하위 트리의 왼쪽 하위 트리에 노드가 삽입되면 AVL 트리가 불균형해질 수 있습니다. 그런 다음 나무는 올바른 회전이 필요합니다.

그림과 같이 불균형 노드는 오른쪽 회전을 수행하여 왼쪽 자식의 오른쪽 자식이됩니다.

왼쪽-오른쪽 회전

이중 회전은 이미 설명 된 회전 버전의 약간 복잡한 버전입니다. 그것들을 더 잘 이해하려면 회전하는 동안 수행되는 각 동작을 기록해야합니다. 먼저 왼쪽-오른쪽 회전을 수행하는 방법을 확인하겠습니다. 왼쪽-오른쪽 회전은 왼쪽 회전과 오른쪽 회전의 조합입니다.

상태	동작
	왼쪽 하위 트리의 오른쪽 하위 트리에 노드가 삽입되었습니다. 이것은 만든다C불균형 노드. 이러한 시나리오로 인해 AVL 트리가 좌우 회전을 수행합니다.
	먼저 왼쪽 하위 트리에서 왼쪽 회전을 수행합니다. C. 이것은 만든다A, 왼쪽 하위 트리 B.
	마디 C 여전히 균형이 맞지 않지만 이제는 왼쪽 하위 트리의 왼쪽 하위 트리 때문입니다.
	이제 나무를 오른쪽으로 회전하여 B 이 서브 트리의 새로운 루트 노드. C 이제 자체 왼쪽 하위 트리의 오른쪽 하위 트리가됩니다.
	이제 나무가 균형을 이룹니다.

오른쪽-왼쪽 회전

두 번째 유형의 이중 회전은 오른쪽-왼쪽 회전입니다. 오른쪽 회전과 왼쪽 회전의 조합입니다.

상태	동작
	오른쪽 하위 트리의 왼쪽 하위 트리에 노드가 삽입되었습니다. 이것은 만든다A, 균형 요소가 2 인 불균형 노드입니다.
	먼저 오른쪽 회전을 수행합니다. C 노드, 만들기 C 자신의 왼쪽 하위 트리의 오른쪽 하위 트리 B. 지금,B 의 오른쪽 하위 트리가됩니다. A.
	마디 A 오른쪽 하위 트리의 오른쪽 하위 트리 때문에 여전히 균형이 맞지 않으며 왼쪽 회전이 필요합니다.
	왼쪽 회전은 B 서브 트리의 새 루트 노드. A 오른쪽 하위 트리의 왼쪽 하위 트리가됩니다. B.
	이제 나무가 균형을 이룹니다.