데이터 구조-분할 및 정복
분할 및 정복 접근 방식에서는 손에 들고있는 문제가 더 작은 하위 문제로 나누어 진 다음 각 문제가 독립적으로 해결됩니다. 하위 문제를 더 작은 하위 문제로 계속 나누면 결국 더 이상 분할이 불가능한 단계에 도달 할 수 있습니다. 이러한 "원자 적"가장 작은 하위 문제 (분수)가 해결됩니다. 모든 하위 문제의 솔루션은 원래 문제의 솔루션을 얻기 위해 최종적으로 병합됩니다.
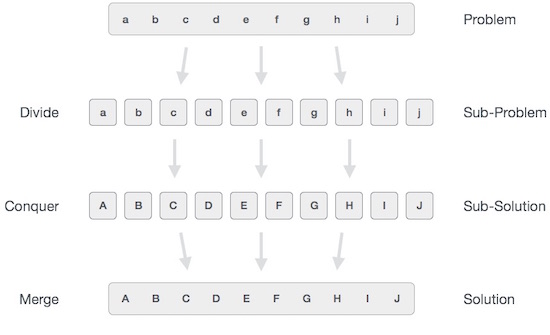
광범위하게 이해할 수 있습니다. divide-and-conquer 3 단계 프로세스로 접근합니다.
나누기 / 끊기
이 단계에는 문제를 더 작은 하위 문제로 나누는 작업이 포함됩니다. 하위 문제는 원래 문제의 일부를 나타내야합니다. 이 단계는 일반적으로 하위 문제가 더 이상 나눌 수 없을 때까지 문제를 나누기 위해 재귀 적 접근 방식을 취합니다. 이 단계에서 하위 문제는 본질적으로 원자가되지만 여전히 실제 문제의 일부를 나타냅니다.
정복 / 해결
이 단계는 해결해야 할 작은 하위 문제를 많이받습니다. 일반적으로이 수준에서 문제는 자체적으로 '해결 된'것으로 간주됩니다.
병합 / 결합
더 작은 하위 문제가 해결되면이 단계는 원래 문제의 솔루션을 공식화 할 때까지 반복적으로 결합합니다. 이 알고리즘 접근 방식은 재귀 적으로 작동하며 정복 및 병합 단계가 너무 가깝게 작동하여 하나로 표시됩니다.
예
다음 컴퓨터 알고리즘은 divide-and-conquer 프로그래밍 방식-
- 병합 정렬
- 빠른 정렬
- 이진 검색
- Strassen의 행렬 곱셈
- 가장 가까운 쌍 (포인트)
컴퓨터 문제를 해결하는 데 사용할 수있는 다양한 방법이 있지만 앞서 언급 한 것은 분할 및 정복 접근 방식의 좋은 예입니다.