힙 데이터 구조
힙은 균형 잡힌 이진 트리 데이터 구조의 특수한 경우로 루트 노드 키가 자식 키와 비교되고 그에 따라 정렬됩니다. 만약α 자식 노드 있음 β 다음-
키 (α) ≥ 키 (β)
parent 값이 child 값보다 크므로이 속성은 Max Heap. 이 기준에 따라 힙은 두 가지 유형이 될 수 있습니다.
For Input → 35 33 42 10 14 19 27 44 26 31Min-Heap − 루트 노드의 값이 자식 중 하나보다 작거나 같은 경우.
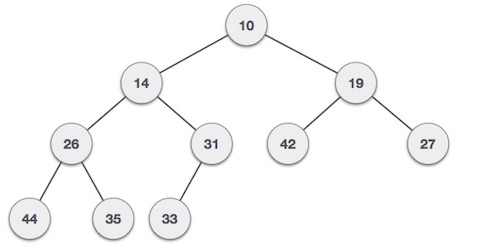
Max-Heap − 루트 노드의 값이 자식 중 하나보다 크거나 같은 경우.

두 트리는 동일한 입력 및 도착 순서를 사용하여 구성됩니다.
최대 힙 구성 알고리즘
동일한 예제를 사용하여 Max Heap이 생성되는 방법을 보여줄 것입니다. 최소 힙을 만드는 절차는 비슷하지만 최대 값 대신 최소 값을 사용합니다.
한 번에 하나의 요소를 삽입하여 최대 힙에 대한 알고리즘을 도출 할 것입니다. 언제든지 힙은 속성을 유지해야합니다. 삽입하는 동안 이미 힙화 된 트리에 노드를 삽입한다고 가정합니다.
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.Note − Min Heap 구성 알고리즘에서 부모 노드의 값이 자식 노드의 값보다 작을 것으로 예상합니다.
애니메이션 일러스트레이션으로 Max Heap 구성을 이해해 봅시다. 이전에 사용한 것과 동일한 입력 샘플을 고려합니다.

최대 힙 삭제 알고리즘
최대 힙에서 삭제할 알고리즘을 유도 해 보겠습니다. 최대 (또는 최소) 힙의 삭제는 항상 루트에서 발생하여 최대 (또는 최소) 값을 제거합니다.
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.