AI - popularne algorytmy wyszukiwania

Wyszukiwanie to uniwersalna technika rozwiązywania problemów w AI. Istnieje kilka gier dla jednego gracza, takich jak gry kaflowe, Sudoku, krzyżówka itp. Algorytmy wyszukiwania pomagają w wyszukiwaniu określonej pozycji w takich grach.

Problemy z odnajdywaniem ścieżki jednego agenta

Gry takie jak 3X3 z ośmioma kafelkami, 4X4 z piętnastoma kafelkami i 5X5 z dwudziestoma czterema kafelkami są wyzwaniami polegającymi na znajdowaniu ścieżki dla jednego agenta. Składają się z matrycy płytek z pustą płytką. Gracz musi ułożyć płytki, przesuwając je pionowo lub poziomo w puste miejsce w celu osiągnięcia jakiegoś celu.

Inne przykłady problemów ze znajdowaniem ścieżki pojedynczego agenta to Problem komiwojażera, Kostka Rubika i Dowodzenie twierdzeń.

Wyszukaj terminologię

Problem Space- To środowisko, w którym odbywa się poszukiwanie. (Zbiór stanów i zestaw operatorów do zmiany tych stanów)
Problem Instance - To jest stan początkowy + stan celu.
Problem Space Graph- Stanowi problem. Stany są wyświetlane przez węzły, a operatory przez krawędzie.
Depth of a problem - Długość najkrótszej ścieżki lub najkrótszej sekwencji operatorów od stanu początkowego do stanu docelowego.
Space Complexity - Maksymalna liczba węzłów przechowywanych w pamięci.
Time Complexity - Maksymalna liczba tworzonych węzłów.
Admissibility - właściwość algorytmu, który zawsze znajduje optymalne rozwiązanie.
Branching Factor - Średnia liczba węzłów potomnych na wykresie przestrzeni problemu.
Depth - Długość najkrótszej ścieżki od stanu początkowego do stanu docelowego.

Strategie wyszukiwania typu Brute-Force

Są najprostsze, ponieważ nie wymagają żadnej wiedzy dziedzinowej. Działają dobrze z niewielką liczbą możliwych stanów.

Wymagania -

Opis stanu
Zestaw prawidłowych operatorów
Stan początkowy
Opis stanu celu

Przeszukiwanie wszerz

Rozpoczyna się od węzła głównego, najpierw bada sąsiednie węzły i przesuwa się w kierunku sąsiadów następnego poziomu. Generuje jedno drzewo na raz, aż do znalezienia rozwiązania. Można to zaimplementować za pomocą struktury danych kolejki FIFO. Ta metoda zapewnia najkrótszą ścieżkę do rozwiązania.

Gdyby branching factor(średnia liczba węzłów potomnych dla danego węzła) = b i głębokość = d, a następnie liczba węzłów na poziomie d = b ^d .

Całkowita liczba węzłów utworzonych w najgorszym przypadku to b + b ² + b ³ +… + b ^d .

Disadvantage- Ponieważ każdy poziom węzłów jest zapisywany w celu utworzenia następnego, zajmuje dużo miejsca w pamięci. Wymagana przestrzeń do przechowywania węzłów jest wykładnicza.

Jego złożoność zależy od liczby węzłów. Może sprawdzić zduplikowane węzły.

Przeszukiwanie w głąb

Jest implementowany rekurencyjnie ze strukturą danych stosu LIFO. Tworzy ten sam zestaw węzłów, co metoda Breadth-First, tylko w innej kolejności.

Ponieważ węzły na pojedynczej ścieżce są przechowywane w każdej iteracji od węzła głównego do węzła-liścia, zapotrzebowanie na miejsce do przechowywania węzłów jest liniowe. Przy współczynniku rozgałęzienia b i głębokości m , przestrzeń magazynowa wynosi bm.

Disadvantage- Ten algorytm nie może kończyć się i działać w nieskończoność na jednej ścieżce. Rozwiązaniem tego problemu jest wybranie głębokości odcięcia. Jeśli idealnym punktem odcięcia jest d , a wybrana wartość odcięcia jest mniejsza niż d , to algorytm może się nie powieść. Jeśli wybrana wartość odcięcia jest większa niż d , to czas wykonania wydłuża się.

Jego złożoność zależy od liczby ścieżek. Nie może sprawdzić zduplikowanych węzłów.

Wyszukiwanie dwukierunkowe

Przeszukuje do przodu od stanu początkowego i wstecz od stanu docelowego, aż oba spotkają się, aby zidentyfikować wspólny stan.

Ścieżka ze stanu początkowego jest łączona z odwrotną ścieżką ze stanu docelowego. Każde wyszukiwanie jest wykonywane tylko do połowy całkowitej ścieżki.

Jednolite wyszukiwanie kosztów

Sortowanie odbywa się w rosnącym koszcie ścieżki do węzła. Zawsze rozwija najmniej kosztowny węzeł. Jest to identyczne z wyszukiwaniem według szerokości, jeśli każde przejście ma ten sam koszt.

Bada ścieżki w kolejności rosnących kosztów.

Disadvantage- Może istnieć wiele długich ścieżek o koszcie ≤ C *. Jednolite wyszukiwanie kosztów musi zbadać je wszystkie.

Iteracyjne pogłębianie wyszukiwania w głąb

Wykonuje przeszukiwanie wgłębne do poziomu 1, rozpoczyna od nowa, wykonuje pełne przeszukiwanie w głąb w pierwszej kolejności do poziomu 2 i kontynuuje w taki sposób, aż zostanie znalezione rozwiązanie.

Nigdy nie tworzy węzła, dopóki nie zostaną wygenerowane wszystkie niższe węzły. Oszczędza tylko stos węzłów. Algorytm kończy się, gdy znajdzie rozwiązanie na głębokości d . Liczba węzłów utworzonych na głębokości d wynosi b ^d, a na głębokości d-1 wynosi b ^d-1.

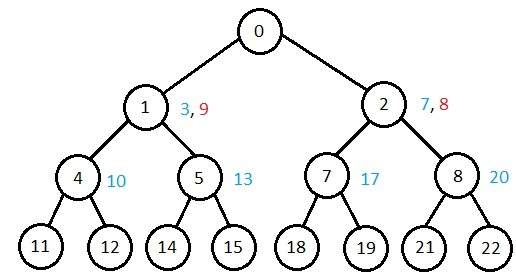
Porównanie różnych złożoności algorytmów

Zobaczmy działanie algorytmów opartych na różnych kryteriach -

Kryterium	Szerokość pierwsza	Najpierw głębokość	Dwukierunkowy	Jednolity koszt	Interaktywne pogłębianie
Czas	b ^d	b ^m	b ^{d / 2}	b ^d	b ^d
Przestrzeń	b ^d	b ^m	b ^{d / 2}	b ^d	b ^d
Optymalność	tak	Nie	tak	tak	tak
Kompletność	tak	Nie	tak	tak	tak

Świadome (heurystyczne) strategie wyszukiwania

Aby rozwiązać duże problemy z dużą liczbą możliwych stanów, należy dodać wiedzę specyficzną dla problemu, aby zwiększyć wydajność algorytmów wyszukiwania.

Funkcje oceny heurystycznej

Obliczają koszt optymalnej ścieżki między dwoma stanami. Funkcja heurystyczna dla gier z przesuwanymi kafelkami jest obliczana poprzez zliczanie liczby ruchów wykonywanych przez każdą płytkę ze stanu celu i dodanie tej liczby ruchów dla wszystkich płytek.

Czyste wyszukiwanie heurystyczne

Rozwija węzły w kolejności ich wartości heurystycznych. Tworzy dwie listy, zamkniętą listę dla już rozwiniętych węzłów i otwartą listę dla utworzonych, ale nierozwiniętych węzłów.

W każdej iteracji węzeł z minimalną wartością heurystyczną jest rozwijany, wszystkie jego węzły potomne są tworzone i umieszczane na zamkniętej liście. Następnie do węzłów potomnych jest stosowana funkcja heurystyczna i są one umieszczane na liście otwartej zgodnie z ich wartością heurystyczną. Krótsze ścieżki są zapisywane, a dłuższe usuwane.

Wyszukiwanie

Jest to najbardziej znana forma wyszukiwania Best First. Unika rozwijania ścieżek, które już są drogie, ale najpierw rozwija najbardziej obiecujące ścieżki.

f (n) = g (n) + h (n), gdzie

g (n) koszt (dotychczas) dotarcia do węzła
h (n) szacowany koszt dotarcia z węzła do celu
f (n) szacunkowy całkowity koszt ścieżki przez n do celu. Jest realizowany przy użyciu kolejki priorytetów poprzez zwiększenie f (n).

Chciwy Najlepsze pierwsze wyszukiwanie

Rozszerza węzeł, który jest szacowany jako najbliższy celu. Rozwija węzły na podstawie f (n) = h (n). Jest realizowany za pomocą kolejki priorytetów.

Disadvantage- Może utknąć w pętli. To nie jest optymalne.

Lokalne algorytmy wyszukiwania

Rozpoczynają od przyszłego rozwiązania, a następnie przechodzą do rozwiązania sąsiedniego. Mogą zwrócić prawidłowe rozwiązanie, nawet jeśli zostanie przerwane w dowolnym momencie przed zakończeniem.

Wyszukiwanie wspinaczkowe

Jest to algorytm iteracyjny, który rozpoczyna się od dowolnego rozwiązania problemu i próbuje znaleźć lepsze rozwiązanie poprzez stopniową zmianę pojedynczego elementu rozwiązania. Jeśli zmiana daje lepsze rozwiązanie, jako nowe rozwiązanie przyjmuje się stopniową zmianę. Ten proces jest powtarzany, dopóki nie będzie żadnych dalszych ulepszeń.

function Hill-Climbing (problem), zwraca stan będący lokalnym maksimum.

inputs: problem, a problem
local variables: current, a node
                 neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
   do neighbor <- a highest_valued successor of current
      if Value[neighbor] ≤ Value[current] then
      return State[current]
      current <- neighbor				  
	
end

Disadvantage - Ten algorytm nie jest ani kompletny, ani optymalny.

Wyszukiwanie wiązki lokalnej

W tym algorytmie przechowuje liczbę stanów w dowolnym momencie. Na początku stany te są generowane losowo. Następcy tych k stanów oblicza się za pomocą funkcji celu. Jeśli którykolwiek z tych następców jest maksymalną wartością funkcji celu, algorytm zatrzymuje się.

W przeciwnym razie (początkowe k stanów ik liczba następców stanów = 2k) stanów umieszcza się w puli. Pula jest następnie sortowana numerycznie. Najwyższe k stanów jest wybieranych jako nowe stany początkowe. Ten proces trwa aż do osiągnięcia maksymalnej wartości.

function BeamSearch ( problem, k ), zwraca stan rozwiązania.

start with k randomly generated states
loop
   generate all successors of all k states
   if any of the states = solution, then return the state
   else select the k best successors
end

Symulowanego wyżarzania

Wyżarzanie to proces ogrzewania i chłodzenia metalu w celu zmiany jego wewnętrznej struktury i modyfikacji jego właściwości fizycznych. Gdy metal stygnie, jego nowa struktura zostaje zatarta, a metal zachowuje nowo uzyskane właściwości. W symulowanym procesie wyżarzania utrzymuje się zmienną temperaturę.

Początkowo ustawiamy wysoką temperaturę, a następnie pozwalamy jej powoli „ostygnąć” w miarę postępów algorytmu. Przy wysokiej temperaturze algorytm dopuszcza gorsze rozwiązania o wysokiej częstotliwości.

Początek

Inicjalizuj k = 0; L = całkowita liczba zmiennych;
Z i → j, wyszukaj różnicę wydajności Δ.
Jeśli Δ <= 0 to zaakceptuj else if exp (-Δ / T (k))> random (0,1) to zaakceptuj;
Powtórz kroki 1 i 2 dla kroków L (k).
k = k + 1;

Powtarzaj kroki od 1 do 4, aż kryteria zostaną spełnione.

Koniec

Problem komiwojażera

W tym algorytmie celem jest znalezienie taniej wycieczki rozpoczynającej się w mieście, odwiedzającej wszystkie miasta na trasie dokładnie raz i kończącej się w tym samym mieście początkowym.

Start
   Find out all (n -1)! Possible solutions, where n is the total number of cities.
   Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
   Finally, keep the one with the minimum cost.
end