Montaż - wprowadzenie
Co to jest język asemblera?
Każdy komputer osobisty jest wyposażony w mikroprocesor, który zarządza działaniami arytmetycznymi, logicznymi i kontrolnymi komputera.
Każda rodzina procesorów ma własny zestaw instrukcji do obsługi różnych operacji, takich jak pobieranie danych wejściowych z klawiatury, wyświetlanie informacji na ekranie i wykonywanie różnych innych zadań. Ten zestaw instrukcji nazywany jest „instrukcjami języka maszynowego”.
Procesor rozumie tylko instrukcje języka maszynowego, które są ciągami jedynek i zer. Jednak język maszynowy jest zbyt niejasny i skomplikowany, aby można go było używać w tworzeniu oprogramowania. Tak więc język asemblera niskiego poziomu jest przeznaczony dla określonej rodziny procesorów, które reprezentują różne instrukcje w kodzie symbolicznym i bardziej zrozumiałej formie.
Zalety języka asemblera
Zrozumienie języka asemblera uświadamia -
- Jak programy współpracują z systemem operacyjnym, procesorem i systemem BIOS;
- Sposób reprezentacji danych w pamięci i innych urządzeniach zewnętrznych;
- Jak procesor uzyskuje dostęp i wykonuje instrukcje;
- Jak instrukcje uzyskują dostęp do danych i je przetwarzają;
- W jaki sposób program uzyskuje dostęp do urządzeń zewnętrznych.
Inne zalety używania języka asemblera to -
Wymaga mniej pamięci i czasu wykonywania;
Pozwala w łatwiejszy sposób na złożone zadania specyficzne dla sprzętu;
Nadaje się do prac, w których liczy się czas;
Jest najbardziej odpowiedni do pisania procedur obsługi przerwań i innych programów rezydujących w pamięci.
Podstawowe cechy sprzętu komputerowego
Główny sprzęt wewnętrzny komputera PC składa się z procesora, pamięci i rejestrów. Rejestry to komponenty procesora, które przechowują dane i adresy. W celu wykonania programu system kopiuje go z urządzenia zewnętrznego do pamięci wewnętrznej. Procesor wykonuje instrukcje programu.
Podstawową jednostką pamięci komputera jest trochę; może być ON (1) lub OFF (0), a grupa 8 powiązanych bitów tworzy bajt na większości nowoczesnych komputerów.
Tak więc bit parzystości jest używany, aby liczba bitów w bajcie była nieparzysta. Jeśli parzystość jest równa, system zakłada, że wystąpił błąd parzystości (choć rzadki), który mógł być spowodowany usterką sprzętową lub zakłóceniem elektrycznym.
Procesor obsługuje następujące rozmiary danych -
- Słowo: 2-bajtowa pozycja danych
- Podwójne słowo: 4-bajtowa (32-bitowa) pozycja danych
- Quadword: 8-bajtowy (64-bitowy) element danych
- Akapit: obszar 16-bajtowy (128-bitowy)
- Kilobajt: 1024 bajty
- Megabajt: 1048576 bajtów
System liczb binarnych
Każdy system liczbowy używa notacji pozycyjnej, tj. Każda pozycja, w której zapisana jest cyfra, ma inną wartość pozycyjną. Każda pozycja jest potęgą podstawy, która wynosi 2 dla systemu liczb binarnych, a te potęgi zaczynają się od 0 i rosną o 1.
W poniższej tabeli przedstawiono wartości pozycyjne 8-bitowej liczby binarnej, w której wszystkie bity są ustawione na ON.
| Wartość bitowa | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|
| Wartość pozycji jako potęga podstawy 2 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Numer bitu | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Wartość liczby binarnej opiera się na obecności 1 bitów i ich wartości pozycyjnej. Zatem wartość danej liczby binarnej to -
1 + 2 + 4 + 8 +16 + 32 + 64 + 128 = 255
czyli to samo co 2 8 - 1.
System liczb szesnastkowych
System liczb szesnastkowych używa podstawy 16. Cyfry w tym systemie mieszczą się w zakresie od 0 do 15. Zgodnie z konwencją, litery od A do F są używane do reprezentowania cyfr szesnastkowych odpowiadających wartościom dziesiętnym od 10 do 15.
Liczby szesnastkowe w obliczeniach służą do skrócenia długich reprezentacji binarnych. Zasadniczo szesnastkowy system liczbowy przedstawia dane binarne, dzieląc każdy bajt na pół i wyrażając wartość każdego pół-bajtu. Poniższa tabela zawiera odpowiedniki dziesiętne, dwójkowe i szesnastkowe -
| Liczba dziesiętna | Reprezentacja binarna | Reprezentacja szesnastkowa |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | ZA |
| 11 | 1011 | b |
| 12 | 1100 | do |
| 13 | 1101 | re |
| 14 | 1110 | mi |
| 15 | 1111 | fa |
Aby przekonwertować liczbę dwójkową na jej szesnastkowy odpowiednik, podziel ją na grupy po 4 kolejne grupy każda, zaczynając od prawej strony, i zapisz te grupy na odpowiednich cyfrach liczby szesnastkowej.
Example - Liczba binarna 1000 1100 1101 0001 jest odpowiednikiem liczby szesnastkowej - 8CD1
Aby przekonwertować liczbę szesnastkową na dwójkową, po prostu zapisz każdą cyfrę szesnastkową na jej 4-cyfrowy odpowiednik binarny.
Example - Liczba szesnastkowa FAD8 jest odpowiednikiem liczby dwójkowej - 1111 1010 1101 1000
Arytmetyka binarna
Poniższa tabela przedstawia cztery proste zasady dodawania binarnego -
| (ja) | (ii) | (iii) | (iv) |
|---|---|---|---|
| 1 | |||
| 0 | 1 | 1 | 1 |
| +0 | +0 | +1 | +1 |
| = 0 | = 1 | = 10 | = 11 |
Reguły (iii) i (iv) pokazują przeniesienie 1-bitu na następną lewą pozycję.
Example
| Dziesiętny | Dwójkowy |
|---|---|
| 60 | 00111100 |
| +42 | 00101010 |
| 102 | 01100110 |
Ujemna wartość binarna jest wyrażana w two's complement notation. Zgodnie z tą zasadą konwersja liczby binarnej na jej wartość ujemną polega na odwróceniu jej wartości bitowych i dodaniu 1 .
Example
| Numer 53 | 00110101 |
| Odwróć bity | 11001010 |
| Dodaj 1 | 0000000 1 |
| Numer -53 | 11001011 |
Aby odjąć jedną wartość od drugiej, przekonwertuj odejmowaną liczbę do formatu uzupełnienia do dwóch i dodaj liczby .
Example
Odejmij 42 od 53
| Numer 53 | 00110101 |
| Numer 42 | 00101010 |
| Odwróć bity 42 | 11010101 |
| Dodaj 1 | 0000000 1 |
| Numer -42 | 11010110 |
| 53 - 42 = 11 | 00001011 |
Przepełnienie ostatniego 1 bitu jest tracone.
Adresowanie danych w pamięci
Proces, za pomocą którego procesor steruje wykonywaniem instrukcji, nazywany jest fetch-decode-execute cycle albo execution cycle. Składa się z trzech ciągłych kroków -
- Pobieranie instrukcji z pamięci
- Dekodowanie lub identyfikacja instrukcji
- Wykonanie instrukcji
Procesor może mieć jednocześnie dostęp do jednego lub większej liczby bajtów pamięci. Rozważmy liczbę szesnastkową 0725H. Ta liczba będzie wymagać dwóch bajtów pamięci. Najstarszy bajt lub najbardziej znaczący bajt to 07, a najmniejszy bajt to 25.
Procesor przechowuje dane w odwrotnej kolejności bajtów, tj. Bajt niskiego rzędu jest przechowywany w niskim adresie pamięci, a bajt wyższego rzędu w adresie dużej pamięci. Tak więc, jeśli procesor przeniesie wartość 0725H z rejestru do pamięci, najpierw prześle 25 do niższego adresu pamięci, a 07 do następnego adresu pamięci.
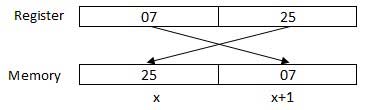
x: adres pamięci
Kiedy procesor pobiera dane numeryczne z pamięci do rejestracji, ponownie odwraca bajty. Istnieją dwa rodzaje adresów pamięci -
Adres bezwzględny - bezpośrednie odniesienie do określonej lokalizacji.
Adres segmentu (lub offset) - adres początkowy segmentu pamięci z wartością offsetu.