Struktury danych i algorytmy - tablice

Tablica to kontener, który może pomieścić ustaloną liczbę elementów, które powinny być tego samego typu. Większość struktur danych wykorzystuje tablice do implementacji swoich algorytmów. Poniżej znajdują się ważne terminy, aby zrozumieć koncepcję Array.

Element - Każdy element przechowywany w tablicy nazywany jest elementem.
Index - Każda lokalizacja elementu w tablicy ma indeks numeryczny, który służy do identyfikacji elementu.

Reprezentacja tablicy

Tablice można deklarować na różne sposoby w różnych językach. Na przykład weźmy deklarację tablicy C.

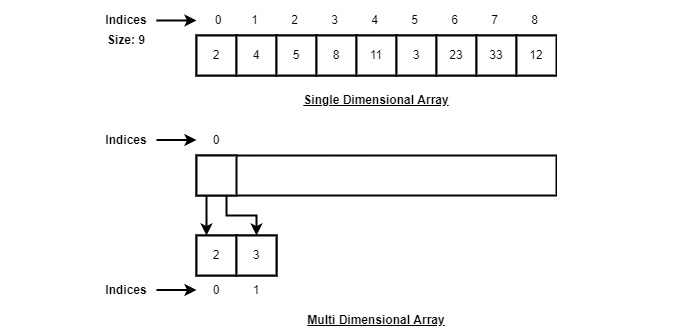
Zgodnie z powyższą ilustracją, należy wziąć pod uwagę następujące ważne kwestie.

Indeks zaczyna się od 0.
Długość tablicy wynosi 10, co oznacza, że może pomieścić 10 elementów.
Dostęp do każdego elementu można uzyskać poprzez jego indeks. Na przykład możemy pobrać element o indeksie 6 jako 9.

Podstawowe operacje

Poniżej przedstawiono podstawowe operacje obsługiwane przez tablicę.

Traverse - wypisuje wszystkie elementy tablicy jeden po drugim.
Insertion - dodaje element pod podanym indeksem.
Deletion - usuwa element pod podanym indeksem.
Search - Przeszukuje element przy użyciu podanego indeksu lub wartości.
Update - Aktualizuje element w podanym indeksie.

W języku C, gdy tablica jest inicjalizowana z rozmiarem, przypisuje wartości domyślne do swoich elementów w następującej kolejności.

Typ danych	Domyślna wartość
bool	fałszywy
zwęglać	0
int	0
pływak	0.0
podwójnie	0.0f
unieważnić
wchar_t	0

Operacja trawersu

Ta operacja polega na przechodzeniu przez elementy tablicy.

Przykład

Następujący program przechodzi i wyświetla elementy tablicy:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Kiedy kompilujemy i wykonujemy powyższy program, daje on następujący wynik -

Wynik

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Operacja wstawiania

Operacja wstawiania polega na wstawieniu jednego lub więcej elementów danych do tablicy. W zależności od wymagań można dodać nowy element na początku, na końcu lub w dowolnym indeksie tablicy.

Tutaj widzimy praktyczną implementację operacji wstawiania, w której dodajemy dane na końcu tablicy -

Przykład

Poniżej przedstawiono implementację powyższego algorytmu -

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Kiedy kompilujemy i wykonujemy powyższy program, daje on następujący wynik -

Wynik

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Aby zobaczyć inne warianty operacji wstawiania tablicy, kliknij tutaj

Operacja usunięcia

Usunięcie oznacza usunięcie istniejącego elementu z tablicy i reorganizację wszystkich elementów tablicy.

Algorytm

Rozważać LA jest tablicą liniową zawierającą N elementy i K jest dodatnią liczbą całkowitą, taką że K<=N. Poniżej znajduje się algorytm usuwania elementu dostępnego na K- ^tej pozycji LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Przykład

Poniżej przedstawiono implementację powyższego algorytmu -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Kiedy kompilujemy i wykonujemy powyższy program, daje on następujący wynik -

Wynik

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Operacja wyszukiwania

Możesz przeprowadzić wyszukiwanie elementu tablicy na podstawie jego wartości lub indeksu.

Algorytm

Rozważać LA jest tablicą liniową zawierającą N elementy i K jest dodatnią liczbą całkowitą, taką że K<=N. Poniżej znajduje się algorytm znajdowania elementu o wartości ITEM przy użyciu wyszukiwania sekwencyjnego.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Przykład

Poniżej przedstawiono implementację powyższego algorytmu -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Kiedy kompilujemy i wykonujemy powyższy program, daje on następujący wynik -

Wynik

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Operacja aktualizacji

Operacja Update odnosi się do aktualizacji istniejącego elementu z tablicy o podanym indeksie.

Algorytm

Rozważać LA jest tablicą liniową zawierającą N elementy i K jest dodatnią liczbą całkowitą, taką że K<=N. Poniżej znajduje się algorytm aktualizacji elementu dostępnego na K- ^tej pozycji LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Przykład

Poniżej przedstawiono implementację powyższego algorytmu -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Kiedy kompilujemy i wykonujemy powyższy program, daje on następujący wynik -

Wynik

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8