Struktury danych - analiza asymptotyczna

Asymptotyczna analiza algorytmu odnosi się do określenia matematycznego ograniczenia / ramkowania jego wydajności w czasie wykonywania. Korzystając z analizy asymptotycznej, możemy bardzo dobrze wywnioskować najlepszy, średni i najgorszy scenariusz algorytmu.

Analiza asymptotyczna jest ograniczona wejściami, tj. Jeśli nie ma danych wejściowych do algorytmu, dochodzi do wniosku, że działa w stałym czasie. Oprócz „danych wejściowych” wszystkie inne czynniki są uważane za stałe.

Analiza asymptotyczna odnosi się do obliczania czasu wykonywania dowolnej operacji w matematycznych jednostkach obliczeniowych. Na przykład czas wykonywania jednej operacji jest obliczany jako f (n), a dla innej operacji może być obliczany jako g (n ² ). Oznacza to, że czas pracy pierwszej operacji będzie wydłużał się liniowo wraz ze wzrostemn a czas wykonywania drugiej operacji wzrośnie wykładniczo, kiedy nwzrasta. Podobnie czas wykonywania obu operacji będzie prawie taki sam, jeślin jest znacznie mały.

Zwykle czas wymagany przez algorytm dzieli się na trzy typy -

Best Case - Minimalny czas potrzebny do wykonania programu.
Average Case - Średni czas potrzebny do wykonania programu.
Worst Case - Maksymalny czas wymagany do wykonania programu.

Notacje asymptotyczne

Poniżej przedstawiono powszechnie używane notacje asymptotyczne do obliczania złożoności algorytmu w czasie.

Ο Notacja
Notacja Ω
θ Notacja

Notacja Big Oh, Ο

Notacja Ο (n) jest formalnym sposobem wyrażenia górnej granicy czasu działania algorytmu. Mierzy najgorszy przypadek złożoności czasowej lub najdłuższy czas, jaki może zająć algorytm.

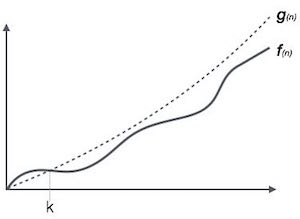
Na przykład dla funkcji f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

Notacja Omega, Ω

Notacja Ω (n) jest formalnym sposobem wyrażenia dolnej granicy czasu działania algorytmu. Mierzy najlepszą złożoność czasową sprawy lub najlepszy czas, jaki może zająć algorytm.

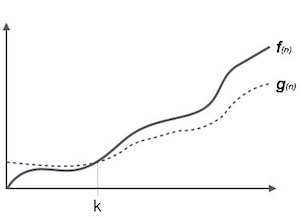
Na przykład dla funkcji f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

Notacja Theta, θ

Notacja θ (n) jest formalnym sposobem wyrażenia zarówno dolnej, jak i górnej granicy czasu działania algorytmu. Jest przedstawiony w następujący sposób -

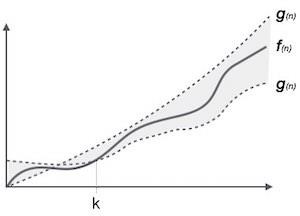
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

Typowe notacje asymptotyczne

Poniżej znajduje się lista niektórych typowych notacji asymptotycznych -

stały	-	Ο (1)
logarytmiczny	-	Ο (log n)
liniowy	-	Ο (n)
n log n	-	Ο (n log n)
kwadratowy	-	Ο (nr ² )
sześcienny	-	Ο (nr ³ )
wielomian	-	n ^{Ο (1)}
wykładniczy	-	2 ^{Ο (n)}