Struktury danych sterty
Sterta to szczególny przypadek zbalansowanej struktury danych drzewa binarnego, w którym klucz węzła głównego jest porównywany z jego potomkami i odpowiednio układany. Jeśliα ma węzeł podrzędny β wtedy -
klucz (α) ≥ klucz (β)
Ponieważ wartość rodzica jest większa niż wartość potomka, ta właściwość generuje Max Heap. W oparciu o te kryteria sterta może mieć dwa typy -
For Input → 35 33 42 10 14 19 27 44 26 31Min-Heap - Gdzie wartość węzła głównego jest mniejsza lub równa którejkolwiek z jego dzieci.
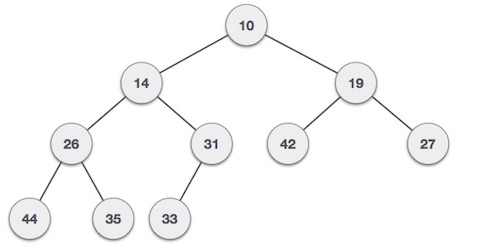
Max-Heap - Gdzie wartość węzła głównego jest większa lub równa którejkolwiek z jego dzieci.

Oba drzewa są konstruowane przy użyciu tego samego wejścia i kolejności przybycia.
Algorytm konstrukcji maksymalnego sterty
Posłużymy się tym samym przykładem, aby zademonstrować, jak powstaje Max Heap. Procedura tworzenia Min Heap jest podobna, ale używamy wartości minimalnych zamiast maksymalnych.
Mamy zamiar wyprowadzić algorytm dla maksymalnego sterty, wstawiając jeden element na raz. W dowolnym momencie sterta musi zachować swoją własność. Podczas wstawiania zakładamy również, że wstawiamy węzeł w już skompresowanym drzewie.
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.Note - W algorytmie konstrukcji Min Heap oczekujemy, że wartość węzła nadrzędnego będzie mniejsza niż wartość węzła podrzędnego.
Zrozummy konstrukcję Max Heap dzięki animowanej ilustracji. Rozważamy tę samą próbkę wejściową, której używaliśmy wcześniej.

Algorytm usuwania maksymalnego sterty
Wyprowadźmy algorytm usuwania z maksymalnego sterty. Usunięcie w Max (lub Min) Sterta zawsze ma miejsce w katalogu głównym w celu usunięcia wartości maksymalnej (lub minimalnej).
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.