Inżynieria mikrofalowa - koszulka H-Plane
Połączenie trójnikowe w płaszczyźnie H jest tworzone przez dołączenie prostego falowodu do prostokątnego falowodu, który ma już dwa porty. Ramiona falowodów prostokątnych tworzą dwa porty tzwcollinear ports tj. Port1 i Port2, podczas gdy nowy Port3 nazywa się uzbrojeniem bocznym lub H-arm. Ta koszulka w kształcie litery H jest również nazywana jakoShunt Tee.
Ponieważ oś ramienia bocznego jest równoległa do pola magnetycznego, to połączenie nazywa się skrzyżowaniem w płaszczyźnie H. Nazywa się to również jakoCurrent junction, gdy pole magnetyczne dzieli się na ramiona. Szczegóły przekroju trójnika w płaszczyźnie H można zrozumieć na poniższym rysunku.

Poniższy rysunek przedstawia połączenie wykonane przez ramię boczne z dwukierunkowym falowodem w celu utworzenia portu szeregowego.
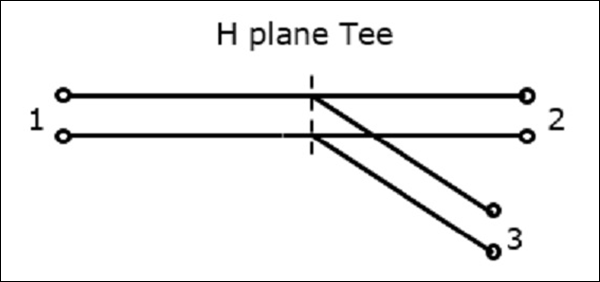
Właściwości koszulki H-Plane
Właściwości trójnika H-Plane Tee można zdefiniować za pomocą jej macierzy $ \ left [S \ right] _ {3 \ times 3} $.
Jest to macierz 3 × 3, ponieważ są 3 możliwe wejścia i 3 możliwe wyjścia.
$ [S] = \ begin {bmatrix} S_ {11} i S_ {12} i S_ {13} \\ S_ {21} i S_ {22} i S_ {23} \\ S_ {31} i S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
Współczynniki rozpraszania $ S_ {13} $ i $ S_ {23} $ są tutaj równe, ponieważ skrzyżowanie jest symetryczne w płaszczyźnie.
Z własności symetrycznej
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} = S_ {13} \: \: S_ {13} = S_ {31} $
Port jest idealnie dopasowany
$ S_ {33} = 0 $
Teraz macierz $ [S] $ można zapisać jako,
$ [S] = \ begin {bmatrix} S_ {11} i S_ {12} i S_ {13} \\ S_ {12} i S_ {22} i S_ {13} \\ S_ {13} i S_ {13 } & 0 \ end {bmatrix} $ ........ Equation 2
Możemy powiedzieć, że mamy cztery niewiadome, biorąc pod uwagę własność symetrii.
Z własności Unitary
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} i S_ {12} i S_ {13} \\ S_ {12} i S_ {22} i S_ {13} \\ S_ {13} i S_ {13} i 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} i S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Mnożąc otrzymujemy
(Zapisując R jako wiersz, a C jako kolumnę)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $........ Equation 3
$ R_2C_2: \ left | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 4
$ R_3C_3: \ left | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 5
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 0 $ ......... Equation 6
Pozostało 2 $ | S_ {13} \ right | ^ 2 = 1 \ quad lub \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 7
$ \ left | S_ {11} \ right | ^ 2 = \ left | S_ {22} \ right | ^ 2 $
$ S_ {11} = S_ {22} $ ......... Equation 8
Z równania 6, $ S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0 $
Ponieważ $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: lub \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
Lub $ S_ {11} = -S_ {12} \: \: lub \: \: S_ {12} = -S_ {11} $......... Equation 9
Używając ich w równaniu 3,
Ponieważ $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: lub \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad lub \ quad 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad lub \ quad S_ {11} = \ frac {1} {2} $..... Equation 10
Z równania 8 i 9,
$ S_ {12} = - \ frac {1} {2} $......... Equation 11
$ S_ {22} = \ frac {1} {2} $......... Equation 12
Zastępując $ S_ {13} $, $ S_ {11} $, $ S_ {12} $ i $ S_ {22} $ z równania 7 i 10, 11 i 12 w równaniu 2,
Otrzymujemy,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
Wiemy, że $ [b] $ = $ [s] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
To jest macierz rozpraszania trójnika w płaszczyźnie H, która wyjaśnia jej właściwości rozpraszania.