Potęga 10: ujemny wykładnik

W tej lekcji zajmiemy się problemami związanymi z wyrażeniami, dla których podstawą jest 10 i które mają ujemne wykładniki.

Rules to find the negative exponent of 10

Załóżmy, że mamy wyrażenie mające 10 ^-n .

• W normalnym trybie wartość 10 ^-n jest wyznaczana przez pomnożenie podstawy
  10 'n' razy w mianowniku i wstawienie 1 do licznika.

• Do rozwiązania tego problemu używamy skrótu. Patrzymy na wykładnik, a następnie piszemy kropkę dziesiętną, po której następuje tyle zer o jeden mniej niż wykładnik i 1.

Oceń ^10-3

Rozwiązanie

Step 1:

Tutaj mamy wyrażenie obejmujące potęgę dziesiątki z wykładnikiem ujemnym.

Podstawa to 10, a wykładnik to -3.

Step 2:

W normalnym trybie wartość ^10-3 można znaleźć, mnożąc podstawę 10 trzy razy w mianowniku i umieszczając 1 w liczniku.

10 ^-3 =

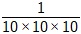
Step 3:

Używając skrótu, stwierdzamy, że wykładnikiem jest -3. Piszemy kropkę dziesiętną, po której następują dwa (o 1 mniej niż 3) zera i 1.

Czyli ^10-3 = 0,001

Oceń ^10-5

Rozwiązanie

Step 1:

Tutaj mamy wyrażenie obejmujące potęgę dziesiątki z wykładnikiem ujemnym.

Podstawa to 10, a wykładnik to -5.

Step 2:

W normalnym trybie wartość ^10–5 uzyskuje się, mnożąc podstawę 10 w mianowniku pięć razy i umieszczając 1 w liczniku.

10 ^-5 =

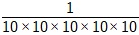
Step 3:

Używając skrótu, znajdujemy wykładnik -5. Piszemy kropkę dziesiętną, po której następują cztery (o 1 mniej niż 5) zera i 1.

Czyli ^10-5 = 0,00001