Algorytm wykresu
Graf to abstrakcyjna notacja używana do reprezentowania połączenia między parami obiektów. Wykres składa się z -
Vertices- Połączone obiekty na wykresie nazywane są wierzchołkami. Wierzchołki są również znane jakonodes.
Edges - Krawędzie to łącza łączące wierzchołki.
Istnieją dwa rodzaje wykresów -
Directed graph - Na wykresie skierowanym krawędzie mają kierunek, tj. Krawędzie przechodzą od jednego wierzchołka do drugiego.
Undirected graph - Na wykresie nieukierunkowanym krawędzie nie mają kierunku.
Kolorowanie wykresu
Kolorowanie wykresu to metoda przypisywania kolorów do wierzchołków wykresu, tak aby żadne dwa sąsiednie wierzchołki nie miały tego samego koloru. Niektóre problemy z kolorowaniem wykresów to:
Vertex coloring - Sposób kolorowania wierzchołków wykresu, tak aby żadne dwa sąsiednie wierzchołki nie miały tego samego koloru.
Edge Coloring - Jest to metoda przypisywania koloru każdej krawędzi, tak aby żadne dwie sąsiednie krawędzie nie miały tego samego koloru.
Face coloring - Przypisuje kolor do każdej ściany lub regionu planarnego wykresu, tak że żadne dwie ściany, które mają wspólną granicę, nie mają tego samego koloru.
Liczba chromatyczna
Liczba chromatyczna to minimalna liczba kolorów wymagana do pokolorowania wykresu. Na przykład liczba chromatyczna poniższego wykresu wynosi 3.

Koncepcję kolorowania grafów stosuje się przy opracowywaniu rozkładów jazdy, przydzielaniu częstotliwości radiowych, Suduku, alokacji rejestrów i kolorowaniu map.
Kroki do kolorowania wykresów
Ustaw wartość początkową każdego procesora w tablicy n-wymiarowej na 1.
Teraz, aby przypisać określony kolor do wierzchołka, określ, czy ten kolor jest już przypisany do sąsiednich wierzchołków, czy nie.
Jeśli procesor wykryje ten sam kolor w sąsiednich wierzchołkach, ustawia jego wartość w tablicy na 0.
Po wykonaniu n 2 porównań, jeśli którykolwiek element tablicy ma wartość 1, to jest to poprawne kolorowanie.
Pseudokod do kolorowania grafów
begin
create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
status[i0,..in-1] = 1
for j varies from 0 to n-1 do
begin
for k varies from 0 to n-1 do
begin
if aj,k=1 and ij=ikthen
status[i0,..in-1] =0
end
end
ok = ΣStatus
if ok > 0, then display valid coloring exists
else
display invalid coloring
endMinimalne drzewo opinające
Drzewo rozpinające, którego suma masy (lub długości) wszystkich jego krawędzi jest mniejsza niż wszystkich innych możliwych drzew rozpinających wykresu G, jest znane jako minimal spanning tree lub minimum cost spanningdrzewo. Poniższy rysunek przedstawia ważony połączony wykres.

Poniżej przedstawiono niektóre możliwe drzewa opinające z powyższego wykresu -



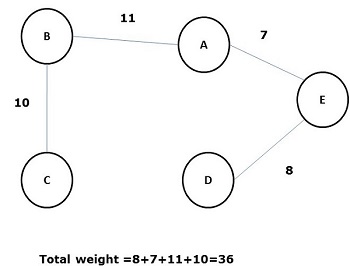



Spośród wszystkich powyższych drzew rozpinających rysunek (d) jest minimalnym drzewem rozpinającym. Koncepcja drzewa rozpinania minimalnych kosztów jest stosowana w problemie komiwojażera, projektowaniu układów elektronicznych, projektowaniu wydajnych sieci i projektowaniu wydajnych algorytmów routingu.
Aby wdrożyć drzewo obejmujące minimalne koszty, stosuje się dwie następujące metody:
- Algorytm Prima
- Algorytm Kruskala
Algorytm Prima
Algorytm Prima to zachłanny algorytm, który pomaga nam znaleźć minimalne drzewo rozpinające dla ważonego grafu niekierowanego. Najpierw wybiera wierzchołek i znajduje krawędź o najmniejszym ciężarze na tym wierzchołku.
Kroki algorytmu Prim
Wybierz dowolny wierzchołek, powiedzmy v 1 wykresu G.
Wybierz krawędź, powiedzmy e 1 z G tak, że e 1 = v 1 v 2 i v 1 ≠ v 2 ie 1 mają minimalną wagę między krawędziami padającymi na v 1 na wykresie G.
Teraz, wykonując krok 2, wybierz minimalny ważony incydent krawędzi w wersji 2 .
Kontynuuj aż do wybrania n – 1 krawędzi. Tutajn jest liczbą wierzchołków.

Minimalne drzewo opinające to -

Algorytm Kruskala
Algorytm Kruskala to zachłanny algorytm, który pomaga nam znaleźć minimalne drzewo rozpinające dla połączonego wykresu ważonego, dodając rosnące łuki kosztów na każdym kroku. Jest to algorytm minimalnego drzewa rozpinającego, który znajduje krawędź o najmniejszej możliwej wadze, która łączy dowolne dwa drzewa w lesie.
Kroki algorytmu Kruskala
Wybierz krawędź o minimalnej wadze; powiedzmy, że e 1 z wykresu G ie 1 nie jest pętlą.
Wybierz następną minimalną obciążoną krawędź połączoną z e 1 .
Kontynuuj aż do wybrania n – 1 krawędzi. Tutajn jest liczbą wierzchołków.

Minimalne drzewo rozpinające powyższego wykresu to -
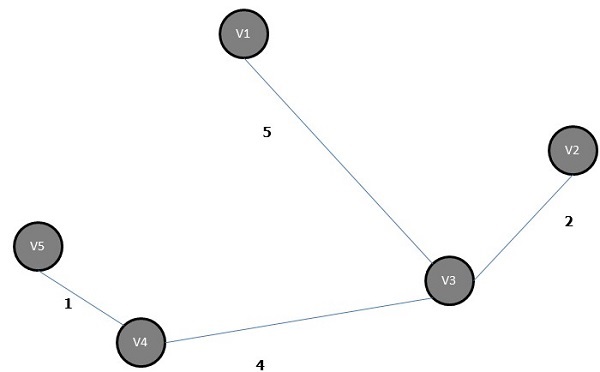
Algorytm najkrótszej ścieżki
Algorytm najkrótszej ścieżki to metoda znajdowania najmniej kosztownej ścieżki od węzła źródłowego (S) do węzła docelowego (D). Tutaj omówimy algorytm Moore'a, znany również jako algorytm pierwszego wyszukiwania szerokości.
Algorytm Moore'a
Oznacz wierzchołek źródłowy, S i oznacz go i i nastaw i=0.
Znajdź wszystkie nieoznaczone wierzchołki sąsiadujące z wierzchołkiem oznaczonym i. Jeśli żadne wierzchołki nie są połączone z wierzchołkiem, S, to wierzchołek, D, nie jest połączony z S. Jeśli są wierzchołki połączone z S, oznacz jei+1.
Jeśli oznaczono D, przejdź do kroku 4, w przeciwnym razie przejdź do kroku 2, aby zwiększyć i = i + 1.
Zatrzymaj się po znalezieniu długości najkrótszej ścieżki.