Algorytm równoległy - krótki przewodnik

Na algorithmjest sekwencją kroków, które pobierają dane wejściowe od użytkownika i po wykonaniu pewnych obliczeń generują dane wyjściowe. ZAparallel algorithm to algorytm, który może wykonywać kilka instrukcji jednocześnie na różnych urządzeniach przetwarzających, a następnie łączyć wszystkie poszczególne wyjścia w celu uzyskania końcowego wyniku.

Przetwarzanie współbieżne

Łatwa dostępność komputerów wraz z rozwojem Internetu zmieniła sposób, w jaki przechowujemy i przetwarzamy dane. Żyjemy w czasach, w których danych jest pod dostatkiem. Każdego dnia mamy do czynienia z ogromnymi ilościami danych, które wymagają skomplikowanych obliczeń i to również w krótkim czasie. Czasami musimy pobrać dane z podobnych lub powiązanych ze sobą zdarzeń, które występują jednocześnie. Właśnie tego potrzebujemyconcurrent processing które mogą podzielić złożone zadanie i przetworzyć je w wielu systemach, aby szybko uzyskać wynik.

Jednoczesne przetwarzanie jest niezbędne, gdy zadanie obejmuje przetwarzanie ogromnej ilości złożonych danych. Przykłady obejmują - dostęp do dużych baz danych, testowanie samolotów, obliczenia astronomiczne, fizykę atomową i jądrową, analizę biomedyczną, planowanie gospodarcze, przetwarzanie obrazu, robotykę, prognozowanie pogody, usługi internetowe itp.

Co to jest równoległość?

Parallelismto proces jednoczesnego przetwarzania kilku zestawów instrukcji. Zmniejsza całkowity czas obliczeniowy. Równoległość można zaimplementować za pomocąparallel computers,tj. komputer z wieloma procesorami. Komputery równoległe wymagają równoległego algorytmu, języków programowania, kompilatorów i systemu operacyjnego obsługującego wielozadaniowość.

W tym samouczku omówimy tylko parallel algorithms. Zanim przejdziemy dalej, omówmy najpierw algorytmy i ich typy.

Co to jest algorytm?

Na algorithmto sekwencja instrukcji zastosowanych w celu rozwiązania problemu. Projektując algorytm powinniśmy wziąć pod uwagę architekturę komputera, na którym algorytm będzie wykonywany. Jeśli chodzi o architekturę, istnieją dwa typy komputerów -

Komputer sekwencyjny
Komputer równoległy

W zależności od architektury komputerów mamy dwa rodzaje algorytmów -

Sequential Algorithm - Algorytm, w którym niektóre kolejne kroki instrukcji są wykonywane w porządku chronologicznym w celu rozwiązania problemu.
Parallel Algorithm- Problem jest podzielony na podproblemy i są wykonywane równolegle, aby uzyskać indywidualne wyniki. Później te indywidualne wyjścia są łączone razem, aby uzyskać ostateczną pożądaną moc.

Nie jest łatwo podzielić duży problem sub-problems. Podproblemy mogą być zależne od danych. Dlatego procesory muszą się ze sobą komunikować, aby rozwiązać problem.

Stwierdzono, że czas potrzebny procesorom na komunikowanie się ze sobą jest dłuższy niż rzeczywisty czas przetwarzania. Dlatego projektując algorytm równoległy, należy wziąć pod uwagę właściwe wykorzystanie procesora, aby uzyskać wydajny algorytm.

Aby prawidłowo zaprojektować algorytm, musimy mieć jasne pojęcie o podstawach model of computation w komputerze równoległym.

Model obliczeniowy

Zarówno komputery sekwencyjne, jak i równoległe działają na zestawie (strumieniu) instrukcji zwanych algorytmami. Ten zestaw instrukcji (algorytm) instruuje komputer, co ma zrobić na każdym kroku.

W zależności od strumienia instrukcji i strumienia danych, komputery można podzielić na cztery kategorie -

Pojedynczy strumień instrukcji, komputery z pojedynczym strumieniem danych (SISD)
Pojedynczy strumień instrukcji, komputery z wieloma strumieniami danych (SIMD)
Wiele strumieni instrukcji, komputery z pojedynczym strumieniem danych (MISD)
Wiele strumieni instrukcji, komputery z wieloma strumieniami danych (MIMD)

Komputery SISD

Komputery SISD zawierają one control unit, one processing unit, i one memory unit.

W tego typu komputerach procesor otrzymuje pojedynczy strumień instrukcji z jednostki sterującej i działa na pojedynczym strumieniu danych z jednostki pamięci. Podczas obliczeń na każdym etapie procesor otrzymuje jedną instrukcję z jednostki sterującej i operuje na pojedynczych danych odebranych z jednostki pamięci.

Komputery SIMD

Komputery SIMD zawierają one control unit, multiple processing units, i shared memory or interconnection network.

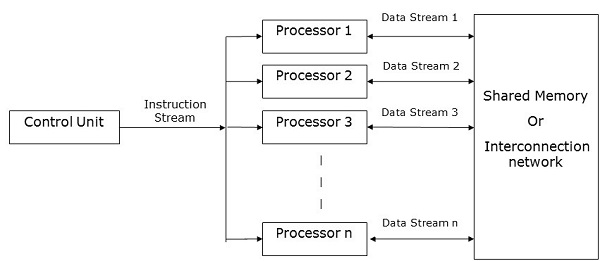
Tutaj jedna jednostka sterująca wysyła instrukcje do wszystkich jednostek przetwarzania. Podczas obliczeń na każdym kroku wszystkie procesory otrzymują pojedynczy zestaw instrukcji z jednostki sterującej i działają na innym zestawie danych z jednostki pamięci.

Każda z jednostek przetwarzających ma własną lokalną jednostkę pamięci do przechowywania zarówno danych, jak i instrukcji. W komputerach SIMD procesory muszą komunikować się między sobą. Odbywa się to przezshared memory lub przez interconnection network.

Podczas gdy niektóre procesory wykonują zestaw instrukcji, pozostałe procesory czekają na następny zestaw instrukcji. Instrukcje z jednostki sterującej decydują, który procesor będzieactive (wykonaj instrukcje) lub inactive (poczekaj na kolejną instrukcję).

Komputery MISD

Jak sama nazwa wskazuje, komputery MISD zawierają multiple control units, multiple processing units, i one common memory unit.

Tutaj każdy procesor ma własną jednostkę sterującą i mają wspólną jednostkę pamięci. Wszystkie procesory otrzymują instrukcje indywidualnie z własnej jednostki sterującej i działają na jednym strumieniu danych, zgodnie z instrukcjami otrzymanymi od odpowiednich jednostek sterujących. Ten procesor działa jednocześnie.

Komputery MIMD

Komputery MIMD mają multiple control units, multiple processing units, i a shared memory lub interconnection network.

Tutaj każdy procesor ma swoją własną jednostkę sterującą, lokalną jednostkę pamięci oraz jednostkę arytmetyczno-logiczną. Otrzymują różne zestawy instrukcji od odpowiednich jednostek sterujących i operują na różnych zestawach danych.

Uwaga

Komputer MIMD, który współużytkuje wspólną pamięć, jest znany jako multiprocessors, podczas gdy te, które korzystają z sieci połączeń, są znane jako multicomputers.
W oparciu o fizyczną odległość procesorów, multikomputery są dwojakiego rodzaju -
- Multicomputer - Gdy wszystkie procesory są bardzo blisko siebie (np. W tym samym pomieszczeniu).
- Distributed system - Gdy wszystkie procesory są daleko od siebie (np. - w różnych miastach)

Analiza algorytmu pomaga nam określić, czy algorytm jest przydatny, czy nie. Ogólnie algorytm jest analizowany na podstawie czasu jego wykonania(Time Complexity) i ilość miejsca (Space Complexity) to wymaga.

Ponieważ mamy zaawansowane urządzenia pamięci dostępne za rozsądną cenę, przestrzeń dyskowa nie jest już problemem. W związku z tym złożoność przestrzeni nie ma tak dużego znaczenia.

Algorytmy równoległe mają na celu poprawę szybkości obliczeń komputera. Aby przeanalizować algorytm równoległy, zwykle rozważamy następujące parametry -

Złożoność czasowa (czas wykonania),
Łączna liczba używanych procesorów i
Całkowity koszt.

Złożoność czasowa

Głównym powodem opracowania równoległych algorytmów było skrócenie czasu obliczeń algorytmu. Dlatego ocena czasu wykonania algorytmu jest niezwykle ważna w analizie jego wydajności.

Czas wykonania jest mierzony na podstawie czasu potrzebnego algorytmowi do rozwiązania problemu. Całkowity czas wykonania jest obliczany od momentu rozpoczęcia wykonywania algorytmu do momentu jego zatrzymania. Jeżeli wszystkie procesory nie rozpoczynają lub nie kończą wykonywania w tym samym czasie, to łączny czas wykonania algorytmu jest momentem rozpoczęcia wykonywania przez pierwszy procesor do momentu, w którym ostatni procesor przestał wykonywać swoje wykonanie.

Złożoność czasową algorytmu można podzielić na trzy kategorie:

Worst-case complexity - Gdy ilość czasu wymagana przez algorytm dla danego wejścia wynosi maximum.
Average-case complexity - Gdy ilość czasu wymagana przez algorytm dla danego wejścia wynosi average.
Best-case complexity - Gdy ilość czasu wymagana przez algorytm dla danego wejścia wynosi minimum.

Analiza asymptotyczna

Złożoność lub wydajność algorytmu to liczba kroków wykonywanych przez algorytm w celu uzyskania pożądanego wyniku. Analiza asymptotyczna jest wykonywana w celu obliczenia złożoności algorytmu w analizie teoretycznej. W analizie asymptotycznej do obliczenia funkcji złożoności algorytmu stosuje się dużą długość danych wejściowych.

Note - Asymptoticjest stanem, w którym linia ma tendencję do stykania się z krzywą, ale one się nie przecinają. Tutaj linia i krzywa są względem siebie asymptotyczne.

Notacja asymptotyczna jest najłatwiejszym sposobem opisania najszybszego i najwolniejszego możliwego czasu wykonania algorytmu wykorzystującego wysokie i niskie ograniczenia szybkości. W tym celu używamy następujących oznaczeń -

Notacja Big O.
Notacja Omega
Notacja theta

Notacja Big O.

W matematyce notacja Big O jest używana do reprezentowania asymptotycznych cech funkcji. Reprezentuje zachowanie funkcji dla dużych danych wejściowych w prostej i dokładnej metodzie. Jest to metoda reprezentacji górnej granicy czasu wykonania algorytmu. Reprezentuje najdłuższy czas, jaki algorytm może zająć, aby zakończyć swoje wykonanie. Funkcja -

f (n) = O (g (n))

jeśli istnieją stałe dodatnie c i n₀ takie że f(n) ≤ c * g(n) dla wszystkich n gdzie n ≥ n₀.

Notacja Omega

Notacja Omega to metoda reprezentacji dolnej granicy czasu wykonania algorytmu. Funkcja -

f (n) = Ω (g (n))

jeśli istnieją stałe dodatnie c i n₀ takie że f(n) ≥ c * g(n) dla wszystkich n gdzie n ≥ n₀.

Notacja Theta

Notacja theta to metoda reprezentacji zarówno dolnej, jak i górnej granicy czasu wykonania algorytmu. Funkcja -

f (n) = θ (g (n))

jeśli istnieją stałe dodatnie c₁, c₂, i n₀ takie, że c1 * g (n) ≤ f (n) ≤ c2 * g (n) dla wszystkich n gdzie n ≥ n₀.

Przyspieszenie algorytmu

Wydajność algorytmu równoległego jest określana przez obliczenie jego speedup. Przyspieszenie definiuje się jako stosunek czasu wykonania najgorszego przypadku najszybszego znanego algorytmu sekwencyjnego dla danego problemu do czasu wykonania najgorszego przypadku algorytmu równoległego.

speedup =

Czas wykonania najgorszego przypadku najszybszej znanej sekwencji dla danego problemu / Czas wykonania najgorszego przypadku algorytmu równoległego

Liczba używanych procesorów

Liczba zastosowanych procesorów jest ważnym czynnikiem w analizie wydajności algorytmu równoległego. Oblicza się koszt zakupu, utrzymania i eksploatacji komputerów. Im większa liczba procesorów wykorzystywanych przez algorytm do rozwiązania problemu, tym kosztowniejszy staje się uzyskany wynik.

Całkowity koszt

Całkowity koszt algorytmu równoległego jest iloczynem złożoności czasowej i liczby procesorów używanych w tym konkretnym algorytmie.

Całkowity koszt = złożoność czasu × liczba użytych procesorów

Dlatego też efficiency równoległego algorytmu to -

Wydajność =

Czas wykonania najgorszego przypadku algorytmu sekwencyjnego / Czas wykonania najgorszego przypadku algorytmu równoległego

Model algorytmu równoległego jest tworzony poprzez rozważenie strategii podziału danych i metody przetwarzania oraz zastosowanie odpowiedniej strategii w celu ograniczenia interakcji. W tym rozdziale omówimy następujące równoległe modele algorytmów -

Model równoległy danych
Model wykresu zadań
Model puli pracy
Model Master slave
Producent konsumenta lub model potoku
Model hybrydowy

Dane równoległe

W modelu równoległym do danych zadania są przypisane do procesów, a każde zadanie wykonuje podobne operacje na innych danych. Data parallelism jest konsekwencją pojedynczej operacji wykonywanej na wielu elementach danych.

Model równoległy do danych można zastosować w przypadku współdzielonych przestrzeni adresowych i paradygmatów przekazywania wiadomości. W modelu równoległym do danych, narzuty interakcji można zmniejszyć, wybierając lokalność zachowującą dekompozycję, stosując zoptymalizowane procedury interakcji zbiorowej lub nakładając się na siebie obliczenia i interakcje.

Podstawową cechą problemów z modelem równoległym do danych jest to, że intensywność równoległości danych rośnie wraz z rozmiarem problemu, co z kolei umożliwia wykorzystanie większej liczby procesów do rozwiązania większych problemów.

Example - Gęste mnożenie macierzy.

Model wykresu zadań

W modelu wykresu zadań równoległość jest wyrażona przez a task graph. Wykres zadań może być trywialny lub nietrywialny. W tym modelu korelacje między zadaniami są wykorzystywane do promowania lokalności lub minimalizowania kosztów interakcji. Model ten jest wymuszany do rozwiązywania problemów, w których ilość danych związanych z zadaniami jest ogromna w porównaniu z liczbą związanych z nimi obliczeń. Zadania są przydzielane w celu poprawy kosztu przenoszenia danych między zadaniami.

Examples - Równoległe szybkie sortowanie, rzadka faktoryzacja macierzy i równoległe algorytmy uzyskiwane metodą dziel i rządź.

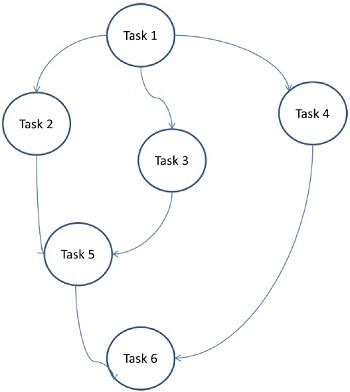
Tutaj problemy są podzielone na atomowe zadania i realizowane w postaci wykresu. Każde zadanie jest niezależną jednostką zadania, która jest zależna od co najmniej jednego zadania poprzedzającego. Po zakończeniu zadania dane wyjściowe zadania poprzedzającego są przekazywane do zadania zależnego. Zadanie z poprzednikiem rozpoczyna wykonywanie tylko wtedy, gdy całe poprzednie zadanie zostanie ukończone. Końcowy wynik wykresu jest otrzymywany po zakończeniu ostatniego zadania zależnego (Zadanie 6 na powyższym rysunku).

Model puli pracy

W modelu puli pracy zadania są dynamicznie przypisywane do procesów równoważenia obciążenia. Dlatego każdy proces może potencjalnie wykonać dowolne zadanie. Ten model jest używany, gdy ilość danych związanych z zadaniami jest stosunkowo mniejsza niż obliczenia związane z zadaniami.

Nie ma pożądanego wstępnego przypisywania zadań do procesów. Przydzielanie zadań jest scentralizowane lub zdecentralizowane. Wskaźniki do zadań są zapisywane na fizycznie udostępnianej liście, w kolejce priorytetowej lub w tabeli skrótów lub drzewie albo mogą być zapisane w fizycznie rozproszonej strukturze danych.

Zadanie może być dostępne na początku lub może być generowane dynamicznie. Jeśli zadanie jest generowane dynamicznie i odbywa się zdecentralizowane przypisywanie zadań, wymagany jest algorytm wykrywania zakończenia, aby wszystkie procesy mogły faktycznie wykryć zakończenie całego programu i przestać szukać kolejnych zadań.

Example - Równoległe wyszukiwanie drzew

Model Master-Slave

W modelu master-slave jeden lub więcej procesów nadrzędnych generuje zadanie i przydziela je do procesów podrzędnych. Zadania można przydzielić z wyprzedzeniem, jeżeli:

kapitan może oszacować wielkość zadań, lub
losowe przypisanie może wykonać zadowalające zadanie równoważenia obciążenia lub
niewolnikom przydzielane są mniejsze zadania w różnym czasie.

Ten model jest ogólnie równie odpowiedni dla shared-address-space lub message-passing paradigms, ponieważ interakcja jest naturalnie dwukierunkowa.

W niektórych przypadkach może być konieczne ukończenie zadania etapami, a zadanie w każdej fazie musi zostać ukończone, zanim będzie można wygenerować zadanie w kolejnych fazach. Model master-slave można uogólnić nahierarchical lub multi-level master-slave model w którym mistrz najwyższego poziomu przekazuje dużą część zadań do mistrza drugiego poziomu, który dalej dzieli zadania między swoich niewolników i może samodzielnie wykonać część zadania.

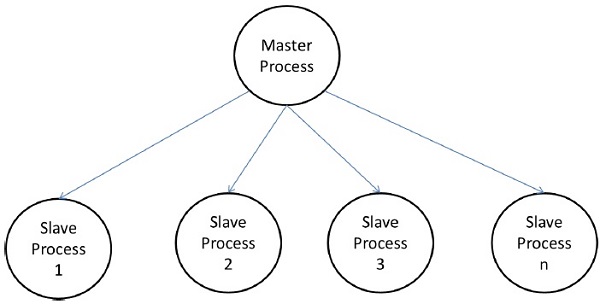
Środki ostrożności przy korzystaniu z modelu master-slave

Należy zadbać o to, aby kapitan nie stał się punktem zatoru. Może się tak zdarzyć, jeśli zadania są zbyt małe lub pracownicy są stosunkowo szybcy.

Zadania powinny być tak dobrane, aby koszt wykonania zadania przeważał nad kosztem komunikacji i kosztem synchronizacji.

Interakcja asynchroniczna może pomóc w nakładaniu się interakcji i obliczeń związanych z generowaniem pracy przez mistrza.

Model rurociągu

Jest również znany jako producer-consumer model. Tutaj zestaw danych jest przekazywany przez szereg procesów, z których każdy wykonuje na nim jakieś zadanie. Tutaj pojawienie się nowych danych powoduje wykonanie nowego zadania przez proces w kolejce. Procesy mogą tworzyć kolejkę w postaci liniowych lub wielowymiarowych tablic, drzew lub ogólnych wykresów z cyklami lub bez.

Ten model to łańcuch producentów i konsumentów. Każdy proces w kolejce można traktować jako konsumenta sekwencji elementów danych dla procesu poprzedzającego go w kolejce oraz jako producenta danych dla procesu następującego po nim w kolejce. Kolejka nie musi być łańcuchem liniowym; może to być wykres skierowany. Najpopularniejszą techniką minimalizacji interakcji stosowaną w tym modelu jest nakładanie się interakcji z obliczeniami.

Example - Równoległy algorytm faktoryzacji LU.

Modele hybrydowe

Model algorytmu hybrydowego jest wymagany, gdy do rozwiązania problemu może być potrzebny więcej niż jeden model.

Model hybrydowy może składać się z wielu modeli stosowanych hierarchicznie lub z wielu modeli stosowanych sekwencyjnie na różnych etapach równoległego algorytmu.

Example - Równoległe szybkie sortowanie

Parallel Random Access Machines (PRAM)to model uwzględniany w większości algorytmów równoległych. W tym przypadku wiele procesorów jest podłączonych do jednego bloku pamięci. Model PRAM zawiera -

Zestaw podobnego typu procesorów.
Wszystkie procesory mają wspólną jednostkę pamięci. Procesory mogą komunikować się między sobą tylko za pośrednictwem pamięci współdzielonej.
Jednostka dostępu do pamięci (MAU) łączy procesory z pojedynczą pamięcią współdzieloną.

Tutaj, n liczba procesorów może wykonywać niezależne operacje na nliczba danych w określonej jednostce czasu. Może to skutkować jednoczesnym dostępem do tej samej lokalizacji pamięci przez różne procesory.

Aby rozwiązać ten problem, w modelu PRAM narzucono następujące ograniczenia -

Exclusive Read Exclusive Write (EREW) - Tutaj żadne dwa procesory nie mogą jednocześnie czytać z tej samej lokalizacji pamięci ani zapisywać do niej.
Exclusive Read Concurrent Write (ERCW) - Tutaj żadne dwa procesory nie mogą czytać z tego samego miejsca pamięci w tym samym czasie, ale mogą zapisywać w tym samym miejscu pamięci w tym samym czasie.
Concurrent Read Exclusive Write (CREW) - Tutaj wszystkie procesory mogą czytać z tego samego miejsca pamięci w tym samym czasie, ale nie mogą zapisywać w tym samym miejscu w tym samym czasie.
Concurrent Read Concurrent Write (CRCW) - Wszystkie procesory mogą jednocześnie odczytywać lub zapisywać w tej samej lokalizacji pamięci.

Istnieje wiele metod implementacji modelu PRAM, ale najważniejsze z nich to -

Model pamięci współdzielonej
Model przekazywania wiadomości
Model równoległy danych

Model pamięci współdzielonej

Kładzie nacisk na pamięć współdzieloną control parallelism niż on data parallelism. W modelu pamięci współdzielonej wiele procesów jest wykonywanych niezależnie na różnych procesorach, ale mają one wspólną przestrzeń pamięci. Z powodu jakiejkolwiek aktywności procesora, jakiekolwiek zmiany w którejkolwiek lokalizacji pamięci są widoczne dla pozostałych procesorów.

Ponieważ wiele procesorów uzyskuje dostęp do tego samego miejsca w pamięci, może się zdarzyć, że w dowolnym momencie więcej niż jeden procesor uzyskuje dostęp do tego samego miejsca w pamięci. Załóżmy, że jeden czyta to miejsce, a drugi pisze w tym miejscu. Może to spowodować zamieszanie. Aby tego uniknąć, jakiś mechanizm kontrolny, taki jaklock / semaphore, jest wdrażana w celu zapewnienia wzajemnego wykluczenia.

Programowanie w pamięci współdzielonej zostało zaimplementowane w następujących -

Thread libraries- Biblioteka wątków zezwala na wiele wątków sterowania, które działają jednocześnie w tej samej lokalizacji pamięci. Biblioteka wątków zapewnia interfejs obsługujący wielowątkowość za pośrednictwem biblioteki podprogramów. Zawiera podprogramy dla
- Tworzenie i niszczenie wątków
- Planowanie wykonania wątku
- przekazywanie danych i wiadomości między wątkami
- zapisywanie i przywracanie kontekstów wątków

Przykłady bibliotek wątków obejmują - wątki SolarisTM dla Solaris, wątki POSIX zaimplementowane w systemie Linux, wątki Win32 dostępne w Windows NT i Windows 2000 oraz wątki JavaTM jako część standardowego zestawu JavaTM Development Kit (JDK).

Distributed Shared Memory (DSM) Systems- Systemy DSM tworzą abstrakcję pamięci współdzielonej w luźno połączonej architekturze w celu implementacji programowania pamięci współdzielonej bez wsparcia sprzętowego. Wdrażają standardowe biblioteki i wykorzystują zaawansowane funkcje zarządzania pamięcią na poziomie użytkownika obecne w nowoczesnych systemach operacyjnych. Przykłady obejmują Tread Marks System, Munin, IVY, Shasta, Brazos i Cashmere.
Program Annotation Packages- Jest to realizowane na architekturach o jednolitej charakterystyce dostępu do pamięci. Najbardziej godnym uwagi przykładem pakietów adnotacji programów jest OpenMP. OpenMP implementuje równoległość funkcjonalną. Skupia się głównie na zrównoleglaniu pętli.

Koncepcja pamięci współdzielonej zapewnia niskopoziomową kontrolę nad systemem pamięci współdzielonej, ale jest ona zwykle żmudna i błędna. Jest bardziej odpowiedni do programowania systemowego niż programowania aplikacji.

Zalety programowania w pamięci współdzielonej

Globalna przestrzeń adresowa zapewnia przyjazne dla użytkownika podejście do programowania w zakresie pamięci.
Ze względu na bliskość pamięci do procesora, udostępnianie danych między procesami jest szybkie i jednolite.
Nie ma potrzeby wyraźnego określania przekazywania danych między procesami.
Narzut komunikacji procesu jest znikomy.
Bardzo łatwo się tego nauczyć.

Wady programowania w pamięci współdzielonej

Nie jest przenośny.
Zarządzanie lokalizacją danych jest bardzo trudne.

Model przekazywania wiadomości

Przekazywanie komunikatów jest najczęściej stosowanym podejściem programowania równoległego w systemach pamięci rozproszonej. Tutaj programista musi określić równoległość. W tym modelu wszystkie procesory mają własną lokalną jednostkę pamięci i wymieniają dane za pośrednictwem sieci komunikacyjnej.

Procesory używają bibliotek przekazujących komunikaty do komunikacji między sobą. Wiadomość wraz z przesyłanymi danymi zawiera następujące elementy -

Adres procesora, z którego wysyłana jest wiadomość;
Początkowy adres lokalizacji pamięci danych w procesorze wysyłającym;
Rodzaj wysyłanych danych;
Wielkość wysyłanych danych;
Adres procesora, do którego wysyłana jest wiadomość;
Początkowy adres miejsca w pamięci dla danych w procesorze odbierającym.

Procesory mogą komunikować się ze sobą za pomocą dowolnej z następujących metod:

Komunikacja punkt-punkt
Komunikacja zbiorowa
Interfejs przekazywania wiadomości

Komunikacja punkt-punkt

Komunikacja punkt-punkt to najprostsza forma przekazywania wiadomości. W tym przypadku wiadomość może zostać wysłana z procesora wysyłającego do procesora odbierającego za pomocą dowolnego z następujących trybów przesyłania -

Synchronous mode - Następna wiadomość jest wysyłana dopiero po otrzymaniu potwierdzenia, że jej poprzednia wiadomość została dostarczona, aby zachować kolejność wiadomości.
Asynchronous mode - Aby wysłać kolejną wiadomość, nie jest wymagane otrzymanie potwierdzenia dostarczenia poprzedniej wiadomości.

Komunikacja zbiorowa

Komunikacja zbiorowa obejmuje więcej niż dwa procesory do przekazywania wiadomości. Następujące tryby umożliwiają komunikację zbiorową -

Barrier - Tryb bariery jest możliwy, jeśli wszystkie procesory uczestniczące w komunikacji uruchamiają określony blok (znany jako barrier block) do przekazywania wiadomości.
Broadcast - Nadawanie jest dwojakiego rodzaju -
- One-to-all - Tutaj jeden procesor z pojedynczą operacją wysyła ten sam komunikat do wszystkich innych procesorów.
- All-to-all - Tutaj wszystkie procesory wysyłają wiadomość do wszystkich innych procesorów.

Nadawane wiadomości mogą być trzech typów -

Personalized - Unikalne komunikaty są wysyłane do wszystkich innych procesorów docelowych.
Non-personalized - Wszystkie procesory docelowe otrzymują tę samą wiadomość.
Reduction - W przypadku rozgłaszania redukcyjnego jeden procesor w grupie zbiera wszystkie komunikaty ze wszystkich innych procesorów w grupie i łączy je w jedną wiadomość, do której mają dostęp wszystkie inne procesory w grupie.

Zalety przekazywania wiadomości

Zapewnia niskopoziomową kontrolę równoległości;
Jest przenośny;
Mniej podatne na błędy;
Mniejsze obciążenie związane z równoległą synchronizacją i dystrybucją danych.

Wady przekazywania wiadomości

W porównaniu z równoległym kodem pamięci współużytkowanej, kod przekazujący komunikaty generalnie wymaga więcej oprogramowania.

Biblioteki przekazywania wiadomości

Istnieje wiele bibliotek przekazujących wiadomości. Tutaj omówimy dwie najczęściej używane biblioteki do przekazywania wiadomości -

Interfejs przekazywania wiadomości (MPI)
Równoległa maszyna wirtualna (PVM)

Interfejs przekazywania wiadomości (MPI)

Jest to uniwersalny standard zapewniający komunikację między wszystkimi współbieżnymi procesami w rozproszonym systemie pamięci. Większość powszechnie używanych równoległych platform obliczeniowych zapewnia co najmniej jedną implementację interfejsu przekazywania wiadomości. Został zaimplementowany jako zbiór predefiniowanych funkcji o nazwielibrary i mogą być wywoływane z języków takich jak C, C ++, Fortran, itp. MPI są zarówno szybkie, jak i przenośne w porównaniu z innymi bibliotekami przekazującymi komunikaty.

Merits of Message Passing Interface

Działa tylko na architekturach pamięci współużytkowanej lub architekturach pamięci rozproszonej;
Każdy procesor ma swoje własne zmienne lokalne;
W porównaniu z dużymi komputerami z pamięcią współdzieloną, komputery z pamięcią rozproszoną są tańsze.

Demerits of Message Passing Interface

W przypadku algorytmu równoległego potrzeba więcej zmian w programowaniu;
Czasami trudne do debugowania; i
Nie działa dobrze w sieci komunikacyjnej między węzłami.

Równoległa maszyna wirtualna (PVM)

PVM to przenośny system przekazywania wiadomości, przeznaczony do łączenia oddzielnych heterogenicznych maszyn hostów w jedną maszynę wirtualną. Jest to pojedynczy, zarządzalny, równoległy zasób obliczeniowy. Duże problemy obliczeniowe, takie jak badania nadprzewodnictwa, symulacje dynamiki molekularnej i algorytmy macierzowe, można rozwiązać bardziej efektywnie kosztowo, wykorzystując pamięć i łączną moc wielu komputerów. Zarządza wszystkimi trasami komunikatów, konwersją danych, harmonogramowaniem zadań w sieci o niekompatybilnych architekturach komputerów.

Features of PVM

Bardzo łatwy w instalacji i konfiguracji;
Wielu użytkowników może korzystać z PVM w tym samym czasie;
Jeden użytkownik może wykonywać wiele aplikacji;
To mała paczka;
Obsługuje C, C ++, Fortran;
Dla danego uruchomienia programu PVM użytkownicy mogą wybrać grupę maszyn;
To model przekazywania wiadomości,
Obliczenia oparte na procesach;
Obsługuje heterogeniczną architekturę.

Programowanie równoległe danych

Głównym celem modelu programowania równoległego danych jest jednoczesne wykonywanie operacji na zbiorze danych. Zestaw danych jest zorganizowany w jakąś strukturę, taką jak tablica, hipersześcian itp. Procesory zbiorowo wykonują operacje na tej samej strukturze danych. Każde zadanie jest wykonywane na innej partycji o tej samej strukturze danych.

Jest to restrykcyjne, ponieważ nie wszystkie algorytmy można określić pod względem równoległości danych. To jest powód, dla którego równoległość danych nie jest uniwersalna.

Języki równoległe danych pomagają określić dekompozycję danych i mapowanie do procesorów. Obejmuje również instrukcje dotyczące dystrybucji danych, które pozwalają programiście mieć kontrolę nad danymi - na przykład, które dane trafią na który procesor - w celu zmniejszenia ilości komunikacji wewnątrz procesorów.

Aby poprawnie zastosować dowolny algorytm, bardzo ważne jest wybranie odpowiedniej struktury danych. Dzieje się tak, ponieważ określona operacja wykonana na strukturze danych może zająć więcej czasu w porównaniu do tej samej operacji wykonanej na innej strukturze danych.

Example- Aby uzyskać dostęp do i- ^tego elementu zestawu przy użyciu tablicy, może to zająć stały czas, ale przy użyciu połączonej listy czas wymagany do wykonania tej samej operacji może stać się wielomianem.

Dlatego wybór struktury danych musi być dokonany z uwzględnieniem architektury i rodzaju operacji do wykonania.

Następujące struktury danych są powszechnie używane w programowaniu równoległym -

Połączona lista
Arrays
Sieć Hypercube

Połączona lista

Lista połączona to struktura danych zawierająca zero lub więcej węzłów połączonych wskaźnikami. Węzły mogą, ale nie muszą, zajmować kolejne lokalizacje pamięci. Każdy węzeł ma dwie lub trzy części - jednądata part który przechowuje dane, a pozostałe dwa są link fieldsktóre przechowują adres poprzedniego lub następnego węzła. Adres pierwszego węzła jest przechowywany w zewnętrznym wskaźniku o nazwiehead. Ostatni węzeł, znany jakotail, generalnie nie zawiera żadnego adresu.

Istnieją trzy typy połączonych list -

Lista pojedynczo połączona
Lista podwójnie połączona
Lista połączona cyklicznie

Lista pojedynczo połączona

Węzeł pojedynczo połączonej listy zawiera dane i adres następnego węzła. Zewnętrzny wskaźnik o nazwiehead przechowuje adres pierwszego węzła.

Lista podwójnie połączona

Węzeł podwójnie połączonej listy zawiera dane i adres zarówno poprzedniego, jak i następnego węzła. Zewnętrzny wskaźnik o nazwiehead przechowuje adres pierwszego węzła i wywoływany wskaźnik zewnętrzny tail przechowuje adres ostatniego węzła.

Lista połączona cyklicznie

Lista połączona cyklicznie jest bardzo podobna do listy pojedynczo połączonej, z wyjątkiem faktu, że ostatni węzeł zapisał adres pierwszego węzła.

Tablice

Tablica to struktura danych, w której możemy przechowywać podobne typy danych. Może być jednowymiarowy lub wielowymiarowy. Tablice można tworzyć statycznie lub dynamicznie.

W statically declared arrays, wymiary i rozmiar tablic są znane w momencie kompilacji.
W dynamically declared arrays, wymiary i rozmiar tablicy są znane w czasie wykonywania.

Do programowania w pamięci współdzielonej tablice mogą być używane jako pamięć wspólna, a do programowania równoległego danych można ich używać poprzez partycjonowanie na pod-tablice.

Sieć Hypercube

Architektura Hypercube jest pomocna w przypadku tych równoległych algorytmów, w których każde zadanie musi komunikować się z innymi zadaniami. Topologia Hypercube może z łatwością osadzać inne topologie, takie jak pierścień i siatka. Znany jest również jako n-kostki, gdziento liczba wymiarów. Hipersześcian można skonstruować rekurencyjnie.

Wybór odpowiedniej techniki projektowania algorytmu równoległego jest najtrudniejszym i najważniejszym zadaniem. Większość problemów związanych z programowaniem równoległym może mieć więcej niż jedno rozwiązanie. W tym rozdziale omówimy następujące techniki projektowania algorytmów równoległych -

Dziel i rządź
Chciwa metoda
Programowanie dynamiczne
Backtracking
Branch & Bound
Programowanie liniowe

Metoda dziel i zwyciężaj

W podejściu dziel i rządź problem jest podzielony na kilka małych podproblemów. Następnie podproblemy są rozwiązywane rekurencyjnie i łączone w celu uzyskania rozwiązania pierwotnego problemu.

Podejście „dziel i rządź” obejmuje następujące kroki na każdym poziomie:

Divide - Pierwotny problem jest podzielony na podproblemy.
Conquer - Podproblemy są rozwiązywane rekurencyjnie.
Combine - Rozwiązania podproblemów są łączone razem, aby uzyskać rozwiązanie pierwotnego problemu.

Podejście dziel i zwyciężaj jest stosowane w następujących algorytmach -

Wyszukiwanie binarne
Szybkie sortowanie
Sortuj przez scalanie
Mnożenie liczb całkowitych
Odwrócenie macierzy
Mnożenie macierzy

Chciwa metoda

W chciwym algorytmie optymalizacji rozwiązania w dowolnym momencie wybierane jest najlepsze rozwiązanie. Chciwy algorytm jest bardzo łatwy do zastosowania do złożonych problemów. Decyduje, który krok zapewni najdokładniejsze rozwiązanie w następnym kroku.

Ten algorytm to tzw greedyponieważ po zapewnieniu optymalnego rozwiązania dla mniejszej instancji algorytm nie bierze pod uwagę całego programu jako całości. Po rozważeniu rozwiązania zachłanny algorytm nigdy więcej nie bierze pod uwagę tego samego rozwiązania.

Chciwy algorytm działa rekurencyjnie, tworząc grupę obiektów z najmniejszych możliwych części składowych. Rekurencja to procedura rozwiązywania problemu, w której rozwiązanie konkretnego problemu zależy od rozwiązania mniejszej instancji tego problemu.

Programowanie dynamiczne

Programowanie dynamiczne jest techniką optymalizacji, która dzieli problem na mniejsze podproblemy i po rozwiązaniu każdego podproblem, programowanie dynamiczne łączy wszystkie rozwiązania, aby uzyskać ostateczne rozwiązanie. W przeciwieństwie do metody dziel i rządź, programowanie dynamiczne wielokrotnie wykorzystuje rozwiązania podproblemów.

Algorytm rekurencyjny dla szeregu Fibonacciego jest przykładem programowania dynamicznego.

Algorytm cofania

Wycofywanie się to technika optymalizacji służąca do rozwiązywania problemów kombinacyjnych. Jest stosowany zarówno do problemów programowych, jak i rzeczywistych. Problem z ósemką królowej, łamigłówka Sudoku i przejście przez labirynt to popularne przykłady użycia algorytmu cofania.

W przypadku cofania zaczynamy od możliwego rozwiązania, które spełnia wszystkie wymagane warunki. Następnie przechodzimy do następnego poziomu i jeśli ten poziom nie daje satysfakcjonującego rozwiązania, wracamy o jeden poziom wstecz i zaczynamy od nowej opcji.

Rozgałęzienie i związane

Algorytm rozgałęziony i powiązany to technika optymalizacji mająca na celu uzyskanie optymalnego rozwiązania problemu. Wyszukuje najlepsze rozwiązanie dla danego problemu w całej przestrzeni rozwiązania. Granice optymalizowanej funkcji są łączone z wartością najnowszego najlepszego rozwiązania. Pozwala to algorytmowi na całkowite znalezienie części przestrzeni rozwiązania.

Celem wyszukiwania gałęzi i powiązanego jest utrzymanie najtańszej ścieżki do celu. Po znalezieniu rozwiązania można je ulepszać. Wyszukiwanie rozgałęzione i powiązane jest implementowane w wyszukiwaniu ograniczonym w głąb i przeszukiwaniu w głąb.

Programowanie liniowe

Programowanie liniowe opisuje szeroką klasę zadań optymalizacyjnych, w których zarówno kryterium optymalizacji, jak i ograniczenia są funkcjami liniowymi. Jest to technika pozwalająca uzyskać najlepszy wynik, taki jak maksymalny zysk, najkrótsza droga lub najniższy koszt.

W tym programowaniu mamy zbiór zmiennych i musimy przypisać im wartości bezwzględne, aby spełnić zestaw równań liniowych i zmaksymalizować lub zminimalizować daną liniową funkcję celu.

Macierz to zestaw danych liczbowych i nienumerycznych uporządkowanych w ustalonej liczbie wierszy i kolumn. Mnożenie macierzy jest ważnym projektem mnożenia w obliczeniach równoległych. Tutaj omówimy implementację mnożenia macierzy w różnych sieciach komunikacyjnych, takich jak siatka i hipersześcian. Mesh i hypercube mają wyższą łączność sieciową, więc pozwalają na szybszy algorytm niż inne sieci, takie jak sieć pierścieniowa.

Siatka stacji

Topologia, w której zestaw węzłów tworzy p-wymiarową siatkę, nazywana jest topologią siatki. Tutaj wszystkie krawędzie są równoległe do osi siatki i wszystkie sąsiednie węzły mogą się ze sobą komunikować.

Całkowita liczba węzłów = (liczba węzłów w rzędzie) × (liczba węzłów w kolumnie)

Sieć kratową można ocenić na podstawie następujących czynników -

Diameter
Szerokość przekroju poprzecznego

Diameter - Najdłuższy w sieci kratowej distancemiędzy dwoma węzłami jest jego średnica. P-wymiarowa sieć kratowa posiadającakP węzły mają średnicę p(k–1).

Bisection width - Szerokość podziału to minimalna liczba krawędzi, które należy usunąć z sieci, aby podzielić sieć kratową na dwie połowy.

Mnożenie macierzy za pomocą sieci kratowej

Rozważaliśmy model SIMD sieci kratowej 2D z połączeniami zawijanymi. Zaprojektujemy algorytm mnożący dwie tablice n × n przy użyciu n ² procesorów w określonym czasie.

Macierze A i B mają odpowiednio elementy a _ij i b _ij . Element przetwarzający PE _ij reprezentuje a _ij oraz b _ij . Ułóż macierze A i B w taki sposób, aby każdy procesor miał parę elementów do pomnożenia. Elementy macierzy A będą poruszać się w lewo, a elementy macierzy B będą przesuwać się w górę. Te zmiany położenia elementów w macierzy A i B przedstawiają każdemu przetwarzającemu element PE nową parę wartości do pomnożenia.

Kroki w algorytmie

Rozłóż dwie macierze.
Oblicz wszystkie produkty, a _ik × b _kj
Oblicz sumy po zakończeniu kroku 2.

Algorytm

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

Sieć Hypercube

Hipersześcian jest n-wymiarową konstrukcją, w której krawędzie są prostopadłe do siebie i mają tę samą długość. N-wymiarowy hipersześcian jest również znany jako n-sześcian lub n-wymiarowy sześcian.

Cechy Hypercube z węzłem 2 ^k

Średnica = k
Szerokość przekroju poprzecznego = 2 ^{k – 1}
Liczba krawędzi = k

Mnożenie macierzy za pomocą Hypercube Network

Ogólna specyfikacja sieci Hypercube -

Pozwolić N = 2^mbyć całkowitą liczbą procesorów. Niech procesorami będą P _0, P ₁ … ..P _N-1 .
Niech i i i ^b będą dwoma liczbami całkowitymi, 0 <i, i ^b <N-1, a jego binarna reprezentacja różni się tylko pozycją b, 0 <b <k – 1.
Rozważmy dwie macierze n × n, macierz A i macierz B.
Step 1- Elementy macierzy A i macierzy B są przypisane do n ³ procesorów w taki sposób, że procesor w pozycji i, j, k będzie miał _ji i b _ik .
Step 2 - Cały procesor na pozycji (i, j, k) oblicza iloczyn

C (i, j, k) = A (i, j, k) × B (i, j, k)
Step 3 - Suma C (0, j, k) = ΣC (i, j, k) dla 0 ≤ i ≤ n-1, gdzie 0 ≤ j, k <n – 1.

Block Matrix

Macierz blokowa lub macierz podzielona na partycje to macierz, w której każdy element sam reprezentuje indywidualną macierz. Te poszczególne sekcje są znane jakoblock lub sub-matrix.

Przykład

Na rysunku (a) X jest macierzą blokową, gdzie A, B, C, D same są macierzą. Rysunek (f) przedstawia całą macierz.

Mnożenie macierzy blokowej

Gdy dwie macierze blokowe są macierzami kwadratowymi, wówczas są mnożone tak, jak wykonujemy proste mnożenie macierzy. Na przykład,

Sortowanie to proces porządkowania elementów w grupie w określonej kolejności, tj. W kolejności rosnącej, malejącej, alfabetycznej itp. Tutaj omówimy następujące -

Sortowanie według wyliczenia
Sortowanie transpozycji nieparzyste-parzyste
Sortowanie równoległe
Hyper Quick Sort

Sortowanie listy elementów to bardzo powszechna operacja. Algorytm sortowania sekwencyjnego może nie być wystarczająco wydajny, gdy musimy sortować ogromną ilość danych. Dlatego do sortowania używane są algorytmy równoległe.

Sortowanie według wyliczenia

Sortowanie wyliczeniowe to metoda uporządkowania wszystkich elementów na liście poprzez znalezienie ostatecznej pozycji każdego elementu na posortowanej liście. Odbywa się to poprzez porównanie każdego elementu ze wszystkimi innymi elementami i znalezienie liczby elementów o mniejszej wartości.

Dlatego dla dowolnych dwóch elementów a _i oraz a _j musi być spełniony dowolny z poniższych przypadków -

a _i <a _j
a _i > a _j
a _i = a _j

Algorytm

procedure ENUM_SORTING (n)

begin
   for each process P_1,j do
      C[j] := 0;
		
   for each process P_{i, j} do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

Sortowanie transpozycji nieparzyste-parzyste

Sortowanie z transpozycją nieparzyste-parzyste jest oparte na technice sortowania bąbelkowego. Porównuje dwie sąsiednie liczby i zamienia je, jeśli pierwsza liczba jest większa niż druga, aby uzyskać listę rosnącą. Odwrotny przypadek dotyczy szeregu malejącego. Sortowanie transpozycji Odd-Even działa w dwóch fazach -odd phase i even phase. W obu fazach procesy wymieniają numery z sąsiednimi numerami po prawej stronie.

Algorytm

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

Sortowanie równoległe

Sortowanie przez scalanie najpierw dzieli nieposortowaną listę na najmniejsze możliwe listy podrzędne, porównuje ją z listą sąsiednią i scala w kolejności posortowanej. Bardzo ładnie implementuje równoległość, postępując zgodnie z algorytmem dziel i zwyciężaj.

Algorytm

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

Hyper Quick Sort

Sortowanie hiperszybkie to implementacja sortowania szybkiego na hipersześcianie. Jego kroki są następujące -

Podziel nieposortowaną listę między każdy węzeł.
Sortuj każdy węzeł lokalnie.
Z węzła 0 rozgłaszaj medianę.
Podziel każdą listę lokalnie, a następnie zamień połówki w najwyższym wymiarze.
Powtarzaj kroki 3 i 4 równolegle, aż wymiar osiągnie 0.

Algorytm

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

Wyszukiwanie jest jedną z podstawowych operacji w informatyce. Jest używany we wszystkich aplikacjach, w których musimy sprawdzić, czy element znajduje się na podanej liście, czy nie. W tym rozdziale omówimy następujące algorytmy wyszukiwania -

Dziel i rządź
Przeszukiwanie w głąb
Przeszukiwanie wszerz
Najlepsze pierwsze wyszukiwanie

Dziel i rządź

Podejście „dziel i rządź” obejmuje następujące kroki na każdym poziomie:

Divide - Pierwotny problem jest podzielony na podproblemy.
Conquer - Podproblemy są rozwiązywane rekurencyjnie.
Combine - Rozwiązania podproblemów są łączone, aby uzyskać rozwiązanie pierwotnego problemu.

Wyszukiwanie binarne jest przykładem algorytmu dziel i zwyciężaj.

Pseudo kod

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

Przeszukiwanie w głąb

Przeszukiwanie najpierw w głąb (lub DFS) to algorytm przeszukiwania struktury danych w drzewie lub nieukierunkowanym wykresie. Tutaj koncepcja polega na rozpoczęciu od węzła początkowego znanego jakorooti przejść tak daleko, jak to możliwe, w tej samej gałęzi. Jeśli otrzymamy węzeł bez kolejnego węzła, wrócimy i przejdziemy do wierzchołka, który jeszcze nie został odwiedzony.

Kroki wyszukiwania w głąb

Rozważ węzeł (root), który nie był wcześniej odwiedzany i oznacz go jako odwiedzony.
Odwiedź pierwszy sąsiedni węzeł i oznacz go jako odwiedzony.
Jeśli wszystkie kolejne węzły rozważanego węzła są już odwiedzone lub nie ma on więcej następnych węzłów, wróć do węzła nadrzędnego.

Pseudo kod

Pozwolić v być wierzchołkiem, w którym rozpoczyna się wyszukiwanie w Graph G.

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

Przeszukiwanie wszerz

Breadth-First Search (lub BFS) to algorytm przeszukiwania struktury danych w drzewie lub nieukierunkowanym wykresie. Tutaj zaczynamy od węzła, a następnie odwiedzamy wszystkie sąsiednie węzły na tym samym poziomie, a następnie przechodzimy do sąsiedniego węzła następcy na następnym poziomie. Jest to również znane jakolevel-by-level search.

Kroki przeszukiwania wszerz

Zacznij od węzła głównego, oznacz go jako odwiedzony.
Ponieważ węzeł główny nie ma węzła na tym samym poziomie, przejdź do następnego poziomu.
Odwiedź wszystkie sąsiednie węzły i oznacz je jako odwiedzone.
Przejdź do następnego poziomu i odwiedź wszystkie nieodwiedzone sąsiednie węzły.
Kontynuuj ten proces, aż wszystkie węzły zostaną odwiedzone.

Pseudo kod

Pozwolić v być wierzchołkiem, w którym rozpoczyna się wyszukiwanie w Graph G.

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

Najlepsze pierwsze wyszukiwanie

Najlepsze pierwsze wyszukiwanie to algorytm, który przechodzi przez wykres, aby dotrzeć do celu na możliwie najkrótszej ścieżce. W przeciwieństwie do BFS i DFS, Best-First Search stosuje funkcję oceny, aby określić, który węzeł jest najbardziej odpowiedni do przejścia dalej.

Kroki wyszukiwania Best-First

Zacznij od węzła głównego, oznacz go jako odwiedzony.
Znajdź następny odpowiedni węzeł i oznacz go jako odwiedzony.
Przejdź do następnego poziomu i znajdź odpowiedni węzeł i oznacz go jako odwiedzony.
Kontynuuj ten proces, aż cel zostanie osiągnięty.

Pseudo kod

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

Graf to abstrakcyjna notacja używana do reprezentowania połączenia między parami obiektów. Wykres składa się z -

Vertices- Połączone obiekty na wykresie nazywane są wierzchołkami. Wierzchołki są również znane jakonodes.
Edges - Krawędzie to łącza łączące wierzchołki.

Istnieją dwa rodzaje wykresów -

Directed graph - Na wykresie skierowanym krawędzie mają kierunek, tj. Krawędzie przechodzą od jednego wierzchołka do drugiego.
Undirected graph - Na wykresie nieukierunkowanym krawędzie nie mają kierunku.

Kolorowanie wykresu

Kolorowanie wykresu to metoda przypisywania kolorów do wierzchołków wykresu, tak aby żadne dwa sąsiednie wierzchołki nie miały tego samego koloru. Niektóre problemy z kolorowaniem wykresów to:

Vertex coloring - Sposób kolorowania wierzchołków wykresu, tak aby żadne dwa sąsiednie wierzchołki nie miały tego samego koloru.
Edge Coloring - Jest to metoda przypisywania koloru każdej krawędzi, tak aby żadne dwie sąsiednie krawędzie nie miały tego samego koloru.
Face coloring - Przypisuje kolor do każdej ściany lub regionu wykresu planarnego, tak aby żadne dwie ściany, które mają wspólną granicę, nie miały tego samego koloru.

Liczba chromatyczna

Liczba chromatyczna to minimalna liczba kolorów wymagana do pokolorowania wykresu. Na przykład liczba chromatyczna poniższego wykresu wynosi 3.

Koncepcję kolorowania grafów stosuje się przy opracowywaniu rozkładów jazdy, przydziału częstotliwości radiowych, Suduku, alokacji rejestrów i kolorowaniu map.

Kroki do kolorowania wykresów

Ustaw początkową wartość każdego procesora w tablicy n-wymiarowej na 1.
Teraz, aby przypisać określony kolor do wierzchołka, określ, czy ten kolor jest już przypisany do sąsiednich wierzchołków, czy nie.
Jeśli procesor wykryje ten sam kolor w sąsiednich wierzchołkach, ustawia jego wartość w tablicy na 0.
Po wykonaniu n ² porównań, jeśli którykolwiek element tablicy ma wartość 1, to jest to prawidłowe kolorowanie.

Pseudokod do kolorowania grafów

begin

   create the processors P(i₀,i₁,...i_n-1) where 0_i_v < m, 0 _ v < n
   status[i0,..i_n-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if a_j,k=1 and i_j=i_kthen
            status[i₀,..i_n-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Minimalne drzewo opinające

Drzewo opinające, którego suma ciężaru (lub długości) wszystkich jego krawędzi jest mniejsza niż wszystkich innych możliwych drzew rozpinających wykresu G, jest znane jako minimal spanning tree lub minimum cost spanningdrzewo. Poniższy rysunek przedstawia ważony połączony wykres.

Poniżej przedstawiono niektóre możliwe drzewa opinające z powyższego wykresu -

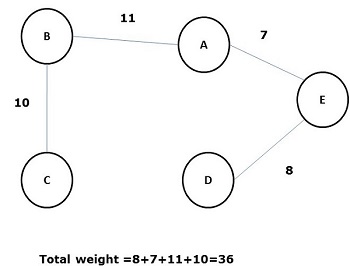
Spośród wszystkich powyższych drzew rozpinających, rysunek (d) jest minimalnym drzewem rozpinającym. Koncepcja drzewa rozpinania minimalnych kosztów jest stosowana w problemie komiwojażera, projektowaniu obwodów elektronicznych, projektowaniu wydajnych sieci i projektowaniu wydajnych algorytmów routingu.

Aby wdrożyć drzewo obejmujące minimalne koszty, stosuje się dwie następujące metody:

Algorytm Prima
Algorytm Kruskala

Algorytm Prima

Algorytm Prima to zachłanny algorytm, który pomaga nam znaleźć minimalne drzewo rozpinające dla ważonego grafu niekierowanego. Najpierw wybiera wierzchołek i znajduje krawędź o najmniejszej wadze przypadkowej na tym wierzchołku.

Kroki algorytmu Prima

Wybierz dowolny wierzchołek, powiedzmy v ₁ wykresu G.
Wybierz krawędź, powiedzmy e ₁ z G tak, że e ₁ = v ₁ v ₂ i v ₁ ≠ v ₂ ie ₁ mają minimalną wagę między krawędziami padającymi na v ₁ na wykresie G.
Teraz, wykonując krok 2, wybierz minimalny ważony incydent krawędzi w wersji ₂ .
Kontynuuj aż do wybrania n – 1 krawędzi. Tutajn jest liczbą wierzchołków.

Minimalne drzewo opinające to -

Algorytm Kruskala

Algorytm Kruskala jest chciwym algorytmem, który pomaga nam znaleźć minimalne drzewo rozpinające dla połączonego wykresu ważonego, dodając rosnące łuki kosztów na każdym kroku. Jest to algorytm minimalnego drzewa rozpinającego, który znajduje krawędź o najmniejszej możliwej wadze, która łączy dowolne dwa drzewa w lesie.

Kroki algorytmu Kruskala

Wybierz krawędź o minimalnej wadze; powiedzmy, że e ₁ z wykresu G ie ₁ nie jest pętlą.
Wybierz następną minimalną obciążoną krawędź połączoną z e ₁ .
Kontynuuj aż do wybrania n – 1 krawędzi. Tutajn jest liczbą wierzchołków.

Minimalne drzewo rozpinające powyższego wykresu to -

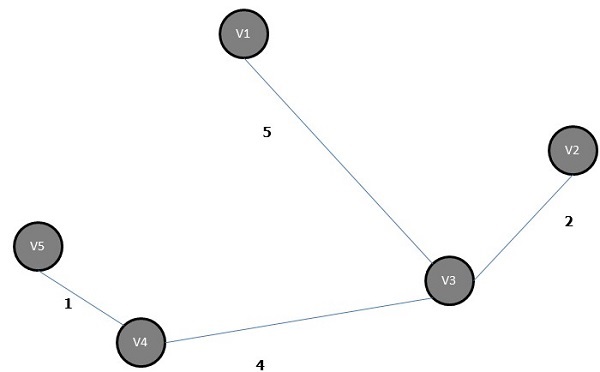
Algorytm najkrótszej ścieżki

Algorytm najkrótszej ścieżki to metoda znajdowania najmniej kosztownej ścieżki od węzła źródłowego (S) do węzła docelowego (D). Tutaj omówimy algorytm Moore'a, znany również jako algorytm pierwszego wyszukiwania szerokości.

Algorytm Moore'a

Oznacz wierzchołek źródłowy, S i oznacz go i i nastaw i=0.
Znajdź wszystkie nieopisane wierzchołki sąsiadujące z oznaczonym wierzchołkiem i. Jeśli żadne wierzchołki nie są połączone z wierzchołkiem, S, to wierzchołek, D, nie jest połączony z S. Jeśli są wierzchołki połączone z S, oznacz jei+1.
Jeśli oznaczono D, przejdź do kroku 4, w przeciwnym razie przejdź do kroku 2, aby zwiększyć i = i + 1.
Zatrzymaj się po znalezieniu długości najkrótszej ścieżki.

Algorytm równoległy - krótki przewodnik

Przetwarzanie współbieżne

Co to jest równoległość?

Co to jest algorytm?

Model obliczeniowy

Komputery SISD

Komputery SIMD

Komputery MISD

Komputery MIMD

Uwaga

Złożoność czasowa

Analiza asymptotyczna

Notacja Big O.

Notacja Omega

Notacja Theta

Przyspieszenie algorytmu

Liczba używanych procesorów

Całkowity koszt

Dane równoległe

Model wykresu zadań

Model puli pracy

Model Master-Slave

Środki ostrożności przy korzystaniu z modelu master-slave

Model rurociągu

Modele hybrydowe

Model pamięci współdzielonej

Zalety programowania w pamięci współdzielonej

Wady programowania w pamięci współdzielonej

Model przekazywania wiadomości

Komunikacja punkt-punkt

Komunikacja zbiorowa

Zalety przekazywania wiadomości

Wady przekazywania wiadomości

Biblioteki przekazywania wiadomości

Interfejs przekazywania wiadomości (MPI)

Równoległa maszyna wirtualna (PVM)

Programowanie równoległe danych

Połączona lista

Lista pojedynczo połączona

Lista podwójnie połączona

Lista połączona cyklicznie

Tablice

Sieć Hypercube

Metoda dziel i zwyciężaj

Chciwa metoda

Programowanie dynamiczne

Algorytm cofania

Rozgałęzienie i związane

Programowanie liniowe

Siatka stacji

Mnożenie macierzy za pomocą sieci kratowej

Kroki w algorytmie

Algorytm

Sieć Hypercube

Cechy Hypercube z węzłem 2 k

Mnożenie macierzy za pomocą Hypercube Network

Block Matrix

Przykład

Mnożenie macierzy blokowej

Sortowanie według wyliczenia

Algorytm

Sortowanie transpozycji nieparzyste-parzyste

Algorytm

Sortowanie równoległe

Algorytm

Hyper Quick Sort

Algorytm

Dziel i rządź

Pseudo kod

Przeszukiwanie w głąb

Kroki wyszukiwania w głąb

Pseudo kod

Przeszukiwanie wszerz

Kroki przeszukiwania wszerz

Pseudo kod

Najlepsze pierwsze wyszukiwanie

Kroki wyszukiwania Best-First

Pseudo kod

Kolorowanie wykresu

Liczba chromatyczna

Cechy Hypercube z węzłem 2 ^k