Obrazy utworzone przez lustra sferyczne
Wprowadzenie
Rysowanie diagramów promieni jest idealnym sposobem zilustrowania tworzenia obrazów przez zwierciadła sferyczne.
Przecięcie co najmniej dwóch odbitych promieni daje prawidłowe położenie obrazu obiektu punktowego.
Poniższa tabela przedstawia obraz utworzony przez plik concave mirror dla różnych położeń danego obiektu -
| Położenie obiektu | Pozycja obrazu | Rozmiar obrazu | Charakter obrazu | Wizerunek |
|---|---|---|---|---|
| W nieskończoności | W ognisku F | Mocno zmniejszone, spiczaste | Prawdziwe i odwrócone |
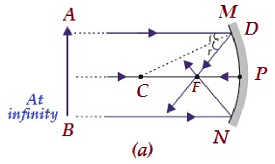
|
| Poza C | B / w F i C | Zmniejszony | Prawdziwe i odwrócone |

|
| W C | W C | Ten sam rozmiar | Prawdziwe i odwrócone |
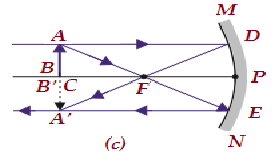
|
| Czarno-biały C i F. | Poza C | Powiększony | Prawdziwe i odwrócone |
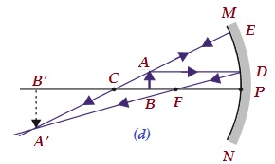
|
| W F | W nieskończoności | Bardzo powiększ | Prawdziwe i odwrócone |
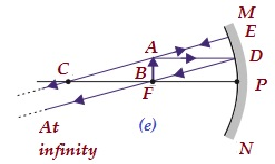
|
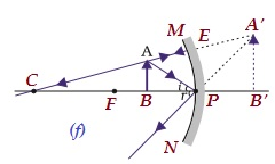
| Czarno-biały P i F. | Za lustrem | Powiększony | Wirtualne i wyprostowane |
|
Wykorzystuje wklęsłe lustro
Aby uzyskać silne równoległe wiązki światła, w latarkach, reflektorach i reflektorach samochodowych powszechnie stosuje się wklęsłe lusterka.
Lustro wklęsłe jest również używane w salonie fryzjerskim, ponieważ daje większy widok.
Lustro wklęsłe jest również używane przez dentystów do oglądania dużych obrazów zębów pacjentów.
Duże wklęsłe lustra służą do skupiania światła słonecznego w celu wytworzenia maksymalnego ciepła w piecach słonecznych.
Tworzenie obrazu przez wypukłe lustro
Poniższa tabela przedstawia obraz utworzony przez plik concave mirror dla różnych położeń danego obiektu -
| Położenie obiektu | Pozycja obrazu | Rozmiar obrazu | Charakter obrazu | Wizerunek |
|---|---|---|---|---|
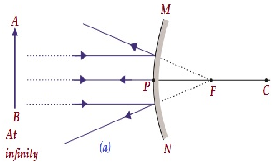
| W nieskończoności | W ognisku F, za lustrem | Bardzo mały rozmiar punktowy | Wirtualne i wyprostowane |
|
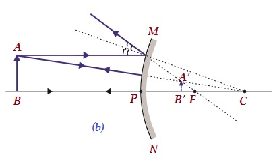
| B / w nieskończoność i biegun lustra | Czarno-biały P i F, za lustrem | Diminishe d | Wirtualne i wyprostowane |
|
Zastosowania luster wypukłych
We wszystkich pojazdach lusterka wypukłe są powszechnie stosowane jako lusterka wsteczne (boczne).
W pojazdach preferowane są lusterka wypukłe, ponieważ dają one choć pomniejszony, ale wyprostowany obraz.
Mirror Formula
Wzór jest wyrażony jako:
Formuła lustra wyraża relacje między obiektem a odległością (tj u), odległość obrazu (tj v) i ogniskową (tj. f) zwierciadła sferycznego.
$$ \ frac {1} {v} + \ frac {1} {u} = \ frac {1} {f} $$