Grafy obliczeniowe

Propagacja wsteczna jest implementowana w strukturach głębokiego uczenia, takich jak Tensorflow, Torch, Theano itp., Przy użyciu wykresów obliczeniowych. Co ważniejsze, zrozumienie propagacji wstecznej na grafach obliczeniowych łączy kilka różnych algorytmów i ich wariacji, takich jak wsteczna prop w czasie i wsteczna ze wspólnymi wagami. Gdy wszystko zostanie przekształcone w graf obliczeniowy, nadal są one tym samym algorytmem - po prostu cofają propagację na grafach obliczeniowych.

Co to jest wykres obliczeniowy

Graf obliczeniowy jest definiowany jako skierowany graf, w którym węzły odpowiadają operacjom matematycznym. Wykresy obliczeniowe są sposobem wyrażania i oceniania wyrażeń matematycznych.

Na przykład tutaj jest proste równanie matematyczne -

$$ p = x + y $$

Możemy narysować wykres obliczeniowy powyższego równania w następujący sposób.

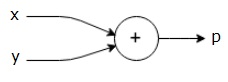
Powyższy wykres obliczeniowy ma węzeł dodawania (węzeł ze znakiem „+”) z dwiema zmiennymi wejściowymi x i y oraz jednym wyjściem q.

Weźmy inny przykład, nieco bardziej złożony. Mamy następujące równanie.

$$ g = \ left (x + y \ right) \ ast z $$

Powyższe równanie przedstawia poniższy wykres obliczeniowy.

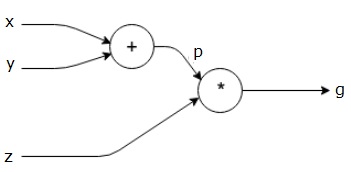
Grafy obliczeniowe i wsteczna propagacja

Grafy obliczeniowe i wsteczna propagacja są ważnymi podstawowymi koncepcjami w uczeniu głębokim do uczenia sieci neuronowych.

Podanie do przodu

Przebieg w przód to procedura oceny wartości wyrażenia matematycznego reprezentowanego przez wykresy obliczeniowe. Wykonanie przejścia do przodu oznacza, że przekazujemy wartość ze zmiennych w kierunku do przodu z lewej strony (wejście) do prawej, gdzie znajduje się dane wyjściowe.

Rozważmy przykład, nadając wartość wszystkim wejściom. Załóżmy, że wszystkie dane wejściowe mają następujące wartości.

$$ x = 1, y = 3, z = −3 $$

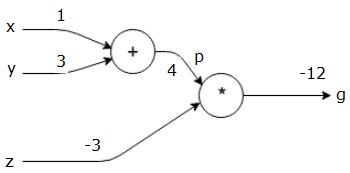
Podając te wartości wejściom, możemy wykonać przejście do przodu i uzyskać następujące wartości dla wyjść w każdym węźle.

Najpierw używamy wartości x = 1 iy = 3, aby otrzymać p = 4.

Następnie używamy p = 4 iz = -3, aby otrzymać g = -12. Przechodzimy od lewej do prawej, do przodu.

Cele przejścia wstecz

W przejściu wstecz, naszym zamiarem jest obliczenie gradientów dla każdego wejścia w odniesieniu do końcowego wyniku. Te gradienty są niezbędne do uczenia sieci neuronowej przy użyciu gradientu.

Na przykład pragniemy następujących gradientów.

Pożądane gradienty

$$ \ frac {\ częściowe x} {\ częściowe f}, \ frac {\ częściowe y} {\ częściowe f}, \ frac {\ częściowe z} {\ częściowe f} $$

Przejście wstecz (propagacja wsteczna)

Rozpoczynamy przejście wstecz od znalezienia pochodnej wyniku końcowego w odniesieniu do wyniku końcowego (siebie!). W ten sposób spowoduje to wyprowadzenie tożsamości, a wartość będzie równa jeden.

$$ \ frac {\ Part g} {\ Part g} = 1 $$

Nasz wykres obliczeniowy wygląda teraz tak, jak pokazano poniżej -

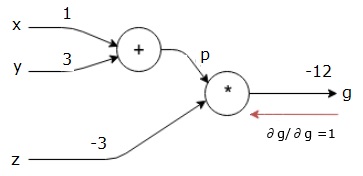
Następnie wykonamy przejście wstecz przez operację „*”. Obliczymy gradienty przy p i z. Ponieważ g = p * z, wiemy, że -

$$ \ frac {\ part g} {\ some z} = p $$

$$ \ frac {\ part g} {\ part p} = z $$

Znamy już wartości zi p z przejścia do przodu. Stąd otrzymujemy -

$$ \ frac {\ part g} {\ some z} = p = 4 $$

$$ \ frac {\ częściowe g} {\ częściowe p} = z = -3 $$

Chcemy obliczyć gradienty przy x i y -

$$ \ frac {\ Part g} {\ Part x}, \ frac {\ Part g} {\ Part y} $$

Chcemy to jednak zrobić efektywnie (chociaż na tym wykresie xig są oddalone tylko o dwa przeskoki, wyobraź sobie, że są bardzo daleko od siebie). Aby skutecznie obliczyć te wartości, użyjemy łańcuchowej reguły różniczkowania. Z reguły łańcucha mamy -

$$ \ frac {\ częściowe g} {\ częściowe x} = \ frac {\ częściowe g} {\ częściowe p} \ ast \ frac {\ częściowe p} {\ częściowe x} $$

$$ \ frac {\ częściowe g} {\ częściowe y} = \ frac {\ częściowe g} {\ częściowe p} \ ast \ frac {\ częściowe p} {\ częściowe y} $$

Ale wiemy już, że dg / dp = -3, dp / dx i dp / dy są łatwe, ponieważ p zależy bezpośrednio od x i y. Mamy -

$$$

Stąd otrzymujemy -

$$ \ frac {\ częściowe g} {\ częściowe f} = \ frac {\ częściowe g} {\ częściowe p} \ ast \ frac {\ częściowe p} {\ częściowe x} = \ left (-3 \ right) .1 = -3 $$

Dodatkowo dla wejścia y -

$$ \ frac {\ częściowe g} {\ częściowe y} = \ frac {\ częściowe g} {\ częściowe p} \ ast \ frac {\ częściowe p} {\ częściowe y} = \ left (-3 \ right) .1 = -3 $$

Głównym powodem robienia tego wstecz jest to, że kiedy musieliśmy obliczyć gradient przy x, używaliśmy tylko już obliczonych wartości i dq / dx (pochodna wyjścia węzła w odniesieniu do wejścia tego samego węzła). Wykorzystaliśmy informacje lokalne do obliczenia wartości globalnej.

Kroki do uczenia sieci neuronowej

Wykonaj następujące kroki, aby wytrenować sieć neuronową -

W przypadku punktu danych x w zbiorze danych wykonujemy przejście do przodu z x jako danymi wejściowymi i obliczamy koszt c jako dane wyjściowe.
Wykonujemy przejście wstecz zaczynając od c i obliczamy gradienty dla wszystkich węzłów na wykresie. Obejmuje to węzły, które reprezentują wagi sieci neuronowych.
Następnie aktualizujemy wagi, wykonując W = W - tempo uczenia się * gradienty.
Powtarzamy ten proces, dopóki nie zostaną spełnione kryteria zatrzymania.