Python Deep Learning - implementacje

W tej implementacji uczenia głębokiego naszym celem jest przewidywanie utraty klientów lub utraty danych dla określonego banku - którzy klienci prawdopodobnie opuszczą tę usługę bankową. Używany zestaw danych jest stosunkowo mały i zawiera 10000 wierszy z 14 kolumnami. Używamy dystrybucji Anaconda i frameworków, takich jak Theano, TensorFlow i Keras. Keras jest zbudowany na bazie Tensorflow i Theano, które działają jako jego zaplecze.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Krok 1: Wstępne przetwarzanie danych

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Krok 2

Tworzymy macierze cech zbioru danych i zmiennej docelowej, jaką jest kolumna 14, oznaczona jako „Wyjście”.

Początkowy wygląd danych jest taki, jak pokazano poniżej -

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Wynik

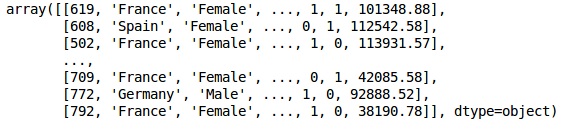
Krok 3

Y

Wynik

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Krok 4

Upraszczamy analizę, kodując zmienne typu string. Używamy funkcji ScikitLearn „LabelEncoder” do automatycznego kodowania różnych etykiet w kolumnach z wartościami od 0 do n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Wynik

W powyższym wyniku nazwy krajów są zastąpione przez 0, 1 i 2; podczas gdy mężczyzna i kobieta są zastąpieni przez 0 i 1.

Krok 5

Labelling Encoded Data

Używamy tego samego ScikitLearn biblioteka i inna funkcja o nazwie OneHotEncoder po prostu przekazać numer kolumny, tworząc zmienną zastępczą.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Teraz dwie pierwsze kolumny reprezentują kraj, a czwarta kolumna - płeć.

Wynik

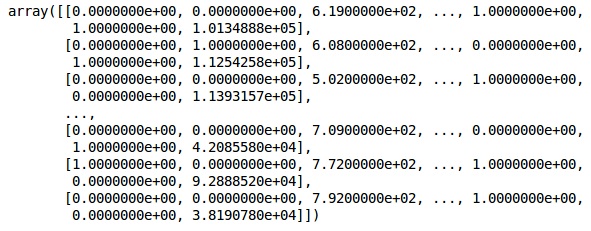
Nasze dane zawsze dzielimy na część szkoleniową i testową; trenujemy nasz model na danych uczących, a następnie sprawdzamy dokładność modelu na danych testowych, co pomaga w ocenie efektywności modelu.

Krok 6

Używamy ScikitLearn's train_test_splitfunkcji, aby podzielić nasze dane na zbiór uczący i zbiór testowy. Utrzymujemy stosunek podziału pociągu do testu na poziomie 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Niektóre zmienne mają wartości w tysiącach, a inne w dziesiątkach lub jednościach. Skalujemy dane, aby były bardziej reprezentatywne.

Krok 7

W tym kodzie dopasowujemy i przekształcamy dane szkoleniowe przy użyciu StandardScalerfunkcjonować. Standaryzujemy nasze skalowanie, abyśmy używali tej samej dopasowanej metody do przekształcania / skalowania danych testowych.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Wynik

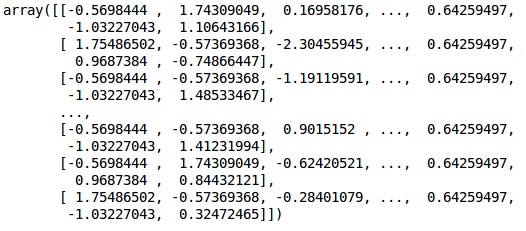
Dane są teraz poprawnie skalowane. Wreszcie mamy już za sobą wstępne przetwarzanie danych. Teraz zaczniemy od naszego modelu.

Krok 8

Tutaj importujemy wymagane moduły. Potrzebujemy modułu Sequential do inicjalizacji sieci neuronowej i modułu gęstego, aby dodać ukryte warstwy.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Krok 9

Nazwiemy model jako Klasyfikator, ponieważ naszym celem jest sklasyfikowanie odpływu klientów. Następnie używamy modułu Sequential do inicjalizacji.

#Initializing Neural Network 
classifier = Sequential()

Krok 10

Dodajemy ukryte warstwy pojedynczo za pomocą funkcji gęstej. W poniższym kodzie zobaczymy wiele argumentów.

Nasz pierwszy parametr to output_dim. Jest to liczba węzłów, które dodajemy do tej warstwy.initjest inicjalizacją Stochastic Gradient Decent. W sieci neuronowej przypisujemy wagi do każdego węzła. Podczas inicjalizacji wagi powinny być bliskie zeru, a my losowo inicjalizujemy wagi za pomocą funkcji uniform. Plikinput_dimparametr jest potrzebny tylko dla pierwszej warstwy, ponieważ model nie zna liczby naszych zmiennych wejściowych. Tutaj całkowita liczba zmiennych wejściowych wynosi 11. W drugiej warstwie model automatycznie zna liczbę zmiennych wejściowych z pierwszej warstwy ukrytej.

Wykonaj następujący wiersz kodu, aby dodać warstwę wejściową i pierwszą ukrytą warstwę -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Wykonaj następujący wiersz kodu, aby dodać drugą ukrytą warstwę -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Wykonaj następujący wiersz kodu, aby dodać warstwę wyjściową -

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Krok 11

Compiling the ANN

Do tej pory dodaliśmy wiele warstw do naszego klasyfikatora. Teraz skompilujemy je przy użyciucompilemetoda. Argumenty dodane w końcowej kontroli kompilacji uzupełniają sieć neuronową, dlatego na tym etapie musimy być ostrożni.

Oto krótkie wyjaśnienie argumentów.

Pierwszy argument to OptimizerJest to algorytm używany do znajdowania optymalnego zestawu wag. Ten algorytm nazywa sięStochastic Gradient Descent (SGD). Tutaj używamy jednego z kilku typów, zwanego „optymalizatorem Adama”. SGD zależy od straty, więc naszym drugim parametrem jest strata. Jeśli nasza zmienna zależna jest binarna, używamy logarytmicznej funkcji straty o nazwie‘binary_crossentropy’, a jeśli nasza zmienna zależna ma więcej niż dwie kategorie w danych wyjściowych, używamy ‘categorical_crossentropy’. Chcemy poprawić wydajność naszej sieci neuronowej w oparciu oaccuracywięc dodajemy metrics jako dokładność.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Krok 12

Na tym etapie należy wykonać kilka kodów.

Dopasowywanie ANN do zestawu treningowego

Teraz trenujemy nasz model na danych szkoleniowych. UżywamyfitMetoda pasująca do naszego modelu. Optymalizujemy również wagi, aby poprawić wydajność modelu. W tym celu musimy zaktualizować wagi.Batch size to liczba obserwacji, po których aktualizujemy wagi. Epochto całkowita liczba iteracji. Wartości wielkości partii i epoki są wybierane metodą prób i błędów.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Prognozowanie i ocena modelu

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Przewidywanie pojedynczej nowej obserwacji

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Krok 13

Predicting the test set result

Wynik prognozy da Ci prawdopodobieństwo odejścia klienta z firmy. Przekonwertujemy to prawdopodobieństwo na binarne 0 i 1.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Krok 14

To ostatni krok, w którym oceniamy wydajność naszego modelu. Mamy już oryginalne wyniki, dzięki czemu możemy zbudować macierz pomyłki, aby sprawdzić dokładność naszego modelu.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Wynik

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

Z macierzy pomyłki dokładność naszego modelu można obliczyć jako -

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, co jest dobre.

Algorytm propagacji do przodu

W tej sekcji nauczymy się, jak napisać kod wykonujący propagację do przodu (przewidywanie) dla prostej sieci neuronowej -

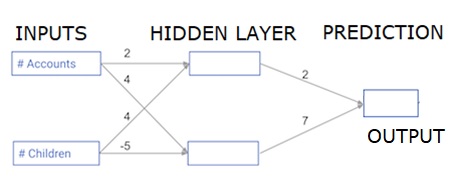
Każdy punkt danych jest klientem. Pierwsza informacja dotyczy liczby posiadanych kont, a druga - liczby dzieci. Model będzie przewidywał, ile transakcji użytkownik dokona w przyszłym roku.

Dane wejściowe są wstępnie ładowane jako dane wejściowe, a wagi znajdują się w słowniku zwanym wagami. Tablica wag dla pierwszego węzła w warstwie ukrytej jest podana odpowiednio w wagach [„node_0”], a dla drugiego węzła w warstwie ukrytej w wagach [„node_1”].

Wagi zasilające węzeł wyjściowy są dostępne w wagach.

Funkcja rektyfikowanej aktywacji liniowej

„Funkcja aktywacji” to funkcja działająca w każdym węźle. Przekształca dane wejściowe węzła w jakieś wyjście.

Prostowana liniowa funkcja aktywacji (zwana ReLU ) jest szeroko stosowana w sieciach o bardzo wysokiej wydajności. Ta funkcja przyjmuje pojedynczą liczbę jako wartość wejściową, zwracając 0, jeśli wartość wejściowa jest ujemna, i wartość wejściową jako wartość wyjściową, jeśli wartość wejściowa jest dodatnia.

Oto kilka przykładów -

• relu (4) = 4
• relu (-2) = 0

Wypełniamy definicję funkcji relu () -

• Używamy funkcji max () do obliczania wartości wyjściowej funkcji relu ().
• Stosujemy funkcję relu () do node_0_input, aby obliczyć node_0_output.
• Stosujemy funkcję relu () do node_1_input, aby obliczyć wartość node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Wynik

0.9950547536867305
-3

Stosowanie sieci do wielu obserwacji / wierszy danych

W tej sekcji dowiemy się, jak zdefiniować funkcję o nazwie Predict_with_network (). Ta funkcja wygeneruje prognozy dla wielu obserwacji danych, pobranych z sieci powyżej, przyjmowanych jako dane wejściowe. Używane są wagi podane w powyższej sieci. Używana jest również definicja funkcji relu ().

Zdefiniujmy funkcję o nazwie Predict_with_network (), która przyjmuje dwa argumenty - input_data_row i wagi - i zwraca prognozę z sieci jako wyjście.

Obliczamy wartości wejściowe i wyjściowe dla każdego węzła, przechowując je jako: node_0_input, node_0_output, node_1_input i node_1_output.

Aby obliczyć wartość wejściową węzła, mnożymy razem odpowiednie tablice i obliczamy ich sumę.

Aby obliczyć wartość wyjściową węzła, stosujemy funkcję relu () do wartości wejściowej węzła. Używamy pętli for do iteracji po danych wejściowych -

Używamy również naszej Predict_with_network () do generowania prognoz dla każdego wiersza input_data - input_data_row. Do wyników dołączamy również każdą prognozę.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Wynik

[0, 12]

Tutaj użyliśmy funkcji relu, gdzie relu (26) = 26 i relu (-13) = 0 i tak dalej.

Głębokie, wielowarstwowe sieci neuronowe

Tutaj piszemy kod, aby przeprowadzić propagację w przód dla sieci neuronowej z dwiema ukrytymi warstwami. Każda ukryta warstwa ma dwa węzły. Dane wejściowe zostały wstępnie załadowane jakoinput_data. Węzły w pierwszej ukrytej warstwie nazywane są node_0_0 i node_0_1.

Ich wagi są wstępnie ładowane jako odpowiednio wagi ['node_0_0'] i wagi ['node_0_1'].

Nazywane są węzły w drugiej ukrytej warstwie node_1_0 and node_1_1. Ich wagi są wstępnie załadowane jakoweights['node_1_0'] i weights['node_1_1'] odpowiednio.

Następnie tworzymy model wyjściowy z ukrytych węzłów przy użyciu wag wstępnie załadowanych jako weights['output'].

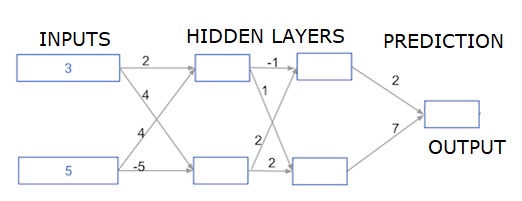
Obliczamy node_0_0_input używając jego wag ['node_0_0'] i podanych input_data. Następnie zastosuj funkcję relu (), aby uzyskać node_0_0_output.

Robimy to samo, co powyżej dla node_0_1_input, aby uzyskać node_0_1_output.

Obliczamy node_1_0_input na podstawie jego wag ['node_1_0'] i danych wyjściowych z pierwszej ukrytej warstwy - hidden_0_outputs. Następnie stosujemy funkcję relu (), aby uzyskać plik node_1_0_output.

Robimy to samo, co powyżej dla node_1_1_input, aby uzyskać node_1_1_output.

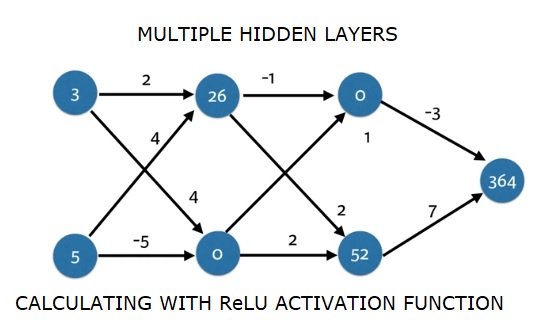
Obliczamy model_output za pomocą wag ['wyjście'] i danych wyjściowych z drugiej tablicy ukrytej warstwy ukrytej_1_outputs. Nie stosujemy funkcji relu () do tego wyjścia.

import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Wynik

364