DAA - Subsequência Comum Mais Longa

O maior problema comum de subsequência é encontrar a maior sequência que existe em ambas as strings fornecidas.

Subsequência

Vamos considerar uma sequência S = <s ₁ , s ₂ , s ₃ , s ₄ ,…, s _n >.

Uma sequência Z = <z ₁ , z ₂ , z ₃ , z ₄ ,…, z _m > sobre S é chamada de subsequência de S, se e somente se ela pode ser derivada de S deleção de alguns elementos.

Subseqüência Comum

Suponha, X e Ysão duas sequências sobre um conjunto finito de elementos. Nós podemos dizer queZ é uma subsequência comum de X e Y, E se Z é uma subsequência de ambos X e Y.

Subsequência Comum Mais Longa

Se um conjunto de sequências é dado, o maior problema de subsequência comum é encontrar uma subsequência comum de todas as sequências que tem comprimento máximo.

O mais longo problema de subsequência comum é um problema clássico de ciência da computação, a base de programas de comparação de dados como o utilitário diff, e tem aplicações em bioinformática. Ele também é amplamente utilizado por sistemas de controle de revisão, como SVN e Git, para reconciliar várias alterações feitas em uma coleção de arquivos controlada por revisão.

Método Naïve

Deixei X ser uma sequência de comprimento m e Y uma sequência de comprimento n. Verifique cada subsequência deX se é uma subsequência de Y, e retornar a maior subsequência comum encontrada.

tem 2^m subsequências de X. Testar sequências, seja ou não uma subsequência deY leva O(n)Tempo. Assim, o algoritmo ingênuo levariaO(n2^m) Tempo.

Programaçao dinamica

Sejam X = <x ₁ , x ₂ , x ₃ ,…, x _m > e Y = <y ₁ , y ₂ , y ₃ ,…, y _n > as sequências. Para calcular o comprimento de um elemento, o seguinte algoritmo é usado.

Neste procedimento, a tabela C[m, n] é calculado na ordem principal da linha e outra tabela B[m,n] é calculado para construir a solução ideal.

Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X) 
n := length(Y) 
for i = 1 to m do 
   C[i, 0] := 0 
for j = 1 to n do 
   C[0, j] := 0 
for i = 1 to m do 
   for j = 1 to n do 
      if xi = yj 
         C[i, j] := C[i - 1, j - 1] + 1 
         B[i, j] := ‘D’ 
      else 
         if C[i -1, j] ≥ C[i, j -1] 
            C[i, j] := C[i - 1, j] + 1 
            B[i, j] := ‘U’ 
         else 
         C[i, j] := C[i, j - 1]
         B[i, j] := ‘L’ 
return C and B

Algorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0 
   return  
if B[i, j] = ‘D’ 
   Print-LCS(B, X, i-1, j-1) 
   Print(xi) 
else if B[i, j] = ‘U’ 
   Print-LCS(B, X, i-1, j) 
else 
   Print-LCS(B, X, i, j-1)

Este algoritmo irá imprimir a maior subsequência comum de X e Y.

Análise

Para preencher a tabela, o for loop itera m tempos e o interior for loop itera nvezes. Portanto, a complexidade do algoritmo é O (m, n) , ondem e n têm o comprimento de duas cordas.

Exemplo

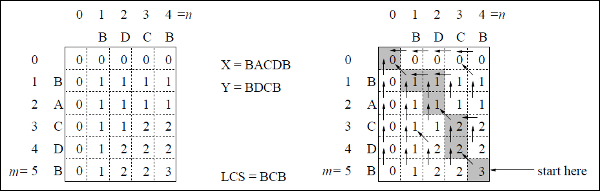
Neste exemplo, temos duas strings X = BACDB e Y = BDCB para encontrar a maior subsequência comum.

Seguindo o algoritmo LCS-Length-Table-Formulation (conforme declarado acima), calculamos a tabela C (mostrada no lado esquerdo) e a tabela B (mostrada no lado direito).

Na tabela B, em vez de 'D', 'L' e 'U', estamos usando a seta diagonal, seta para a esquerda e seta para cima, respectivamente. Após gerar a tabela B, o LCS é determinado pela função LCS-Print. O resultado é BCB.