DAA - Mesclar Classificar

Neste capítulo, discutiremos a classificação por mesclagem e analisaremos sua complexidade.

Declaração do Problema

O problema de ordenar uma lista de números se presta imediatamente a uma estratégia de dividir e conquistar: dividir a lista em duas metades, ordenar recursivamente cada metade e, em seguida, mesclar as duas sublistas ordenadas.

Solução

Neste algoritmo, os números são armazenados em uma matriz numbers[]. Aqui,p e q representa o índice inicial e final de uma submatriz.

Algorithm: Merge-Sort (numbers[], p, r) 
if p < r then  
q = ⌊(p + r) / 2⌋ 
Merge-Sort (numbers[], p, q) 
    Merge-Sort (numbers[], q + 1, r) 
    Merge (numbers[], p, q, r)

Function: Merge (numbers[], p, q, r)
n1 = q – p + 1 
n2 = r – q 
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays 
for i = 1 to n1 
   leftnums[i] = numbers[p + i - 1] 
for j = 1 to n2 
   rightnums[j] = numbers[q+ j] 
leftnums[n1 + 1] = ∞ 
rightnums[n2 + 1] = ∞ 
i = 1 
j = 1 
for k = p to r 
   if leftnums[i] ≤ rightnums[j] 
      numbers[k] = leftnums[i] 
      i = i + 1 
   else
      numbers[k] = rightnums[j] 
      j = j + 1

Análise

Vamos considerar o tempo de execução de Merge-Sort como T(n). Conseqüentemente,

$ T (n) = \ begin {cases} c & if \: n \ leqslant 1 \\ 2 \: x \: T (\ frac {n} {2}) + d \: x \: n & caso contrário \ end {cases} $ onde c e d são constantes

Portanto, usando esta relação de recorrência,

$$ T (n) = 2 ^ i T (\ frac {n} {2 ^ i}) + idn $$

Como, $ i = log \: n, \: T (n) = 2 ^ {log \: n} T (\ frac {n} {2 ^ {log \: n}}) + log \: ndn $

$ = \: cn + dnlog \: n $

Portanto, $ T (n) = O (n \: log \: n) $

Exemplo

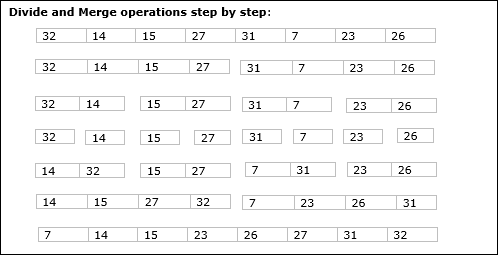
No exemplo a seguir, mostramos o algoritmo Merge-Sort passo a passo. Primeiro, cada matriz de iteração é dividida em duas submatrizes, até que a submatriz contenha apenas um elemento. Quando essas submatrizes não podem ser mais divididas, as operações de mesclagem são realizadas.