Classes NP Hard e NP-Complete
Um problema está na classe NPC se for NP e for tão hardcomo qualquer problema no NP. Um problema éNP-hard se todos os problemas em NP são redutíveis em tempo polinomial a ele, mesmo que não esteja no próprio NP.
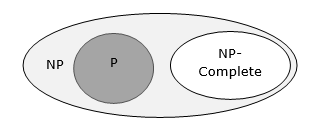
Se um algoritmo de tempo polinomial existir para qualquer um desses problemas, todos os problemas em NP seriam solucionáveis em tempo polinomial. Esses problemas são chamadosNP-complete. O fenômeno da NP-completude é importante tanto por razões teóricas quanto práticas.
Definição de NP-Completude
Uma linguagem B é NP-complete se satisfaz duas condições
B está em NP
Cada A em NP é o tempo polinomial redutível a B.
Se um idioma satisfaz a segunda propriedade, mas não necessariamente a primeira, o idioma B é conhecido como NP-Hard. Informalmente, um problema de pesquisaB é NP-Hard se existe algum NP-Complete problema A que Turing reduz a B.
O problema em NP-Hard não pode ser resolvido em tempo polinomial, até P = NP. Se for provado que um problema é NPC, não há necessidade de perder tempo tentando encontrar um algoritmo eficiente para ele. Em vez disso, podemos nos concentrar no algoritmo de aproximação de projeto.
Problemas NP-Completos
A seguir estão alguns problemas NP-Completos, para os quais nenhum algoritmo de tempo polinomial é conhecido.
- Determinar se um gráfico tem um ciclo hamiltoniano
- Determinar se uma fórmula booleana é satisfatória, etc.
Problemas NP-Difícil
Os seguintes problemas são NP-difíceis
- O problema de satisfatibilidade do circuito
- Conjunto de capa
- Capa de vértice
- Problema do caixeiro viajante
Neste contexto, agora iremos discutir o TSP é NP-Completo
TSP é NP-completo
O problema do caixeiro viajante consiste em um vendedor e um conjunto de cidades. O vendedor deve visitar cada uma das cidades partindo de uma determinada e voltando para a mesma. O desafio do problema é que o caixeiro viajante quer minimizar a duração total da viagem
Prova
Provar TSP is NP-Complete, primeiro temos que provar que TSP belongs to NP. No TSP, encontramos um passeio e verificamos se ele contém cada vértice uma vez. Em seguida, o custo total das bordas do passeio é calculado. Por fim, verificamos se o custo é mínimo. Isso pode ser concluído em tempo polinomial. portantoTSP belongs to NP.
Em segundo lugar, temos que provar que TSP is NP-hard. Para provar isso, uma maneira é mostrar queHamiltonian cycle ≤p TSP (como sabemos que o problema do ciclo hamiltoniano é NPcompleto).
Presumir G = (V, E) para ser uma instância do ciclo hamiltoniano.
Portanto, uma instância do TSP é construída. Nós criamos o gráfico completoG' = (V, E'), Onde
$$ E ^ {'} = \ lbrace (i, j) \ dois pontos i, j \ em V \: \: e \: i \ neq j $$
Assim, a função de custo é definida da seguinte forma -
$$ t (i, j) = \ begin {cases} 0 & if \: (i, j) \: \ in E \\ 1 & caso contrário \ end {cases} $$
Agora, suponha que um ciclo hamiltoniano h existe em G. É claro que o custo de cada borda emh é 0 no G' como cada borda pertence a E. Portanto,h tem um custo de 0 no G'. Assim, se o gráficoG tem um ciclo hamiltoniano, então o gráfico G' tem um tour de 0 custo.
Por outro lado, assumimos que G' tem um tour h' de custo no máximo 0. O custo das arestas emE' estão 0 e 1por definição. Portanto, cada aresta deve ter um custo de0 como o custo de h' é 0. Portanto, concluímos queh' contém apenas bordas em E.
Assim, provamos que G tem um ciclo hamiltoniano, se e somente se G' tem um tour de custo no máximo 0. O TSP é NP-completo.