Pontes AC

Neste capítulo, vamos discutir sobre as pontes CA, que podem ser usadas para medir a indutância. As pontes AC operam apenas com sinal de tensão AC. ocircuit diagram da ponte AC é mostrado na figura abaixo.

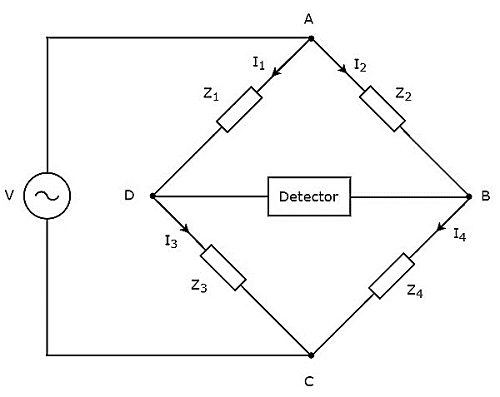
Conforme mostrado na figura acima, a ponte AC consiste principalmente em quatro braços, que são conectados em losango ou square shape. Todos esses braços consistem em alguma impedância.

O detector e a fonte de tensão CA também são necessários para encontrar o valor da impedância desconhecida. Portanto, um desses dois é colocado em uma diagonal da ponte AC e o outro é colocado na outra diagonal da ponte AC. A condição de equilíbrio da ponte de Wheatstone como -

$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

Vamos pegar o balancing condition of AC bridge, apenas substituindo R por Z na equação acima.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $

Aqui, $ Z_ {1} $ e $ Z_ {2} $ são impedâncias fixas. Considerando que $ Z_ {3} $ é uma impedância variável padrão e $ Z_ {4} $ é uma impedância desconhecida.

Note - Podemos escolher quaisquer duas dessas quatro impedâncias como impedâncias fixas, uma impedância como impedância variável padrão e a outra impedância como uma impedância desconhecida com base na aplicação.

A seguir estão as duas pontes AC, que podem ser usadas para medir inductance.

Ponte Maxwell
Hay's Bridge

Agora, vamos discutir sobre essas duas pontes AC, uma por uma.

Ponte Maxwell

A ponte de Maxwell é uma ponte AC com quatro braços, que são conectados na forma de um losango ou square shape. Dois braços desta ponte consistem em um único resistor, um braço consiste em uma combinação em série de resistor e indutor e o outro braço consiste em uma combinação paralela de resistor e capacitor.

Um detector CA e uma fonte de tensão CA são usados para encontrar o valor da impedância desconhecida. Portanto, um desses dois é colocado em uma diagonal da ponte de Maxwell e o outro é colocado na outra diagonal da ponte de Maxwell.

A ponte de Maxwell é usada para medir o valor da indutância média. ocircuit diagram da ponte de Maxwell é mostrado na figura abaixo.

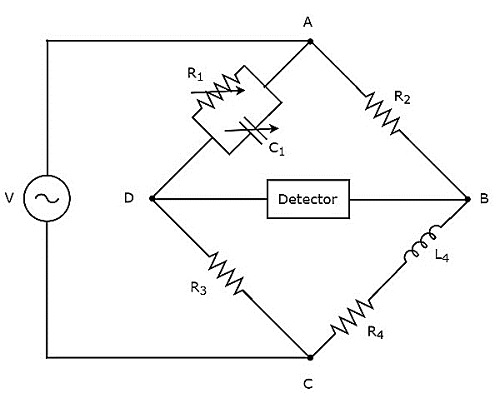
No circuito acima, os braços AB, BC, CD e DA juntos formam um losango ou forma quadrada. Os braços AB e CD consistem em resistores, $ R_ {2} $ e $ R_ {3} $ respectivamente. O braço, BC consiste em uma combinação em série de resistor, $ R_ {4} $ e indutor, $ L_ {4} $. O braço, DA consiste em uma combinação paralela de resistor, $ R_ {1} $ e capacitor, $ C_ {1} $.

Sejam $ Z_ {1}, Z_ {2}, Z_ {3} $ e $ Z_ {4} $ as impedâncias dos braços DA, AB, CD e BC respectivamente. ovalues of these impedances será

$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$

$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute esses valores de impedância na seguinte condição de equilíbrio da ponte CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)} $$

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $

De comparing os respectivos termos reais e imaginários da equação acima, obteremos

$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Equação 1

$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Equação 2

Substituindo os valores dos resistores $ R_ {1} $, $ R_ {2} $ e $ R_ {3} $ na Equação 1, obteremos o valor do resistor, $ R_ {4} $. Da mesma forma, substituindo o valor do capacitor, $ C_ {1} $ e os valores dos resistores, $ R_ {2} $ e $ R_ {3} $ na Equação 2, obteremos o valor do indutor, $ L_ {4 } $.

o advantage da ponte de Maxwell é que ambos os valores do resistor, $ R_ {4} $ e um indutor, $ L_ {4} $ são independentes do valor da frequência.

Hay's Bridge

A ponte de Hay é uma versão modificada da ponte de Maxwell, que obtemos modificando o braço, que consiste em uma combinação paralela de resistor e capacitor no braço, que consiste em uma combinação em série de resistor e capacitor na ponte de Maxwell.

A ponte de Hay é usada para medir o valor de alta indutância. ocircuit diagram da ponte de Hay é mostrado na figura abaixo.

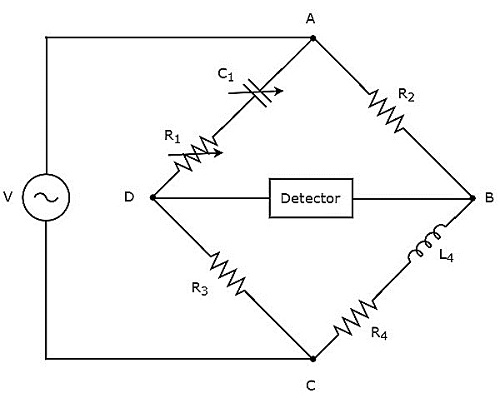
No circuito acima, os braços AB, BC, CD e DA juntos formam um losango ou forma quadrada. Os braços AB e CD consistem em resistores, $ R_ {2} $ e $ R_ {3} $ respectivamente. O braço, BC consiste em uma combinação em série de resistor, $ R_ {4} $ e indutor, $ L_ {4} $. O braço, DA consiste em uma combinação em série de resistor $ R_ {1} $ e capacitor $ C_ {1} $.

Sejam $ Z_ {1}, Z_ {2}, Z_ {3} $ e $ Z_ {4} $ as impedâncias dos braços DA, AB, CD e BC respectivamente. ovalues of these impedances será

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute esses valores de impedância na seguinte condição de equilíbrio da ponte CA.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right)} $

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $

Multiplique o numerador e o denominador do termo do lado direito da equação acima por $ 1 - j \ omega R_ {1} C_ {1} $.

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ direita)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $

De comparing os respectivos termos reais e imaginários da equação acima, obteremos

$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Equação 3

$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Equação 4

Substituindo os valores de $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ e $ \ omega $ na Equação 3 e Equação 4, obteremos os valores do resistor, $ R_ {4 } $ e indutor, $ L_ {4} $.