Lissajous Figures
Lissajous figureé o padrão que é exibido na tela, quando os sinais sinusoidais são aplicados às placas de deflexão horizontal e vertical do CRO. Esses padrões irão variar com base nas amplitudes, frequências e diferenças de fase dos sinais sinusoidais, que são aplicados às placas de deflexão horizontal e vertical do CRO.
A figura a seguir mostra um example da figura de Lissajous.
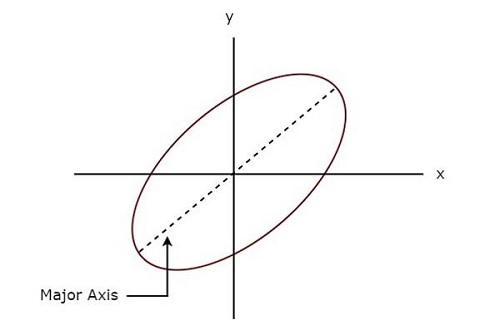
A figura de Lissajous acima está em elliptical shape e seu eixo principal tem algum ângulo de inclinação com eixo x positivo.
Medições usando figuras de Lissajous
Podemos fazer o seguinte two measurements de uma figura de Lissajous.
- Frequência do sinal sinusoidal
- Diferença de fase entre dois sinais sinusoidais
Agora, vamos discutir sobre essas duas medições, uma por uma.
Medição de frequência
A figura de Lissajous será exibida na tela, quando os sinais sinusoidais são aplicados às placas de deflexão horizontal e vertical do CRO. Portanto, aplique o sinal sinusoidal, que tem padrãoknown frequencyàs placas de deflexão horizontal do CRO. Da mesma forma, aplique o sinal sinusoidal, cujofrequency é unknown às placas de deflexão vertical do CRO
Sejam $ f_ {H} $ e $ f_ {V} $ as frequências dos sinais sinusoidais, que são aplicados às placas de deflexão horizontal e vertical do CRO, respectivamente. A relação entre $ f_ {H} $ e $ f_ {V} $ pode sermathematically representado como abaixo.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
Da relação acima, obteremos a frequência do sinal sinusoidal, que é aplicado às placas de deflexão vertical do CRO como
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (Equação 1)
Onde,
$ n_ {H} $ é o número de tangências horizontais
$ n_ {V} $ é o número de tangências verticais
Podemos encontrar os valores de $ n_ {H} $ e $ n_ {V} $ na figura de Lissajous. Assim, substituindo os valores de $ n_ {H} $, $ n_ {V} $ e $ f_ {H} $ na Equação 1, obteremos o valor de$f_{V}$, ou seja, o frequency of sinusoidal signal que é aplicado às placas de deflexão vertical do CRO.
Medição da diferença de fase
Uma figura de Lissajous é exibida na tela quando os sinais sinusoidais são aplicados às placas de deflexão horizontal e vertical do CRO. Portanto, aplique os sinais sinusoidais, que têmsame amplitude and frequency às placas de deflexão horizontal e vertical do CRO.
Para poucas figuras de Lissajous com base em sua forma, podemos dizer diretamente a diferença de fase entre os dois sinais sinusoidais.
Se a figura de Lissajous é um straight line com uma inclinação de $ 45 ^ {\ circ} $ com eixo x positivo, então o phase differenceentre os dois sinais sinusoidais será $ 0 ^ {\ circ} $. Isso significa que não há diferença de fase entre esses dois sinais sinusoidais.
Se a figura de Lissajous é um straight line com uma inclinação de $ 135 ^ {\ circ} $ com eixo x positivo, então o phase differenceentre os dois sinais sinusoidais será $ 180 ^ {\ circ} $. Isso significa que esses dois sinais sinusoidais estão fora de fase.
Se a figura de Lissajous estiver em circular shape, então a diferença de fase entre os dois sinais sinusoidais será $ 90 ^ {\ circ} $ ou $ 270 ^ {\ circ} $.
Podemos calcular a diferença de fase entre os dois sinais sinusoidais usando fórmulas, quando os números de Lissajous são de elliptical shape.
Se o eixo principal de uma figura de Lissajous de forma elíptica com um ângulo de inclinação estiver entre $ 0 ^ {\ circ} $ e $ 90 ^ {\ circ} $ com eixo x positivo, então a diferença de fase entre os dois sinais sinusoidais será.
$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$
Se o eixo principal de uma figura de Lissajous de forma elíptica com um ângulo de inclinação estiver entre $ 90 ^ {\ circ} $ e $ 180 ^ {\ circ} $ com eixo x positivo, então a diferença de fase entre os dois sinais sinusoidais será.
$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$
Where,
$ x_ {1} $ é a distância da origem ao ponto no eixo x, onde a forma elíptica de Lissajous se cruza
$ x_ {2} $ é a distância da origem à tangente vertical da forma elíptica figura de Lissajous
$ y_ {1} $ é a distância da origem ao ponto no eixo y, onde a forma elíptica de Lissajous se cruza
$ y_ {2} $ é a distância da origem até a tangente horizontal da forma elíptica figura de Lissajous
Neste capítulo, aprenderemos como encontrar a frequência de um sinal sinusoidal desconhecido e a diferença de fase entre dois sinais sinusoidais de figuras de Lissajous usando fórmulas.