Algoritmos de regressão - regressão linear
Introdução à Regressão Linear
A regressão linear pode ser definida como o modelo estatístico que analisa a relação linear entre uma variável dependente com um determinado conjunto de variáveis independentes. A relação linear entre as variáveis significa que quando o valor de uma ou mais variáveis independentes mudar (aumentar ou diminuir), o valor da variável dependente também mudará de acordo (aumentar ou diminuir).
Matematicamente, a relação pode ser representada com a ajuda da seguinte equação -
Y = mX + b
Aqui, Y é a variável dependente que estamos tentando prever
X é a variável dependente que usamos para fazer previsões.
m é a inclinação da linha de regressão que representa o efeito de X em Y
b é uma constante, conhecida como intercepto Y. Se X = 0, Y seria igual a b.
Além disso, a relação linear pode ser positiva ou negativa por natureza, conforme explicado abaixo -
Relação Linear Positiva
Uma relação linear será chamada de positiva se as variáveis independentes e dependentes aumentarem. Pode ser entendido com a ajuda do seguinte gráfico -

Relação Linear Negativa
Uma relação linear será chamada de positiva se a variável dependente aumentar e a variável dependente diminuir. Pode ser entendido com a ajuda do seguinte gráfico -

Tipos de regressão linear
A regressão linear é dos seguintes dois tipos -
- Regressão Linear Simples
- Regressão linear múltipla
Regressão Linear Simples (SLR)
É a versão mais básica da regressão linear que prevê uma resposta usando um único recurso. O pressuposto no SLR é que as duas variáveis estão linearmente relacionadas.
Implementação Python
Podemos implementar SLR em Python de duas maneiras, uma é fornecer seu próprio conjunto de dados e a outra é usar o conjunto de dados da biblioteca python scikit-learn.
Example 1 - No seguinte exemplo de implementação Python, estamos usando nosso próprio conjunto de dados.
Primeiro, vamos começar importando os pacotes necessários da seguinte maneira -
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltEm seguida, defina uma função que irá calcular os valores importantes para SLR -
def coef_estimation(x, y):A seguinte linha de script fornecerá o número de observações n -
n = np.size(x)A média do vetor x e y pode ser calculada da seguinte forma -
m_x, m_y = np.mean(x), np.mean(y)Podemos encontrar o desvio cruzado e o desvio sobre x da seguinte forma -
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xEm seguida, os coeficientes de regressão, ou seja, b podem ser calculados da seguinte forma -
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Em seguida, precisamos definir uma função que irá traçar a linha de regressão, bem como prever o vetor de resposta -
def plot_regression_line(x, y, b):A seguinte linha de script representará os pontos reais como um gráfico de dispersão -
plt.scatter(x, y, color = "m", marker = "o", s = 30)A seguinte linha de script irá prever o vetor de resposta -
y_pred = b[0] + b[1]*xAs seguintes linhas de script traçarão a linha de regressão e colocarão os rótulos nelas -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Por fim, precisamos definir a função main () para fornecer o conjunto de dados e chamar a função que definimos acima -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Resultado
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788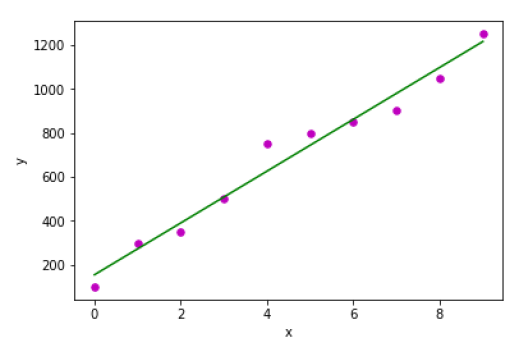
Example 2 - No seguinte exemplo de implementação Python, estamos usando o conjunto de dados de diabetes do scikit-learn.
Primeiro, vamos começar importando os pacotes necessários da seguinte maneira -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreEm seguida, vamos carregar o conjunto de dados de diabetes e criar seu objeto -
diabetes = datasets.load_diabetes()Como estamos implementando SLR, usaremos apenas um recurso da seguinte forma -
X = diabetes.data[:, np.newaxis, 2]Em seguida, precisamos dividir os dados em conjuntos de treinamento e teste da seguinte forma -
X_train = X[:-30]
X_test = X[-30:]Em seguida, precisamos dividir o alvo em conjuntos de treinamento e teste da seguinte forma -
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Agora, para treinar o modelo, precisamos criar um objeto de regressão linear da seguinte maneira -
regr = linear_model.LinearRegression()Em seguida, treine o modelo usando os conjuntos de treinamento da seguinte forma -
regr.fit(X_train, y_train)Em seguida, faça previsões usando o conjunto de testes da seguinte forma -
y_pred = regr.predict(X_test)Em seguida, imprimiremos alguns coeficientes como MSE, pontuação de variância, etc., como segue -
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Agora, plote as saídas da seguinte forma -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Resultado
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Regressão Linear Múltipla (MLR)
É a extensão da regressão linear simples que prevê uma resposta usando dois ou mais recursos. Matematicamente, podemos explicar da seguinte forma -
Considere um conjunto de dados com n observações, p características, ou seja, variáveis independentes ey como uma resposta, ou seja, variável dependente, a linha de regressão para p características pode ser calculada como segue -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$Aqui, h (x i ) é o valor de resposta previsto e b 0 , b 1 , b 2 …, b p são os coeficientes de regressão.
Modelos de regressão linear múltipla sempre incluem os erros nos dados conhecidos como erro residual que altera o cálculo da seguinte forma -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$Também podemos escrever a equação acima da seguinte forma -
$$ y_ {i} = h (x_ {i}) + e_ {i} \: ou \: e_ {i} = y_ {i} - h (x_ {i}) $$Implementação Python
neste exemplo, usaremos o conjunto de dados de habitação de Boston do scikit learn -
Primeiro, vamos começar importando os pacotes necessários da seguinte maneira -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsEm seguida, carregue o conjunto de dados da seguinte forma -
boston = datasets.load_boston(return_X_y=False)As seguintes linhas de script definirão a matriz de recursos, X e vetor de resposta, Y -
X = boston.data
y = boston.targetEm seguida, divida o conjunto de dados em conjuntos de treinamento e teste da seguinte maneira -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Exemplo
Agora, crie um objeto de regressão linear e treine o modelo da seguinte maneira -
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Resultado
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
Suposições
A seguir estão algumas suposições sobre o conjunto de dados feito pelo modelo de regressão linear -
Multi-collinearity- O modelo de regressão linear assume que há muito pouca ou nenhuma multicolinearidade nos dados. Basicamente, a multicolinearidade ocorre quando as variáveis independentes ou recursos têm dependência neles.
Auto-correlation- Outra hipótese que o modelo de regressão linear assume é que há muito pouca ou nenhuma autocorrelação nos dados. Basicamente, a autocorrelação ocorre quando há dependência entre erros residuais.
Relationship between variables - O modelo de regressão linear assume que a relação entre as variáveis de resposta e recursos deve ser linear.