Мосты переменного тока
В этой главе давайте обсудим мосты переменного тока, которые можно использовать для измерения индуктивности. Мосты переменного тока работают только с сигналом переменного напряжения. Вcircuit diagram моста переменного тока показан на рисунке ниже.
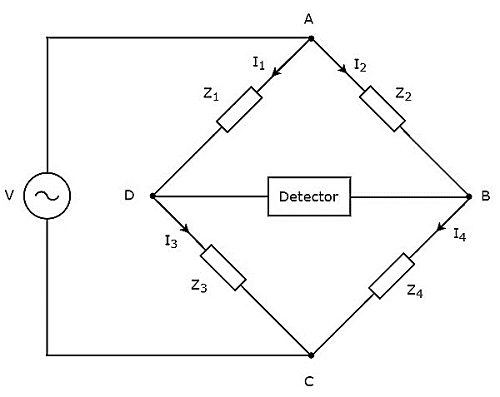
Как показано на рисунке выше, мост переменного тока в основном состоит из четырех плеч, которые соединены ромбом или square shape. Все эти руки состоят из некоторого сопротивления.
Детектор и источник переменного напряжения также необходимы, чтобы найти значение неизвестного импеданса. Следовательно, один из этих двух размещается на одной диагонали моста переменного тока, а другой - на другой диагонали моста переменного тока. Состояние балансировки моста Уитстона как -
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
Мы получим balancing condition of AC bridge, просто заменив R на Z в приведенном выше уравнении.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
Здесь $ Z_ {1} $ и $ Z_ {2} $ - фиксированные импедансы. Принимая во внимание, что $ Z_ {3} $ - это стандартный переменный импеданс, а $ Z_ {4} $ - неизвестный импеданс.
Note - Мы можем выбрать любые два из этих четырех импедансов в качестве фиксированных сопротивлений, один импеданс в качестве стандартного переменного импеданса и другой импеданс в качестве неизвестного импеданса в зависимости от приложения.
Ниже приведены два моста переменного тока, которые можно использовать для измерения inductance.
- Мост Максвелла
- Hay's Bridge
Теперь давайте поговорим об этих двух мостах переменного тока один за другим.
Мост Максвелла
Мост Максвелла представляет собой мост переменного тока, имеющий четыре плеча, которые соединяются в форме ромба или square shape. Два плеча этого моста состоят из одного резистора, одно плечо состоит из последовательной комбинации резистора и индуктора, а другое плечо состоит из параллельной комбинации резистора и конденсатора.
Детектор переменного тока и источник переменного напряжения используются для определения значения неизвестного импеданса. Следовательно, один из этих двух размещается на одной диагонали моста Максвелла, а другой - на другой диагонали моста Максвелла.
Мост Максвелла используется для измерения значения средней индуктивности. Вcircuit diagram моста Максвелла показан на рисунке ниже.
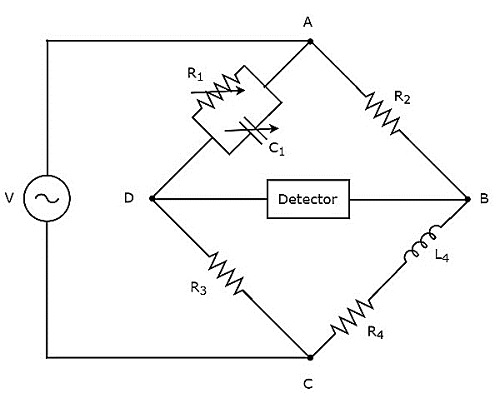
В приведенной выше схеме руки AB, BC, CD и DA вместе образуют ромб или квадрат. Плечи AB и CD состоят из резисторов $ R_ {2} $ и $ R_ {3} $ соответственно. Плечо BC состоит из последовательной комбинации резистора $ R_ {4} $ и катушки индуктивности $ L_ {4} $. Плечо DA состоит из параллельной комбинации резистора $ R_ {1} $ и конденсатора $ C_ {1} $.
Пусть $ Z_ {1}, Z_ {2}, Z_ {3} $ и $ Z_ {4} $ - импедансы плеч DA, AB, CD и BC соответственно. Вvalues of these impedances будет
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute эти значения импеданса в следующих условиях балансировки моста переменного тока.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1}) C_ {1}}} \ right)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
От comparing соответствующие действительные и мнимые члены приведенного выше уравнения, мы получим
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Уравнение 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Уравнение 2
Подставляя значения резисторов $ R_ {1} $, $ R_ {2} $ и $ R_ {3} $ в уравнение 1, мы получим значение резистора $ R_ {4} $. Точно так же, подставив значение конденсатора $ C_ {1} $ и значения резисторов $ R_ {2} $ и $ R_ {3} $ в уравнение 2, мы получим значение индуктора $ L_ {4 } $.
В advantage моста Максвелла состоит в том, что оба значения резистора $ R_ {4} $ и индуктора $ L_ {4} $ не зависят от значения частоты.
Hay's Bridge
Мост Хэя - это модифицированная версия моста Максвелла, которую мы получаем путем модификации плеча, который состоит из параллельной комбинации резистора и конденсатора в плече, который состоит из последовательной комбинации резистора и конденсатора в мосте Максвелла.
Мост Хэя используется для измерения значения высокой индуктивности. Вcircuit diagram моста Хэя показано на рисунке ниже.
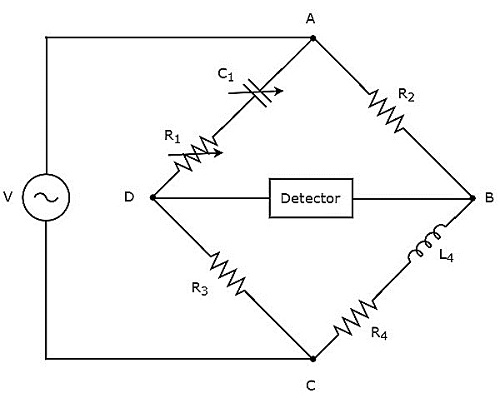
В приведенной выше схеме руки AB, BC, CD и DA вместе образуют ромб или квадрат. Плечи AB и CD состоят из резисторов $ R_ {2} $ и $ R_ {3} $ соответственно. Плечо BC состоит из последовательной комбинации резистора $ R_ {4} $ и катушки индуктивности $ L_ {4} $. Плечо DA состоит из последовательной комбинации резистора $ R_ {1} $ и конденсатора $ C_ {1} $.
Пусть $ Z_ {1}, Z_ {2}, Z_ {3} $ и $ Z_ {4} $ - импедансы плеч DA, AB, CD и BC соответственно. Вvalues of these impedances будет
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute эти значения импеданса в следующих условиях балансировки моста переменного тока.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ омега C_ {1}} \ right)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $
Умножьте числитель и знаменатель члена правой части приведенного выше уравнения на $ 1 - j \ omega R_ {1} C_ {1} $.
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ омега R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
От comparing соответствующие действительные и мнимые члены приведенного выше уравнения, мы получим
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Уравнение 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Уравнение 4
Подставляя значения $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ и $ \ omega $ в уравнение 3 и 4, мы получим значения резистора $ R_ {4 } $ и индуктор $ L_ {4} $.