Scikit Learn - Краткое руководство

В этой главе мы поймем, что такое Scikit-Learn или Sklearn, происхождение Scikit-Learn и некоторые другие связанные темы, такие как сообщества и участники, ответственные за разработку и обслуживание Scikit-Learn, его предварительные условия, установку и его функции.

Что такое Scikit-Learn (Sklearn)

Scikit-learn (Sklearn) - самая полезная и надежная библиотека для машинного обучения на Python. Он предоставляет набор эффективных инструментов для машинного обучения и статистического моделирования, включая классификацию, регрессию, кластеризацию и уменьшение размерности через интерфейс согласованности в Python. Эта библиотека, которая в основном написана на Python, построена наNumPy, SciPy и Matplotlib.

Происхождение Scikit-Learn

Первоначально он назывался scikits.learn и первоначально был разработан Дэвидом Курнапо как проект Google Summer of Code в 2007 году. Позже, в 2010 году, Фабиан Педрегоса, Гаэль Вароко, Александр Грамфор и Винсент Мишель из FIRCA (Французский институт исследований в области компьютерных наук и автоматизации) приняли этот проект находится на другом уровне и сделал первый публичный релиз (v0.1 beta) 1 февраля 2010 года.

Давайте посмотрим на его историю версий -

• Май 2019: scikit-learn 0.21.0

• Март 2019: scikit-learn 0.20.3

• Декабрь 2018: scikit-learn 0.20.2

• Ноябрь 2018: scikit-learn 0.20.1

• Сентябрь 2018: scikit-learn 0.20.0

• Июль 2018: scikit-learn 0.19.2

• Июль 2017: scikit-learn 0.19.0

• Сентябрь 2016 г. scikit-learn 0.18.0

• Ноябрь 2015 г. scikit-learn 0.17.0

• Март 2015 г. scikit-learn 0.16.0

• Июль 2014 г. scikit-learn 0.15.0

• Август 2013. scikit-learn 0.14.

Сообщество и участники

Scikit-learn - это работа сообщества, и каждый может внести в нее свой вклад. Этот проект размещен наhttps://github.com/scikit-learn/scikit-learn. Следующие люди в настоящее время являются основными участниками разработки и поддержки Sklearn:

• Йорис Ван ден Босше (специалист по данным)

• Томас Джей Фан (разработчик программного обеспечения)

• Александр Грамфор (исследователь машинного обучения)

• Оливье Гризель (эксперт по машинному обучению)

• Николас Хуг (младший научный сотрудник)

• Андреас Мюллер (специалист по машинному обучению)

• Ханьминь Цинь (инженер-программист)

• Адрин Джалали (разработчик открытого исходного кода)

• Нелле Варокуо (научный сотрудник)

• Роман Юрчак (Data Scientist)

Различные организации, такие как Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify и многие другие, используют Sklearn.

Предпосылки

Прежде чем мы начнем использовать последнюю версию scikit-learn, нам потребуется следующее:

• Python (> = 3,5)

• NumPy (> = 1.11.0)

• Scipy (> = 0,17,0) li

• Джоблиб (> = 0,11)

• Matplotlib (> = 1.5.1) требуется для возможностей построения графиков Sklearn.

• Pandas (> = 0.18.0) требуется для некоторых примеров scikit-learn с использованием структуры данных и анализа.

Установка

Если вы уже установили NumPy и Scipy, ниже приведены два самых простых способа установить scikit-learn:

Использование pip

Следующую команду можно использовать для установки scikit-learn через pip -

pip install -U scikit-learn

Использование conda

Следующую команду можно использовать для установки scikit-learn через conda -

conda install scikit-learn

С другой стороны, если NumPy и Scipy еще не установлены на вашей рабочей станции Python, вы можете установить их, используя либо pip или же conda.

Еще один вариант использования scikit-learn - использовать такие дистрибутивы Python, как Canopy и Anaconda потому что они оба поставляют последнюю версию scikit-learn.

Особенности

Вместо того, чтобы сосредоточиться на загрузке, манипулировании и суммировании данных, библиотека Scikit-learn сосредоточена на моделировании данных. Некоторые из самых популярных групп моделей, предоставляемых Sklearn, следующие:

Supervised Learning algorithms - Почти все популярные алгоритмы контролируемого обучения, такие как линейная регрессия, машина опорных векторов (SVM), дерево решений и т. Д., Являются частью scikit-learn.

Unsupervised Learning algorithms - С другой стороны, в нем также есть все популярные алгоритмы неконтролируемого обучения, от кластеризации, факторного анализа, PCA (анализа главных компонентов) до неконтролируемых нейронных сетей.

Clustering - Эта модель используется для группировки немаркированных данных.

Cross Validation - Используется для проверки точности контролируемых моделей на невидимых данных.

Dimensionality Reduction - Он используется для уменьшения количества атрибутов в данных, которые в дальнейшем можно использовать для обобщения, визуализации и выбора функций.

Ensemble methods - Как следует из названия, он используется для объединения прогнозов нескольких контролируемых моделей.

Feature extraction - Он используется для извлечения функций из данных для определения атрибутов в данных изображения и текста.

Feature selection - Он используется для определения полезных атрибутов для создания контролируемых моделей.

Open Source - Это библиотека с открытым исходным кодом, которую также можно использовать в коммерческих целях по лицензии BSD.

В этой главе рассматривается процесс моделирования в Sklearn. Давайте разберемся примерно с тем же подробнее и начнем с загрузки набора данных.

Загрузка набора данных

Набор данных называется набором данных. Он имеет следующие два компонента -

Features- Переменные данных называются его характеристиками. Они также известны как предикторы, входные данные или атрибуты.

• Feature matrix - Это набор функций, если их несколько.

• Feature Names - Это список всех названий функций.

Response- Это выходная переменная, которая в основном зависит от переменных функции. Они также известны как цель, метка или выход.

• Response Vector- Используется для представления столбца ответа. Обычно у нас есть только один столбец ответов.

• Target Names - Это возможные значения, принимаемые вектором ответа.

В Scikit-learn есть несколько примеров наборов данных, например iris и digits для классификации и Boston house prices для регресса.

пример

Ниже приведен пример загрузки iris набор данных -

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])

Вывод

Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
   [5.1 3.5 1.4 0.2]
   [4.9 3. 1.4 0.2]
   [4.7 3.2 1.3 0.2]
   [4.6 3.1 1.5 0.2]
   [5. 3.6 1.4 0.2]
   [5.4 3.9 1.7 0.4]
   [4.6 3.4 1.4 0.3]
   [5. 3.4 1.5 0.2]
   [4.4 2.9 1.4 0.2]
   [4.9 3.1 1.5 0.1]
]

Разделение набора данных

Чтобы проверить точность нашей модели, мы можем разделить набор данных на две части:a training set и a testing set. Используйте обучающий набор для обучения модели и тестовый набор для тестирования модели. После этого мы можем оценить, насколько хорошо работает наша модель.

пример

В следующем примере данные будут разделены на соотношение 70:30, т.е. 70% данных будут использоваться в качестве данных обучения, а 30% - в качестве данных тестирования. Набор данных - это набор данных радужной оболочки глаза, как в примере выше.

from sklearn.datasets import load_iris
iris = load_iris()

X = iris.data
y = iris.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
   X, y, test_size = 0.3, random_state = 1
)

print(X_train.shape)
print(X_test.shape)

print(y_train.shape)
print(y_test.shape)

Вывод

(105, 4)
(45, 4)
(105,)
(45,)

Как видно из приведенного выше примера, он использует train_test_split()функция scikit-learn для разделения набора данных. Эта функция имеет следующие аргументы -

• X, y - Здесь, X это feature matrix а y - это response vector, которые нужно разделить.

• test_size- Представляет собой отношение тестовых данных к общему количеству данных. Как и в приведенном выше примере, мы устанавливаемtest_data = 0.3 для 150 строк X. Это даст тестовые данные размером 150 * 0,3 = 45 строк.

• random_size- Используется для гарантии того, что раскол всегда будет одинаковым. Это полезно в ситуациях, когда вы хотите получить воспроизводимые результаты.

Обучите модель

Затем мы можем использовать наш набор данных для обучения некоторой модели прогнозирования. Как уже говорилось, scikit-learn имеет широкий диапазонMachine Learning (ML) algorithms которые имеют согласованный интерфейс для настройки, прогнозирования точности, отзыва и т. д.

пример

В приведенном ниже примере мы собираемся использовать классификатор KNN (K ближайших соседей). Не вдавайтесь в подробности алгоритмов KNN, для этого будет отдельная глава. Этот пример используется только для понимания части реализации.

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
   X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data

sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)

Вывод

Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']

Сохранение модели

После обучения модели желательно, чтобы она сохранялась для будущего использования, чтобы нам не приходилось повторно обучать ее снова и снова. Это можно сделать с помощьюdump и load особенности joblib пакет.

Рассмотрим приведенный ниже пример, в котором мы будем сохранять обученную выше модель (classifier_knn) для будущего использования -

from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')

Приведенный выше код сохранит модель в файле iris_classifier_knn.joblib. Теперь объект можно перезагрузить из файла с помощью следующего кода -

joblib.load('iris_classifier_knn.joblib')

Предварительная обработка данных

Поскольку мы имеем дело с большим количеством данных, и эти данные находятся в необработанном виде, перед вводом этих данных в алгоритмы машинного обучения нам необходимо преобразовать их в значимые данные. Этот процесс называется предварительной обработкой данных. Scikit-learn имеет пакет с именемpreprocessingдля этого. Вpreprocessing пакет имеет следующие методы -

Бинаризация

Этот метод предварительной обработки используется, когда нам нужно преобразовать наши числовые значения в логические значения.

пример

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [2.1, -1.9, 5.5],
   [-1.5, 2.4, 3.5],
   [0.5, -7.9, 5.6],
   [5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)

В приведенном выше примере мы использовали threshold value = 0,5, и поэтому все значения выше 0,5 будут преобразованы в 1, а все значения ниже 0,5 будут преобразованы в 0.

Вывод

Binarized data:
[
   [ 1. 0. 1.]
   [ 0. 1. 1.]
   [ 0. 0. 1.]
   [ 1. 1. 0.]
]

Среднее удаление

Этот метод используется для исключения среднего значения из вектора признаков, чтобы центр каждого объекта был нулевым.

пример

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [2.1, -1.9, 5.5],
   [-1.5, 2.4, 3.5],
   [0.5, -7.9, 5.6],
   [5.9, 2.3, -5.8]]
)

#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data

data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))

Вывод

Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]

Масштабирование

Мы используем эту технику предварительной обработки для масштабирования векторов признаков. Масштабирование векторов признаков важно, поскольку объекты не должны быть синтетически большими или маленькими.

пример

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)

Вывод

Min max scaled data:
[
   [ 0.48648649 0.58252427 0.99122807]
   [ 0. 1. 0.81578947]
   [ 0.27027027 0. 1. ]
   [ 1. 0.99029126 0. ]
]

Нормализация

Мы используем эту технику предварительной обработки для изменения векторов признаков. Нормализация векторов признаков необходима для того, чтобы векторы признаков можно было измерить в обычном масштабе. Существует два типа нормализации:

L1 нормализация

Его также называют наименьшими абсолютными отклонениями. Он изменяет значение таким образом, что сумма абсолютных значений всегда остается до 1 в каждой строке. В следующем примере показана реализация нормализации L1 для входных данных.

пример

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)

Вывод

L1 normalized data:
[
   [ 0.22105263 -0.2 0.57894737]
   [-0.2027027 0.32432432 0.47297297]
   [ 0.03571429 -0.56428571 0.4 ]
   [ 0.42142857 0.16428571 -0.41428571]
]

L2 нормализация

Также называется методом наименьших квадратов. Он изменяет значение таким образом, что сумма квадратов всегда остается до 1 в каждой строке. В следующем примере показана реализация нормализации L2 для входных данных.

пример

import numpy as np
from sklearn import preprocessing
Input_data = np.array(
   [
      [2.1, -1.9, 5.5],
      [-1.5, 2.4, 3.5],
      [0.5, -7.9, 5.6],
      [5.9, 2.3, -5.8]
   ]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)

Вывод

L2 normalized data:
[
   [ 0.33946114 -0.30713151 0.88906489]
   [-0.33325106 0.53320169 0.7775858 ]
   [ 0.05156558 -0.81473612 0.57753446]
   [ 0.68706914 0.26784051 -0.6754239 ]
]

Как мы знаем, машинное обучение собирается создать модель из данных. Для этого компьютер должен сначала понять данные. Далее мы собираемся обсудить различные способы представления данных, чтобы их мог понять компьютер.

Данные в виде таблицы

Лучший способ представления данных в Scikit-learn - в виде таблиц. Таблица представляет собой двумерную сетку данных, где строки представляют отдельные элементы набора данных, а столбцы представляют количества, связанные с этими отдельными элементами.

пример

В примере, приведенном ниже, мы можем скачать iris dataset в виде Pandas DataFrame с помощью python seaborn библиотека.

import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()

Вывод

sepal_length sepal_width petal_length petal_width  species
0        5.1      3.5         1.4             0.2   setosa
1        4.9      3.0         1.4             0.2   setosa
2        4.7      3.2         1.3             0.2   setosa
3        4.6      3.1         1.5             0.2   setosa
4        5.0      3.6         1.4             0.2   setosa

Из вышеприведенного вывода мы видим, что каждая строка данных представляет один наблюдаемый цветок, а количество строк представляет собой общее количество цветов в наборе данных. Обычно мы называем строки матрицы образцами.

С другой стороны, каждый столбец данных представляет количественную информацию, описывающую каждый образец. Обычно мы называем столбцы матрицы функциями.

Данные как матрица признаков

Матрица характеристик может быть определена как макет таблицы, где информацию можно рассматривать как двумерную матрицу. Он хранится в переменной с именемXи предполагается, что он двумерный с формой [n_samples, n_features]. В основном он содержится в массиве NumPy или DataFrame Pandas. Как было сказано ранее, образцы всегда представляют отдельные объекты, описанные набором данных, а функции представляют собой отдельные наблюдения, которые описывают каждый образец количественным образом.

Данные как целевой массив

Наряду с матрицей функций, обозначенной X, у нас также есть целевой массив. Его еще называют этикеткой. Обозначается y. Метка или целевой массив обычно одномерны и имеют длину n_samples. Обычно он содержится в NumPyarray или панды Series. Целевой массив может иметь как значения, непрерывные числовые значения, так и дискретные значения.

Чем целевой массив отличается от столбцов функций?

Мы можем различить их по одному пункту, что целевой массив обычно является величиной, которую мы хотим предсказать на основе данных, то есть в статистическом плане это зависимая переменная.

пример

В приведенном ниже примере из набора данных ириса мы прогнозируем вид цветка на основе других измерений. В этом случае столбец "Виды" будет рассматриваться как объект.

import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);

Вывод

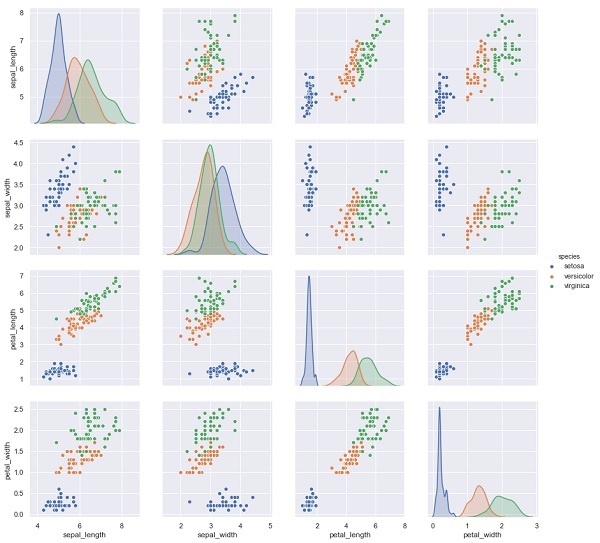
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shape

Вывод

(150,4)
(150,)

В этой главе мы узнаем о Estimator API(интерфейс прикладного программирования). Давайте начнем с понимания, что такое API-интерфейс оценщика.

Что такое API-интерфейс оценщика

Это один из основных API, реализованных Scikit-learn. Он обеспечивает согласованный интерфейс для широкого спектра приложений машинного обучения, поэтому все алгоритмы машинного обучения в Scikit-Learn реализованы через API-интерфейс Estimator. Объект, который учится на данных (соответствует данным), является оценщиком. Его можно использовать с любым из алгоритмов, таких как классификация, регрессия, кластеризация, или даже с преобразователем, который извлекает полезные функции из необработанных данных.

Для подгонки данных все объекты оценщика предоставляют метод подбора, который принимает набор данных, показанный ниже:

estimator.fit(data)

Затем все параметры оценщика могут быть установлены следующим образом, когда он создается соответствующим атрибутом.

estimator = Estimator (param1=1, param2=2)
estimator.param1

Результатом выше будет 1.

После того, как данные подобраны с помощью оценщика, параметры оцениваются на основе имеющихся данных. Теперь все предполагаемые параметры будут атрибутами объекта оценки, оканчивающимися подчеркиванием следующим образом:

estimator.estimated_param_

Использование API-интерфейса оценщика

Основные виды использования оценщиков следующие:

Оценка и расшифровка модели

Объект оценщика используется для оценки и декодирования модели. Кроме того, модель оценивается как детерминированная функция следующего:

• Параметры, предусмотренные при строительстве объекта.

• Глобальное случайное состояние (numpy.random), если для параметра random_state оценщика установлено значение none.

• Любые данные, переданные последнему вызову fit, fit_transform, or fit_predict.

• Любые данные, передаваемые в последовательности обращений к partial_fit.

Отображение непрямоугольного представления данных в прямоугольные данные

Он отображает непрямоугольное представление данных в прямоугольные данные. Проще говоря, он принимает входные данные, где каждый образец не представлен как объект, подобный массиву, фиксированной длины, и создает подобный массиву объект функций для каждого образца.

Различие между керном и удаленными образцами

Он моделирует различие между керном и удаленными образцами, используя следующие методы:

• fit

• fit_predict, если трансдуктивный

• предсказать, если индуктивный

Руководящие принципы

При разработке Scikit-Learn API необходимо учитывать следующие руководящие принципы:

Последовательность

Этот принцип гласит, что все объекты должны иметь общий интерфейс, созданный из ограниченного набора методов. Документация также должна быть согласованной.

Ограниченная иерархия объектов

Этот руководящий принцип гласит:

• Алгоритмы должны быть представлены классами Python

• Наборы данных должны быть представлены в стандартном формате, таком как массивы NumPy, Pandas DataFrames, разреженная матрица SciPy.

• Имена параметров должны использовать стандартные строки Python.

Сочинение

Как мы знаем, алгоритмы машинного обучения можно выразить как последовательность многих фундаментальных алгоритмов. Scikit-learn использует эти фундаментальные алгоритмы всякий раз, когда это необходимо.

Разумные настройки по умолчанию

В соответствии с этим принципом библиотека Scikit-learn определяет соответствующее значение по умолчанию, когда модели машинного обучения требуют параметров, задаваемых пользователем.

Осмотр

В соответствии с этим руководящим принципом каждое указанное значение параметра отображается как публичные атрибуты.

Шаги по использованию API-интерфейса оценщика

Ниже приведены шаги по использованию API оценки Scikit-Learn.

Шаг 1. Выберите класс модели

На этом первом этапе нам нужно выбрать класс модели. Это можно сделать, импортировав соответствующий класс оценщика из Scikit-learn.

Шаг 2: Выберите гиперпараметры модели

На этом этапе нам нужно выбрать гиперпараметры модели класса. Это можно сделать, создав экземпляр класса с желаемыми значениями.

Шаг 3. Упорядочение данных

Затем нам нужно организовать данные в матрицу функций (X) и целевой вектор (y).

Шаг 4: Примерка модели

Теперь нам нужно подогнать модель к вашим данным. Это можно сделать, вызвав метод fit () экземпляра модели.

Шаг 5: Применение модели

После подбора модели мы можем применить ее к новым данным. Для обучения с учителем используйтеpredict()метод прогнозирования меток для неизвестных данных. В то время как для обучения без учителя используйтеpredict() или же transform() для вывода свойств данных.

Пример контролируемого обучения

Здесь, в качестве примера этого процесса, мы используем общий случай подгонки строки к данным (x, y), т.е. simple linear regression.

Во-первых, нам нужно загрузить набор данных, мы используем набор данных iris -

пример

import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape

Вывод

(150, 4)

пример

y_iris = iris['species']
y_iris.shape

Вывод

(150,)

пример

Теперь для этого примера регрессии мы собираемся использовать следующие образцы данных -

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);

Вывод

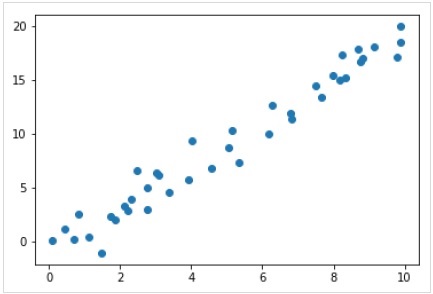
Итак, у нас есть приведенные выше данные для нашего примера линейной регрессии.

Теперь, имея эти данные, мы можем применить вышеупомянутые шаги.

Выберите класс модели

Здесь, чтобы вычислить простую модель линейной регрессии, нам нужно импортировать класс линейной регрессии следующим образом:

from sklearn.linear_model import LinearRegression

Выберите гиперпараметры модели

После того, как мы выбрали класс модели, нам нужно сделать некоторые важные выборы, которые часто представлены как гиперпараметры, или параметры, которые должны быть установлены, прежде чем модель будет соответствовать данным. Здесь, для этого примера линейной регрессии, мы хотели бы подогнать точку пересечения с помощьюfit_intercept гиперпараметр следующим образом -

Example

model = LinearRegression(fit_intercept = True)
model

Output

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)

Организация данных

Теперь, когда мы знаем, что наша целевая переменная y в правильной форме, т.е. длина n_samplesмассив 1-D. Но нам нужно изменить форму матрицы функций.X сделать матрицу размера [n_samples, n_features]. Это можно сделать следующим образом -

Example

X = x[:, np.newaxis]
X.shape

Output

(40, 1)

Подгонка модели

После того, как мы упорядочим данные, пора подобрать модель, то есть применить нашу модель к данным. Это можно сделать с помощьюfit() метод следующим образом -

Example

model.fit(X, y)

Output

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)

В Scikit-learn fit() В конце процесса есть символы подчеркивания.

В этом примере параметр ниже показывает наклон простой линейной аппроксимации данных -

Example

model.coef_

Output

array([1.99839352])

Параметр ниже представляет собой пересечение простого линейного соответствия данным -

Example

model.intercept_

Output

-0.9895459457775022

Применение модели к новым данным

После обучения модели мы можем применить ее к новым данным. Поскольку основной задачей машинного обучения с учителем является оценка модели на основе новых данных, которые не входят в обучающий набор. Это можно сделать с помощьюpredict() метод следующим образом -

Example

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

Output

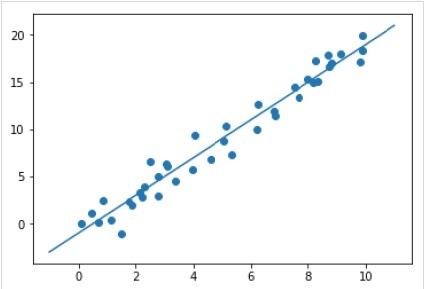
Полный рабочий / исполняемый пример

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape

rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape

model.fit(X, y)
model.coef_
model.intercept_

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

Пример неконтролируемого обучения

Здесь, в качестве примера этого процесса, мы берем общий случай уменьшения размерности набора данных Iris, чтобы его было легче визуализировать. В этом примере мы собираемся использовать анализ главных компонентов (PCA), метод быстрого линейного уменьшения размерности.

Как и в приведенном выше примере, мы можем загрузить и построить случайные данные из набора данных iris. После этого мы можем выполнить следующие шаги:

Выберите класс модели

from sklearn.decomposition import PCA

Выберите гиперпараметры модели

Example

model = PCA(n_components=2)
model

Output

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

Подгонка модели

Example

model.fit(X_iris)

Output

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

Преобразуйте данные в двумерные

Example

X_2D = model.transform(X_iris)

Теперь мы можем построить результат следующим образом -

Output

iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);

Output

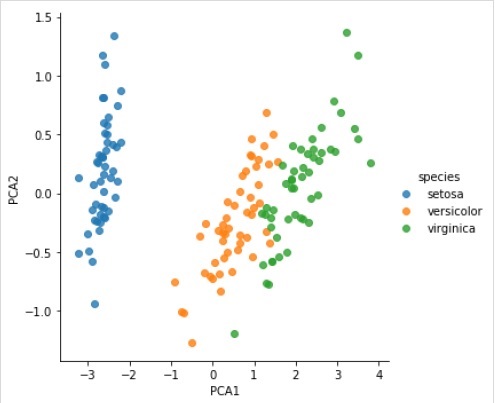
Полный рабочий / исполняемый пример

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA

model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);

Объекты Scikit-learn используют единый базовый API, который состоит из следующих трех дополнительных интерфейсов:

• Estimator interface - Это для сборки и подгонки моделей.

• Predictor interface - Это для прогнозов.

• Transformer interface - Это для преобразования данных.

API-интерфейсы принимают простые соглашения, а выбор дизайна направлен таким образом, чтобы избежать увеличения количества кода фреймворка.

Цель конвенций

Цель соглашений - убедиться, что API придерживается следующих общих принципов:

Consistency - Все объекты, будь то базовые или составные, должны иметь согласованный интерфейс, который в свою очередь состоит из ограниченного набора методов.

Inspection - Параметры конструктора и значения параметров, определенные алгоритмом обучения, должны храниться и отображаться как общедоступные атрибуты.

Non-proliferation of classes - Наборы данных должны быть представлены в виде массивов NumPy или разреженной матрицы Scipy, тогда как имена и значения гиперпараметров должны быть представлены как стандартные строки Python, чтобы избежать распространения кода фреймворка.

Composition - Алгоритмы, независимо от того, выражаются ли они в виде последовательностей или комбинаций преобразований данных или естественно рассматриваются как метаалгоритмы, параметризованные на других алгоритмах, должны быть реализованы и составлены из существующих строительных блоков.

Sensible defaults- В scikit-learn всякий раз, когда для операции требуется пользовательский параметр, определяется соответствующее значение по умолчанию. Это значение по умолчанию должно приводить к разумному выполнению операции, например, давая базовое решение для текущей задачи.

Различные соглашения

Соглашения, доступные в Sklearn, объясняются ниже -

Приведение типов

В нем говорится, что ввод должен быть приведен к float64. В следующем примере, в которомsklearn.random_projection модуль, используемый для уменьшения размерности данных, объяснит это -

Example

import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtype

Output

dtype('float32')
dtype('float64')

В приведенном выше примере мы видим, что X - это float32 который бросается в float64 по fit_transform(X).

Установка и обновление параметров

Гиперпараметры оценщика могут быть обновлены и переустановлены после того, как он был построен с помощью set_params()метод. Давайте посмотрим на следующий пример, чтобы понять это -

Example

import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])

Output

array([0, 0, 0, 0, 0])

После создания оценщика приведенный выше код изменит ядро ​​по умолчанию. rbf линейно через SVC.set_params().

Теперь следующий код изменит ядро ​​обратно на rbf, чтобы переустановить оценщик и сделать второй прогноз.

Example

clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])

Output

array([0, 0, 0, 0, 0])

Полный код

Ниже приводится полная исполняемая программа -

import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])

Примерка Multiclass и Multilabel

В случае подбора мультикласса задачи обучения и прогнозирования зависят от формата целевых данных. Используемый модульsklearn.multiclass. Посмотрите пример ниже, где мультиклассовый классификатор помещается в 1d-массив.

Example

from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)

Output

array([0, 0, 1, 1, 2])

В приведенном выше примере классификатор помещается в одномерный массив меток мультикласса, а predict()Таким образом, метод обеспечивает соответствующее многоклассовое предсказание. Но, с другой стороны, также возможно уместить двумерный массив бинарных индикаторов меток следующим образом:

Example

from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)

Output

array(
   [
      [0, 0, 0],
      [0, 0, 0],
      [0, 1, 0],
      [0, 1, 0],
      [0, 0, 0]
   ]
)

Точно так же в случае установки нескольких меток экземпляру можно присвоить несколько меток следующим образом:

Example

from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)

Output

array(
   [
      [1, 0, 1, 0, 0],
      [1, 0, 1, 0, 0],
      [1, 0, 1, 1, 0],
      [1, 0, 1, 1, 0],
      [1, 0, 1, 0, 0]
   ]
)

В приведенном выше примере sklearn.MultiLabelBinarizerиспользуется для преобразования в двоичную форму двумерного массива мультиэлементов для размещения на нем. Вот почему функция predic () выдает 2d-массив в качестве вывода с несколькими метками для каждого экземпляра.

Эта глава поможет вам узнать о линейном моделировании в Scikit-Learn. Давайте начнем с понимания того, что такое линейная регрессия в Sklearn.

В следующей таблице перечислены различные линейные модели, предоставляемые Scikit-Learn.

Старший Нет	Модель и описание
1	Линейная регрессия Это одна из лучших статистических моделей, изучающая связь между зависимой переменной (Y) с заданным набором независимых переменных (X).
2	Логистическая регрессия Логистическая регрессия, несмотря на свое название, представляет собой алгоритм классификации, а не алгоритм регрессии. На основе заданного набора независимых переменных он используется для оценки дискретного значения (0 или 1, да / нет, истина / ложь).
3	Риджская регрессия Риджерная регрессия или регуляризация Тихонова - это метод регуляризации, который выполняет регуляризацию L2. Он изменяет функцию потерь, добавляя штраф (величина усадки), эквивалентный квадрату величины коэффициентов.
4	Регрессия Байесовского хребта Байесовская регрессия позволяет естественному механизму выжить при недостаточном количестве данных или плохо распределенных данных, формулируя линейную регрессию с использованием распределителей вероятностей, а не точечных оценок.
5	ЛАССО LASSO - это метод регуляризации, который выполняет регуляризацию L1. Он изменяет функцию потерь, добавляя штраф (количество усадки), эквивалентный суммированию абсолютных значений коэффициентов.
6	Многозадачность LASSO Это позволяет согласовывать несколько задач регрессии, одновременно обеспечивая, чтобы выбранные функции были одинаковыми для всех задач регрессии, также называемых задачами. Sklearn предоставляет линейную модель под названием MultiTaskLasso, обученную со смешанной L1, L2-нормой для регуляризации, которая совместно оценивает разреженные коэффициенты для множественных задач регрессии.
7	Эластичная сетка Elastic-Net - это метод регуляризованной регрессии, который линейно комбинирует оба штрафа, то есть L1 и L2 методов регрессии Лассо и Риджа. Это полезно, когда есть несколько коррелированных функций.
8	Многозадачная Elastic-Net Это модель Elastic-Net, которая позволяет решать несколько задач регрессии, совместно применяя выбранные функции, чтобы они были одинаковыми для всех задач регрессии, также называемых задачами.

В этой главе основное внимание уделяется полиномиальным функциям и инструментам конвейерной обработки в Sklearn.

Введение в полиномиальные характеристики

Линейные модели, обученные нелинейным функциям данных, обычно обеспечивают высокую производительность линейных методов. Это также позволяет им обрабатывать гораздо более широкий диапазон данных. Поэтому в машинном обучении используются такие линейные модели, которые обучаются на нелинейных функциях.

Одним из таких примеров является то, что простая линейная регрессия может быть расширена путем построения полиномиальных функций из коэффициентов.

Математически предположим, что у нас есть стандартная модель линейной регрессии, тогда для двухмерных данных это будет выглядеть так:

$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$

Теперь мы можем объединить функции в полиномы второго порядка, и наша модель будет выглядеть следующим образом:

$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$

Вышеупомянутая модель все еще является линейной. Здесь мы увидели, что полученная полиномиальная регрессия относится к тому же классу линейных моделей и может быть решена аналогичным образом.

Для этого scikit-learn предоставляет модуль с именем PolynomialFeatures. Этот модуль преобразует матрицу входных данных в новую матрицу данных заданной степени.

Параметры

В следующей таблице представлены параметры, используемые PolynomialFeatures модуль

Старший Нет	Параметр и описание
1	degree - целое число, по умолчанию = 2 Он представляет собой степень полиномиальных характеристик.
2	interaction_only - Boolean, по умолчанию = false По умолчанию это false, но если установлено как true, создаются функции, которые являются продуктами большей части различных входных функций. Такие функции называются функциями взаимодействия.
3	include_bias - Boolean, по умолчанию = true Он включает столбец смещения, т. Е. Функцию, в которой все степени полиномов равны нулю.
4	order - str in {'C', 'F'}, по умолчанию = 'C' Этот параметр представляет порядок вывода массива в плотном случае. Порядок «F» означает более быстрое вычисление, но, с другой стороны, он может замедлить последующие оценки.

Атрибуты

Следующая таблица содержит атрибуты, используемые PolynomialFeatures модуль

Старший Нет	Атрибуты и описание
1	powers_ - массив, форма (n_output_features, n_input_features) Он показывает, что powers_ [i, j] - это показатель степени j-го входа в i-м выходе.
2	n_input_features _ - int Как следует из названия, он дает общее количество входных функций.
3	n_output_features _ - int Как следует из названия, он дает общее количество полиномиальных выходных функций.

Пример реализации

Следующий скрипт Python использует PolynomialFeatures трансформатор для преобразования массива из 8 в форму (4,2) -

from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)

Вывод

array(
   [
      [ 1., 0., 1., 0., 0., 1.],
      [ 1., 2., 3., 4., 6., 9.],
      [ 1., 4., 5., 16., 20., 25.],
      [ 1., 6., 7., 36., 42., 49.]
   ]
)

Оптимизация с помощью инструментов конвейера

Вышеупомянутый вид предварительной обработки, то есть преобразование матрицы входных данных в новую матрицу данных заданной степени, может быть оптимизирован с помощью Pipeline инструменты, которые в основном используются для объединения нескольких оценщиков в одну.

пример

Приведенные ниже сценарии python с использованием инструментов Scikit-learn Pipeline для оптимизации предварительной обработки (будут соответствовать полиномиальным данным третьего порядка).

#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np

#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])

#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)

#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_

Вывод

array([ 3., -2., 1., -1.])

Приведенные выше выходные данные показывают, что линейная модель, обученная полиномиальным признакам, способна восстановить точные входные коэффициенты полинома.

Здесь мы узнаем об алгоритме оптимизации в Sklearn, называемом стохастическим градиентным спуском (SGD).

Стохастический градиентный спуск (SGD) - это простой, но эффективный алгоритм оптимизации, используемый для поиска значений параметров / коэффициентов функций, которые минимизируют функцию стоимости. Другими словами, он используется для дискриминативного обучения линейных классификаторов при выпуклых функциях потерь, таких как SVM и логистическая регрессия. Он был успешно применен к крупномасштабным наборам данных, поскольку обновление коэффициентов выполняется для каждого обучающего экземпляра, а не в конце экземпляров.

Классификатор SGD

Классификатор стохастического градиентного спуска (SGD) в основном реализует простую процедуру обучения SGD, поддерживающую различные функции потерь и штрафы за классификацию. Scikit-learn предоставляетSGDClassifier модуль для реализации классификации SGD.

Параметры

В следующей таблице представлены параметры, используемые SGDClassifier модуль -

Старший Нет	Параметр и описание
1	loss - str, по умолчанию = 'шарнир' Он представляет функцию потерь, которая будет использоваться при реализации. Значение по умолчанию - «шарнир», что даст нам линейную SVM. Другие варианты, которые можно использовать: log - Эта потеря даст нам логистическую регрессию, то есть вероятностный классификатор. modified_huber - плавная потеря, которая вносит терпимость к выбросам вместе с оценками вероятности. squared_hinge - аналогично потере петли, но штрафуется квадратично. perceptron - как следует из названия, алгоритм перцептрона использует линейные потери.
2	penalty - str, 'none', 'l2', 'l1', 'elasticnet' Это термин регуляризации, используемый в модели. По умолчанию это L2. Мы можем использовать L1 или 'elasticnet; также, но оба могут сделать модель разреженной, что недостижимо с L2.
3	alpha - float, по умолчанию = 0,0001 Альфа, константа, которая умножает член регуляризации, является параметром настройки, который определяет, насколько мы хотим наказать модель. Значение по умолчанию - 0,0001.
4	l1_ratio - float, по умолчанию = 0,15 Это называется параметром смешивания ElasticNet. Его диапазон: 0 <= l1_ratio <= 1. Если l1_ratio = 1, штраф будет L1. Если l1_ratio = 0, штраф будет штрафом L2.
5	fit_intercept - Boolean, по умолчанию = True Этот параметр указывает, что к функции принятия решения должна быть добавлена ​​константа (смещение или перехват). В расчетах не будет использоваться перехват, и данные будут считаться уже центрированными, если для него будет установлено значение false.
6	tol - float или none, необязательно, по умолчанию = 1.e-3 Этот параметр представляет собой критерий остановки для итераций. Его значение по умолчанию - False, но если установлено None, итерации остановятся, когдаloss > best_loss - tol for n_iter_no_changeсменяющие друг друга эпохи.
7	shuffle - Логическое значение, необязательно, по умолчанию = True Этот параметр указывает, хотим ли мы, чтобы наши обучающие данные перетасовывались после каждой эпохи или нет.
8	verbose - целое число, по умолчанию = 0 Он представляет уровень детализации. Его значение по умолчанию - 0.
9	epsilon - float, по умолчанию = 0,1 Этот параметр указывает ширину нечувствительной области. Если потеря = 'epsilon-нечувствительность', любая разница между текущим предсказанием и правильной меткой, меньше порогового значения, будет игнорироваться.
10	max_iter - int, необязательно, по умолчанию = 1000 Как следует из названия, он представляет максимальное количество проходов за эпохи, т.е. данные обучения.
11	warm_start - bool, необязательно, по умолчанию = false Если для этого параметра установлено значение True, мы можем повторно использовать решение предыдущего вызова, чтобы оно соответствовало инициализации. Если мы выберем default, то есть false, предыдущее решение будет удалено.
12	random_state - int, экземпляр RandomState или None, необязательно, по умолчанию = none Этот параметр представляет собой начальное число сгенерированного псевдослучайного числа, которое используется при перетасовке данных. Следующие варианты. int - В этом случае random_state это начальное число, используемое генератором случайных чисел. RandomState instance - В этом случае random_state - генератор случайных чисел. None - В этом случае генератор случайных чисел - это экземпляр RandonState, используемый np.random.
13	n_jobs - int или none, необязательно, по умолчанию = None Он представляет собой количество процессоров, которые будут использоваться в вычислениях OVA (один против всех) для задач с несколькими классами. Значение по умолчанию - none, что означает 1.
14	learning_rate - строка, необязательный, по умолчанию = 'оптимальный' Если скорость обучения «постоянная», eta = eta0; Если скорость обучения «оптимальная», eta = 1.0 / (alpha * (t + t0)), где t0 выбрано Леоном Ботто; Если скорость обучения = 'invscalling', eta = eta0 / pow (t, power_t). Если скорость обучения = «адаптивная», eta = eta0.
15	eta0 - двойной, по умолчанию = 0,0 Он представляет собой начальную скорость обучения для вышеупомянутых вариантов скорости обучения, то есть «постоянный», «invscalling» или «адаптивный».
16	power_t - idouble, по умолчанию = 0,5 Это показатель «ускоряющейся» скорости обучения.
17	early_stopping - bool, по умолчанию = False Этот параметр представляет использование ранней остановки для завершения обучения, когда оценка валидации не улучшается. Его значение по умолчанию - false, но если установлено значение true, оно автоматически откладывает стратифицированную часть обучающих данных как проверку и останавливает обучение, когда оценка проверки не улучшается.
18	validation_fraction - float, по умолчанию = 0,1 Он используется только тогда, когда Early_stopping истинно. Он представляет собой долю обучающих данных, которую нужно отложить в качестве набора для проверки для досрочного завершения обучающих данных.
19	n_iter_no_change - int, по умолчанию = 5 Он представляет собой количество итераций без каких-либо улучшений, если алгоритм будет запущен до ранней остановки.
20	classs_weight - dict, {class_label: weight} или «сбалансированный», или None, необязательно Этот параметр представляет веса, связанные с классами. Если не указано иное, классы должны иметь вес 1.
20	warm_start - bool, необязательно, по умолчанию = false Если для этого параметра установлено значение True, мы можем повторно использовать решение предыдущего вызова, чтобы оно соответствовало инициализации. Если мы выберем default, то есть false, предыдущее решение будет удалено.
21 год	average - iBoolean или int, необязательно, по умолчанию = false Он представляет собой количество процессоров, которые будут использоваться в вычислениях OVA (один против всех) для задач с несколькими классами. Значение по умолчанию - none, что означает 1.

Атрибуты

В следующей таблице представлены атрибуты, используемые SGDClassifier модуль -

Старший Нет	Атрибуты и описание
1	coef_ - массив, форма (1, n_features), если n_classes == 2, else (n_classes, n_features) Этот атрибут обеспечивает вес, присвоенный функциям.
2	intercept_ - массив, shape (1,) if n_classes == 2, else (n_classes,) Он представляет собой независимый член в функции принятия решения.
3	n_iter_ - int Он дает количество итераций для достижения критерия остановки.

Implementation Example

Как и другие классификаторы, стохастический градиентный спуск (SGD) должен быть оснащен следующими двумя массивами:

• Массив X, содержащий обучающие образцы. Он имеет размер [n_samples, n_features].

• Массив Y, содержащий целевые значения, т.е. метки классов для обучающих выборок. Его размер [n_samples].

Example

Следующий скрипт Python использует линейную модель SGDClassifier -

import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)

Output

SGDClassifier(
   alpha = 0.0001, average = False, class_weight = None,
   early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
   l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
   n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
   power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
   validation_fraction = 0.1, verbose = 0, warm_start = False
)

Example

Теперь, после подбора, модель может предсказывать новые значения следующим образом:

SGDClf.predict([[2.,2.]])

Output

array([2])

Example

В приведенном выше примере мы можем получить вектор веса с помощью следующего скрипта Python:

SGDClf.coef_

Output

array([[19.54811198, 9.77200712]])

Example

Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -

SGDClf.intercept_

Output

array([10.])

Example

Мы можем получить расстояние со знаком до гиперплоскости, используя SGDClassifier.decision_function как используется в следующем скрипте Python -

SGDClf.decision_function([[2., 2.]])

Output

array([68.6402382])

Регрессор SGD

Регрессор стохастического градиентного спуска (SGD) в основном реализует простую процедуру обучения SGD, поддерживающую различные функции потерь и штрафы для соответствия моделям линейной регрессии. Scikit-learn предоставляетSGDRegressor модуль для реализации регрессии SGD.

Параметры

Параметры, используемые SGDRegressorпочти такие же, как и в модуле SGDClassifier. Отличие заключается в параметре «убыток». ЗаSGDRegressor Параметр потерь модулей положительные значения следующие:

• squared_loss - Относится к обычному методу наименьших квадратов.

• huber: SGDRegressor- исправить выбросы, переключившись с квадратов на линейные потери на расстоянии эпсилон. Работа huber заключается в том, чтобы изменить squared_loss, чтобы алгоритм меньше фокусировался на исправлении выбросов.

• epsilon_insensitive - На самом деле он игнорирует ошибки меньше, чем epsilon.

• squared_epsilon_insensitive- То же, что и epsilon_insensitive. Единственная разница в том, что это становится квадратом потерь сверх допуска эпсилон.

Еще одно отличие состоит в том, что параметр power_t имеет значение по умолчанию 0,25, а не 0,5, как в SGDClassifier. Кроме того, у него нет параметров class_weight и n_jobs.

Атрибуты

Атрибуты SGDRegressor такие же, как и у модуля SGDClassifier. Скорее у него есть три дополнительных атрибута, а именно:

• average_coef_ - массив, форма (n_features,)

Как следует из названия, он предоставляет средние веса, присвоенные функциям.

• average_intercept_ - массив, форма (1,)

Как следует из названия, он обеспечивает усредненный член перехвата.

• t_ - int

Он предоставляет количество обновлений веса, выполненных во время фазы тренировки.

Note - атрибуты average_coef_ и average_intercept_ будут работать после включения параметра «средний» в значение True.

Implementation Example

Следующий скрипт Python использует SGDRegressor линейная модель -

import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
   max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)

Output

SGDRegressor(
   alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
   eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
   learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
   n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
   random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
   verbose = 0, warm_start = False
)

Example

Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -

SGDReg.coef_

Output

array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])

Example

Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -

SGReg.intercept_

Output

SGReg.intercept_

Example

Мы можем получить количество обновлений веса во время фазы тренировки с помощью следующего скрипта Python:

SGDReg.t_

Output

61.0

Плюсы и минусы SGD

Следуя за плюсами SGD -

• Стохастический градиентный спуск (SGD) очень эффективен.

• Это очень легко реализовать, так как есть много возможностей для настройки кода.

После минусов SGD -

• Для стохастического градиентного спуска (SGD) требуется несколько гиперпараметров, таких как параметры регуляризации.

• Он чувствителен к масштабированию функции.

В этой главе рассматривается метод машинного обучения, называемый машинами опорных векторов (SVM).

Введение

Машины опорных векторов (SVM) - это мощные, но гибкие методы контролируемого машинного обучения, используемые для классификации, регрессии и обнаружения выбросов. SVM очень эффективны в пространствах большой размерности и обычно используются в задачах классификации. SVM популярны и эффективны с точки зрения памяти, потому что они используют подмножество обучающих точек в функции принятия решения.

Основная цель SVM - разделить наборы данных на несколько классов, чтобы найти maximum marginal hyperplane (MMH) что можно сделать в следующие два шага -

• Машины опорных векторов сначала будут генерировать гиперплоскости итеративно, что наилучшим образом разделяет классы.

• После этого он выберет гиперплоскость, которая правильно разделяет классы.

Некоторые важные концепции в SVM следующие:

• Support Vectors- Их можно определить как точки данных, которые находятся ближе всего к гиперплоскости. Опорные векторы помогают определить разделительную линию.

• Hyperplane - Плоскость решения или пространство, разделяющее множество объектов разных классов.

• Margin - Промежуток между двумя линиями на контрольных точках шкафа разных классов называется маржей.

Следующие диаграммы дадут вам представление об этих концепциях SVM.

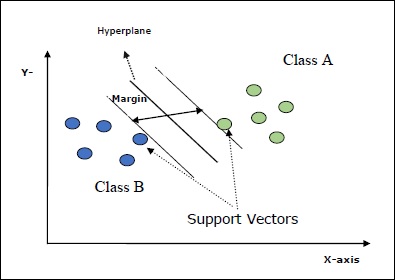
SVM в Scikit-learn поддерживает в качестве входных данных как разреженные, так и плотные выборочные векторы.

Классификация SVM

Scikit-learn предоставляет три класса, а именно: SVC, NuSVC и LinearSVC который может выполнять классификацию мультиклассов.

SVC

Это классификация C-опорных векторов, реализация которой основана на libsvm. Модуль, используемый scikit-learn:sklearn.svm.SVC. Этот класс обрабатывает поддержку мультикласса по схеме «один против одного».

Параметры

В следующей таблице представлены параметры, используемые sklearn.svm.SVC класс -

Старший Нет	Параметр и описание
1	C - float, необязательно, по умолчанию = 1.0 Это штрафной параметр члена ошибки.
2	kernel - строка, необязательно, по умолчанию = 'rbf' Этот параметр указывает тип ядра, которое будет использоваться в алгоритме. мы можем выбрать любой среди,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. Значение ядра по умолчанию будет‘rbf’.
3	degree - int, необязательно, по умолчанию = 3 Он представляет собой степень функции ядра «poly» и будет игнорироваться всеми другими ядрами.
4	gamma - {'scale', 'auto'} или float, Это коэффициент ядра для ядер "rbf", "poly" и "sigmoid".
5	optinal default - = 'масштаб' Если вы выберете значение по умолчанию, то есть gamma = 'scale', тогда значение гаммы, которое будет использоваться SVC, будет 1 / (_ ∗. ()). С другой стороны, если gamma = 'auto', используется 1 / _.
6	coef0 - float, необязательно, по умолчанию = 0,0 Независимый термин в функции ядра, который имеет значение только в 'poly' и 'sigmoid'.
7	tol - float, необязательно, по умолчанию = 1.e-3 Этот параметр представляет собой критерий остановки для итераций.
8	shrinking - Логическое значение, необязательно, по умолчанию = True Этот параметр указывает, хотим ли мы использовать эвристику сжатия или нет.
9	verbose - Boolean, по умолчанию: false Он включает или отключает подробный вывод. Его значение по умолчанию - false.
10	probability - логическое, необязательное, по умолчанию = true Этот параметр включает или отключает оценки вероятности. Значение по умолчанию - false, но оно должно быть включено перед вызовом fit.
11	max_iter - int, необязательно, по умолчанию = -1 Как следует из названия, он представляет собой максимальное количество итераций в решателе. Значение -1 означает, что ограничение на количество итераций отсутствует.
12	cache_size - поплавок, необязательно Этот параметр укажет размер кеша ядра. Значение будет в МБ (мегабайтах).
13	random_state - int, экземпляр RandomState или None, необязательно, по умолчанию = none Этот параметр представляет собой начальное число сгенерированного псевдослучайного числа, которое используется при перетасовке данных. Следующие варианты - int- В этом случае random_state - это начальное число, используемое генератором случайных чисел. RandomState instance - В этом случае random_state - это генератор случайных чисел. None - В этом случае генератор случайных чисел - это экземпляр RandonState, используемый np.random.
14	class_weight - {dict, 'balance'}, необязательно Этот параметр устанавливает для параметра C класса j значение _ℎ [] ∗ для SVC. Если мы используем вариант по умолчанию, это означает, что все классы должны иметь единичный вес. С другой стороны, если вы выберетеclass_weight:balanced, он будет использовать значения y для автоматической настройки весов.
15	decision_function_shape - ovo ',' ovr ', по умолчанию =' ovr ' Этот параметр решает, вернет ли алгоритм ‘ovr’ (one-vs-rest) решающая функция формы, как и все другие классификаторы, или исходная ovo(один против одного) решающая функция libsvm.
16	break_ties - логическое, необязательное, по умолчанию = false True - Прогноз разорвет связи в соответствии со значениями достоверности solution_function False - Прогноз вернет первый класс среди связанных классов.

Атрибуты

Следующая таблица содержит атрибуты, используемые sklearn.svm.SVC класс -

Старший Нет	Атрибуты и описание
1	support_ - в виде массива, shape = [n_SV] Возвращает индексы опорных векторов.
2	support_vectors_ - в виде массива, shape = [n_SV, n_features] Он возвращает опорные векторы.
3	n_support_ - как массив, dtype = int32, shape = [n_class] Он представляет количество опорных векторов для каждого класса.
4	dual_coef_ - массив, shape = [n_class-1, n_SV] Это коэффициенты опорных векторов в решающей функции.
5	coef_ - массив, shape = [n_class * (n_class-1) / 2, n_features] Этот атрибут, доступный только в случае линейного ядра, обеспечивает вес, присвоенный функциям.
6	intercept_ - массив, форма = [n_class * (n_class-1) / 2] Он представляет собой независимый член (константу) в решающей функции.
7	fit_status_ - int Если он установлен правильно, то на выходе будет 0. Если он установлен неправильно, выход будет 1.
8	classes_ - массив формы = [n_classes] Он дает метки классов.

Implementation Example

Как и другие классификаторы, SVC также должен быть оснащен следующими двумя массивами:

• Массив Xпроведение обучающих выборок. Он имеет размер [n_samples, n_features].

• Массив Yудерживание целевых значений, то есть меток классов для обучающих выборок. Его размер [n_samples].

Следующий скрипт Python использует sklearn.svm.SVC класс -

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)

Output

SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, probability = False, random_state = None, shrinking = False,
   tol = 0.001, verbose = False)

Example

Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -

SVCClf.coef_

Output

array([[0.5, 0.5]])

Example

Точно так же мы можем получить значение других атрибутов следующим образом:

SVCClf.predict([[-0.5,-0.8]])

Output

array([1])

Example

SVCClf.n_support_

Output

array([1, 1])

Example

SVCClf.support_vectors_

Output

array(
   [
      [-1., -1.],
      [ 1., 1.]
   ]
)

Example

SVCClf.support_

Output

array([0, 2])

Example

SVCClf.intercept_

Output

array([-0.])

Example

SVCClf.fit_status_

Output

0

NuSVC

NuSVC - это классификация опорных векторов Nu. Это еще один класс, предоставляемый scikit-learn, который может выполнять мультиклассовую классификацию. Это похоже на SVC, но NuSVC принимает несколько другие наборы параметров. Параметр, который отличается от SVC, выглядит следующим образом -

• nu - float, необязательно, по умолчанию = 0.5

Он представляет собой верхнюю границу доли ошибок обучения и нижнюю границу доли опорных векторов. Его значение должно быть в интервале (o, 1].

Остальные параметры и атрибуты такие же, как у SVC.

Пример реализации

Мы можем реализовать тот же пример, используя sklearn.svm.NuSVC класс тоже.

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)

Вывод

NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, nu = 0.5, probability = False, random_state = None,
   shrinking = False, tol = 0.001, verbose = False)

Мы можем получить выходные данные остальных атрибутов, как это было в случае с SVC.

LinearSVC

Это классификация линейных опорных векторов. Это похоже на SVC с ядром = 'linear'. Разница между ними в том, чтоLinearSVC реализован в терминах liblinear, в то время как SVC реализован в libsvm. Вот в чем причинаLinearSVCимеет большую гибкость в выборе функций штрафов и потерь. Он также лучше масштабируется для большого количества выборок.

Если говорить о его параметрах и атрибутах, то он не поддерживает ‘kernel’ поскольку предполагается, что он линейный, и ему также не хватает некоторых атрибутов, таких как support_, support_vectors_, n_support_, fit_status_ и, dual_coef_.

Однако он поддерживает penalty и loss параметры следующим образом -

• penalty − string, L1 or L2(default = ‘L2’)

  Этот параметр используется для указания нормы (L1 или L2), используемой при пенализации (регуляризации).

• loss − string, hinge, squared_hinge (default = squared_hinge)

  Он представляет функцию потерь, где «шарнир» - это стандартные потери SVM, а «квадрат_холоста» - квадрат потерь в шарнире.

Пример реализации

Следующий скрипт Python использует sklearn.svm.LinearSVC класс -

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)

Вывод

LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
   intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
   multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)

пример

Теперь, после подбора, модель может предсказывать новые значения следующим образом:

LSVCClf.predict([[0,0,0,0]])

Вывод

[1]

пример

В приведенном выше примере мы можем получить вектор веса с помощью следующего скрипта Python:

LSVCClf.coef_

Вывод

[[0. 0. 0.91214955 0.22630686]]

пример

Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -

LSVCClf.intercept_

Вывод

[0.26860518]

Регрессия с SVM

Как обсуждалось ранее, SVM используется как для задач классификации, так и для решения задач регрессии. Метод классификации опорных векторов (SVC) Scikit-learn также может быть расширен для решения задач регрессии. Этот расширенный метод называется регрессией опорных векторов (SVR).

Основное сходство между SVM и SVR

Модель, созданная SVC, зависит только от подмножества обучающих данных. Почему? Потому что функция затрат для построения модели не заботится о точках обучающих данных, которые лежат за пределами поля.

Принимая во внимание, что модель, созданная SVR (регрессия опорных векторов), также зависит только от подмножества обучающих данных. Почему? Поскольку функция стоимости для построения модели игнорирует любые точки обучающих данных, близкие к предсказанию модели.

Scikit-learn предоставляет три класса, а именно: SVR, NuSVR and LinearSVR как три разные реализации SVR.

СВР

Это векторная регрессия с поддержкой Epsilon, реализация которой основана на libsvm. В отличие отSVC В модели есть два свободных параметра, а именно ‘C’ и ‘epsilon’.

• epsilon - float, необязательно, по умолчанию = 0,1

Он представляет собой эпсилон в модели эпсилон-SVR и определяет эпсилон-трубку, в которой в функции потерь при обучении не связано никаких штрафов с точками, предсказанными в пределах эпсилон-расстояния от фактического значения.

Остальные параметры и атрибуты аналогичны тем, которые мы использовали в SVC.

Пример реализации

Следующий скрипт Python использует sklearn.svm.SVR класс -

from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)

Вывод

SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
   kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)

пример

Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -

SVRReg.coef_

Вывод

array([[0.4, 0.4]])

пример

Точно так же мы можем получить значение других атрибутов следующим образом:

SVRReg.predict([[1,1]])

Вывод

array([1.1])

Точно так же мы можем получить значения других атрибутов.

NuSVR

NuSVR является Nu Support Vector регрессия. Это похоже на NuSVC, но NuSVR использует параметрnuдля контроля количества опорных векторов. Причем, в отличие от NuSVC, гдеnu заменен параметр C, здесь он заменяет epsilon.

Пример реализации

Следующий скрипт Python использует sklearn.svm.SVR класс -

from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)

Вывод

NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
   kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
   verbose = False)

пример

Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -

NuSVRReg.coef_

Вывод

array(
   [
      [-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
      0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
      -0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
   ]
)

Точно так же мы можем получить значение других атрибутов.

LinearSVR

Это линейная регрессия опорных векторов. Это похоже на SVR с ядром = 'linear'. Разница между ними в том, чтоLinearSVR реализовано с точки зрения liblinear, а SVC реализован в libsvm. Вот в чем причинаLinearSVRимеет большую гибкость в выборе функций штрафов и потерь. Он также лучше масштабируется для большого количества выборок.

Если говорить о его параметрах и атрибутах, то он не поддерживает ‘kernel’ поскольку предполагается, что он линейный, и ему также не хватает некоторых атрибутов, таких как support_, support_vectors_, n_support_, fit_status_ и, dual_coef_.

Однако он поддерживает следующие параметры «потери»:

• loss - строка, необязательно, по умолчанию = 'epsilon_insensitive'

Он представляет функцию потерь, где epsilon_insensitive loss - это потеря L1, а квадратичная потеря нечувствительности к epsilon - это потеря L2.

Пример реализации

Следующий скрипт Python использует sklearn.svm.LinearSVR класс -

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)

Вывод

LinearSVR(
   C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
   intercept_scaling=1.0, loss='squared_epsilon_insensitive',
   max_iter=1000, random_state=0, tol=1e-05, verbose=0
)

пример

Теперь, после подбора, модель может предсказывать новые значения следующим образом:

LSRReg.predict([[0,0,0,0]])

Вывод

array([-0.01041416])

пример

В приведенном выше примере мы можем получить вектор веса с помощью следующего скрипта Python:

LSRReg.coef_

Вывод

array([20.47354746, 34.08619401, 67.23189022, 87.47017787])

пример

Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -

LSRReg.intercept_

Вывод

array([-0.01041416])

Здесь мы узнаем о том, что такое обнаружение аномалий в Sklearn и как оно используется для идентификации точек данных.

Обнаружение аномалий - это метод, используемый для определения точек данных в наборе данных, которые не соответствуют остальным данным. Он имеет множество приложений в бизнесе, таких как обнаружение мошенничества, обнаружение вторжений, мониторинг состояния системы, наблюдение и профилактическое обслуживание. Аномалии, которые также называют выбросами, можно разделить на следующие три категории:

• Point anomalies - Это происходит, когда отдельный экземпляр данных считается аномальным по отношению к остальным данным.

• Contextual anomalies- Такая аномалия зависит от контекста. Это происходит, если экземпляр данных является аномальным в определенном контексте.

• Collective anomalies - Это происходит, когда набор связанных экземпляров данных является аномальным в отношении всего набора данных, а не отдельных значений.

Методы

Два метода, а именно outlier detection и novelty detectionможет использоваться для обнаружения аномалий. Необходимо видеть разницу между ними.

Обнаружение выбросов

Данные обучения содержат выбросы, которые далеки от остальных данных. Такие выбросы определяются как наблюдения. По этой причине оценщики обнаружения выбросов всегда стараются соответствовать области с наиболее концентрированными обучающими данными, игнорируя отклоняющиеся наблюдения. Это также известно как неконтролируемое обнаружение аномалий.

Обнаружение новинок

Он связан с обнаружением ненаблюдаемого паттерна в новых наблюдениях, который не включается в обучающие данные. Здесь данные обучения не загрязнены выбросами. Это также известно как полу-контролируемое обнаружение аномалий.

Scikit-learn предоставляет набор инструментов машинного обучения, которые можно использовать как для обнаружения выбросов, так и для обнаружения новинок. Эти инструменты сначала реализуют объектное обучение на основе данных без присмотра с использованием метода fit () следующим образом:

estimator.fit(X_train)

Теперь новые наблюдения будут отсортированы как inliers (labeled 1) или же outliers (labeled -1) используя метод predic () следующим образом -

estimator.fit(X_test)

Оценщик сначала вычислит функцию необработанной оценки, а затем метод прогнозирования будет использовать пороговое значение для этой функции оценки. Мы можем получить доступ к этой необработанной функции оценки с помощьюscore_sample метод и может контролировать порог с помощью contamination параметр.

Мы также можем определить decision_function метод, который определяет выбросы как отрицательное значение, а выбросы как неотрицательное значение.

estimator.decision_function(X_test)

Алгоритмы Sklearn для обнаружения выбросов

Начнем с понимания, что такое эллиптическая оболочка.

Установка эллиптического конверта

Этот алгоритм предполагает, что обычные данные поступают из известного распределения, такого как распределение Гаусса. Для обнаружения выбросов Scikit-learn предоставляет объект с именемcovariance.EllipticEnvelop.

Этот объект соответствует надежной оценке ковариации для данных и, таким образом, соответствует эллипсу центральным точкам данных. Он игнорирует точки за пределами центрального режима.

Параметры

В следующей таблице представлены параметры, используемые sklearn. covariance.EllipticEnvelop метод -

Старший Нет	Параметр и описание
1	store_precision - Логическое значение, необязательно, по умолчанию = True Мы можем указать его, если сохранена предполагаемая точность.
2	assume_centered - Логическое значение, необязательно, по умолчанию = False Если мы установим его в False, он будет вычислять устойчивое местоположение и ковариацию напрямую с помощью алгоритма FastMCD. С другой стороны, если установлено True, будет вычислена поддержка надежного местоположения и ковариантности.
3	support_fraction - float in (0., 1.), необязательно, по умолчанию = None Этот параметр сообщает методу, какая доля точек должна быть включена в поддержку необработанных оценок MCD.
4	contamination - float in (0., 1.), необязательно, по умолчанию = 0.1 Он показывает долю выбросов в наборе данных.
5	random_state - int, экземпляр RandomState или None, необязательно, по умолчанию = none Этот параметр представляет собой начальное число сгенерированного псевдослучайного числа, которое используется при перетасовке данных. Следующие варианты - int - В этом случае random_state это начальное число, используемое генератором случайных чисел. RandomState instance- В этом случае random_state - это генератор случайных чисел. None − In this case, the random number generator is the RandonState instance used by np.random.

Attributes

Following table consist the attributes used by sklearn. covariance.EllipticEnvelop method −

Sr.No	Attributes & Description
1	support_ − array-like, shape(n_samples,) It represents the mask of the observations used to compute robust estimates of location and shape.
2	location_ − array-like, shape (n_features) It returns the estimated robust location.
3	covariance_ − array-like, shape (n_features, n_features) It returns the estimated robust covariance matrix.
4	precision_ − array-like, shape (n_features, n_features) It returns the estimated pseudo inverse matrix.
5	offset_ − float It is used to define the decision function from the raw scores. decision_function = score_samples -offset_

Implementation Example

import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])

Output

array([ 1, -1])

Isolation Forest

In case of high-dimensional dataset, one efficient way for outlier detection is to use random forests. The scikit-learn provides ensemble.IsolationForest method that isolates the observations by randomly selecting a feature. Afterwards, it randomly selects a value between the maximum and minimum values of the selected features.

Here, the number of splitting needed to isolate a sample is equivalent to path length from the root node to the terminating node.

Parameters

Followings table consist the parameters used by sklearn. ensemble.IsolationForest method −

Sr.No	Parameter & Description
1	n_estimators − int, optional, default = 100 It represents the number of base estimators in the ensemble.
2	max_samples − int or float, optional, default = “auto” It represents the number of samples to be drawn from X to train each base estimator. If we choose int as its value, it will draw max_samples samples. If we choose float as its value, it will draw max_samples ∗ .shape[0] samples. And, if we choose auto as its value, it will draw max_samples = min(256,n_samples).
3	support_fraction − float in (0., 1.), optional, default = None This parameter tells the method that how much proportion of points to be included in the support of the raw MCD estimates.
4	contamination − auto or float, optional, default = auto It provides the proportion of the outliers in the data set. If we set it default i.e. auto, it will determine the threshold as in the original paper. If set to float, the range of contamination will be in the range of [0,0.5].
5	random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options − int − In this case, random_state is the seed used by random number generator. RandomState instance − In this case, random_state is the random number generator. None − In this case, the random number generator is the RandonState instance used by np.random.
6	max_features − int or float, optional (default = 1.0) It represents the number of features to be drawn from X to train each base estimator. If we choose int as its value, it will draw max_features features. If we choose float as its value, it will draw max_features * X.shape[] samples.
7	bootstrap − Boolean, optional (default = False) Its default option is False which means the sampling would be performed without replacement. And on the other hand, if set to True, means individual trees are fit on a random subset of the training data sampled with replacement.
8	n_jobs − int or None, optional (default = None) It represents the number of jobs to be run in parallel for fit() and predict() methods both.
9	verbose − int, optional (default = 0) This parameter controls the verbosity of the tree building process.
10	warm_start − Bool, optional (default=False) If warm_start = true, we can reuse previous calls solution to fit and can add more estimators to the ensemble. But if is set to false, we need to fit a whole new forest.

Attributes

Following table consist the attributes used by sklearn. ensemble.IsolationForest method −

Sr.No	Attributes & Description
1	estimators_ − list of DecisionTreeClassifier Providing the collection of all fitted sub-estimators.
2	max_samples_ − integer It provides the actual number of samples used.
3	offset_ − float It is used to define the decision function from the raw scores. decision_function = score_samples -offset_

Implementation Example

The Python script below will use sklearn. ensemble.IsolationForest method to fit 10 trees on given data

from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)

Output

IsolationForest(
   behaviour = 'old', bootstrap = False, contamination='legacy',
   max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
   random_state = None, verbose = 0
)

Local Outlier Factor

Local Outlier Factor (LOF) algorithm is another efficient algorithm to perform outlier detection on high dimension data. The scikit-learn provides neighbors.LocalOutlierFactor method that computes a score, called local outlier factor, reflecting the degree of anomality of the observations. The main logic of this algorithm is to detect the samples that have a substantially lower density than its neighbors. Thats why it measures the local density deviation of given data points w.r.t. their neighbors.

Parameters

Followings table consist the parameters used by sklearn. neighbors.LocalOutlierFactor method

Sr.No	Parameter & Description
1	n_neighbors − int, optional, default = 20 It represents the number of neighbors use by default for kneighbors query. All samples would be used if .
2	algorithm − optional Which algorithm to be used for computing nearest neighbors. If you choose ball_tree, it will use BallTree algorithm. If you choose kd_tree, it will use KDTree algorithm. If you choose brute, it will use brute-force search algorithm. If you choose auto, it will decide the most appropriate algorithm on the basis of the value we passed to fit() method.
3	leaf_size − int, optional, default = 30 The value of this parameter can affect the speed of the construction and query. It also affects the memory required to store the tree. This parameter is passed to BallTree or KdTree algorithms.
4	contamination − auto or float, optional, default = auto It provides the proportion of the outliers in the data set. If we set it default i.e. auto, it will determine the threshold as in the original paper. If set to float, the range of contamination will be in the range of [0,0.5].
5	metric − string or callable, default It represents the metric used for distance computation.
6	P − int, optional (default = 2) It is the parameter for the Minkowski metric. P=1 is equivalent to using manhattan_distance i.e. L1, whereas P=2 is equivalent to using euclidean_distance i.e. L2.
7	novelty − Boolean, (default = False) By default, LOF algorithm is used for outlier detection but it can be used for novelty detection if we set novelty = true.
8	n_jobs − int or None, optional (default = None) It represents the number of jobs to be run in parallel for fit() and predict() methods both.

Attributes

Following table consist the attributes used by sklearn.neighbors.LocalOutlierFactor method −

Sr.No	Attributes & Description
1	negative_outlier_factor_ − numpy array, shape(n_samples,) Providing opposite LOF of the training samples.
2	n_neighbors_ − integer It provides the actual number of neighbors used for neighbors queries.
3	offset_ − float It is used to define the binary labels from the raw scores.

Implementation Example

The Python script given below will use sklearn.neighbors.LocalOutlierFactor method to construct NeighborsClassifier class from any array corresponding our data set

from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)

Output

NearestNeighbors(
   algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
   metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)

Example

Now, we can ask from this constructed classifier is the closet point to [0.5, 1., 1.5] by using the following python script −

print(neigh.kneighbors([[.5, 1., 1.5]])

Output

(array([[1.7]]), array([[1]], dtype = int64))

One-Class SVM

The One-Class SVM, introduced by Schölkopf et al., is the unsupervised Outlier Detection. It is also very efficient in high-dimensional data and estimates the support of a high-dimensional distribution. It is implemented in the Support Vector Machines module in the Sklearn.svm.OneClassSVM object. For defining a frontier, it requires a kernel (mostly used is RBF) and a scalar parameter.

For better understanding let's fit our data with svm.OneClassSVM object −

Example

from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)

Now, we can get the score_samples for input data as follows −

OSVMclf.score_samples(X)

Output

array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])

This chapter will help you in understanding the nearest neighbor methods in Sklearn.

Neighbor based learning method are of both types namely supervised and unsupervised. Supervised neighbors-based learning can be used for both classification as well as regression predictive problems but, it is mainly used for classification predictive problems in industry.

Neighbors based learning methods do not have a specialised training phase and uses all the data for training while classification. It also does not assume anything about the underlying data. That’s the reason they are lazy and non-parametric in nature.

The main principle behind nearest neighbor methods is −

• To find a predefined number of training samples closet in distance to the new data point

• Predict the label from these number of training samples.

Here, the number of samples can be a user-defined constant like in K-nearest neighbor learning or vary based on the local density of point like in radius-based neighbor learning.

sklearn.neighbors Module

Scikit-learn have sklearn.neighbors module that provides functionality for both unsupervised and supervised neighbors-based learning methods. As input, the classes in this module can handle either NumPy arrays or scipy.sparse matrices.

Types of algorithms

Different types of algorithms which can be used in neighbor-based methods’ implementation are as follows −

Brute Force

The brute-force computation of distances between all pairs of points in the dataset provides the most naïve neighbor search implementation. Mathematically, for N samples in D dimensions, brute-force approach scales as 0[DN²]

For small data samples, this algorithm can be very useful, but it becomes infeasible as and when number of samples grows. Brute force neighbor search can be enabled by writing the keyword algorithm=’brute’.

K-D Tree

One of the tree-based data structures that have been invented to address the computational inefficiencies of the brute-force approach, is KD tree data structure. Basically, the KD tree is a binary tree structure which is called K-dimensional tree. It recursively partitions the parameters space along the data axes by dividing it into nested orthographic regions into which the data points are filled.

Advantages

Following are some advantages of K-D tree algorithm −

Construction is fast − As the partitioning is performed only along the data axes, K-D tree’s construction is very fast.

Less distance computations − This algorithm takes very less distance computations to determine the nearest neighbor of a query point. It only takes [ ()] distance computations.

Disadvantages

Fast for only low-dimensional neighbor searches − It is very fast for low-dimensional (D < 20) neighbor searches but as and when D grow it becomes inefficient. As the partitioning is performed only along the data axes,

K-D tree neighbor searches can be enabled by writing the keyword algorithm=’kd_tree’.

Ball Tree

As we know that KD Tree is inefficient in higher dimensions, hence, to address this inefficiency of KD Tree, Ball tree data structure was developed. Mathematically, it recursively divides the data, into nodes defined by a centroid C and radius r, in such a way that each point in the node lies within the hyper-sphere defined by centroid C and radius r. It uses triangle inequality, given below, which reduces the number of candidate points for a neighbor search

$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$

Advantages

Following are some advantages of Ball Tree algorithm −

Efficient on highly structured data − As ball tree partition the data in a series of nesting hyper-spheres, it is efficient on highly structured data.

Out-performs KD-tree − Ball tree out-performs KD tree in high dimensions because it has spherical geometry of the ball tree nodes.

Disadvantages

Costly − Partition the data in a series of nesting hyper-spheres makes its construction very costly.

Ball tree neighbor searches can be enabled by writing the keyword algorithm=’ball_tree’.

Choosing Nearest Neighbors Algorithm

The choice of an optimal algorithm for a given dataset depends upon the following factors −

Number of samples (N) and Dimensionality (D)

These are the most important factors to be considered while choosing Nearest Neighbor algorithm. It is because of the reasons given below −

• The query time of Brute Force algorithm grows as O[DN].

• The query time of Ball tree algorithm grows as O[D log(N)].

• The query time of KD tree algorithm changes with D in a strange manner that is very difficult to characterize. When D < 20, the cost is O[D log(N)] and this algorithm is very efficient. On the other hand, it is inefficient in case when D > 20 because the cost increases to nearly O[DN].

Структура данных

Еще одним фактором, влияющим на производительность этих алгоритмов, является внутренняя размерность данных или их разреженность. Это потому, что это может сильно влиять на время запроса алгоритмов дерева Болла и дерева КД. В то время как время запроса алгоритма грубой силы не зависит от структуры данных. Как правило, алгоритмы Ball tree и KD tree обеспечивают более быстрое время запроса при внедрении в более разреженные данные с меньшей внутренней размерностью.

Количество соседей (k)

Количество соседей (k), запрошенных для точки запроса, влияет на время запроса алгоритмов дерева Болла и дерева KD. Время их запроса сокращается по мере увеличения числа соседей (k). В то время как время запроса грубой силы не зависит от значения k.

Количество точек запроса

Поскольку им требуется фаза построения, алгоритмы KD-дерева и Ball tree будут эффективны при большом количестве точек запроса. С другой стороны, при меньшем количестве точек запроса алгоритм грубой силы работает лучше, чем алгоритмы дерева КД и дерева Болла.

k-NN (k-Nearest Neighbor), один из простейших алгоритмов машинного обучения, непараметрический и ленивый по своей природе. Непараметрический означает, что нет никаких допущений для базового распределения данных, т.е. структура модели определяется на основе набора данных. Ленивое обучение или обучение на основе экземпляров означает, что для создания модели не требуются какие-либо обучающие данные, а на этапе тестирования используются все обучающие данные.

Алгоритм k-NN состоит из следующих двух шагов -

Шаг 1

На этом этапе он вычисляет и сохраняет k ближайших соседей для каждой выборки в обучающем наборе.

Шаг 2

На этом этапе для немаркированного образца он извлекает k ближайших соседей из набора данных. Затем среди этих k-ближайших соседей он прогнозирует класс посредством голосования (класс с большинством голосов побеждает).

Модуль, sklearn.neighbors который реализует алгоритм k-ближайших соседей, обеспечивает функциональность для unsupervised так же как supervised методы обучения на основе соседей.

Неконтролируемые ближайшие соседи реализуют различные алгоритмы (BallTree, KDTree или Brute Force), чтобы найти ближайшего соседа (ов) для каждой выборки. Эта неконтролируемая версия - это, по сути, только шаг 1, который обсуждался выше, и основа многих алгоритмов (KNN и K-средство является известным), которые требуют поиска соседей. Проще говоря, это неконтролируемый ученик для реализации поиска соседей.

С другой стороны, обучение на основе контролируемых соседей используется как для классификации, так и для регрессии.

Неконтролируемое обучение KNN

Как уже говорилось, существует множество алгоритмов, таких как KNN и K-Means, которые требуют поиска ближайшего соседа. Вот почему Scikit-learn решил реализовать часть поиска соседей как своего собственного «ученика». Причина, по которой поиск соседей выполняется в качестве отдельного ученика, заключается в том, что вычисление всего попарного расстояния для поиска ближайшего соседа, очевидно, не очень эффективно. Давайте посмотрим на модуль, используемый Sklearn для реализации обучения ближайшего соседа без учителя, вместе с примером.

Модуль Scikit-learn

sklearn.neighbors.NearestNeighborsэто модуль, используемый для реализации обучения ближайшего соседа без учителя. Он использует определенные алгоритмы ближайшего соседа с именами BallTree, KDTree или Brute Force. Другими словами, он действует как единый интерфейс для этих трех алгоритмов.

Параметры

В следующей таблице представлены параметры, используемые NearestNeighbors модуль -

Старший Нет	Параметр и описание
1	n_neighbors - int, необязательно Количество соседей. Значение по умолчанию - 5.
2	radius - поплавок, необязательно Это ограничивает расстояние от соседей до возвратов. Значение по умолчанию - 1.0.
3	algorithm - {'auto', 'ball_tree', 'kd_tree', 'brute'}, необязательно Этот параметр будет принимать алгоритм (BallTree, KDTree или Brute-force), который вы хотите использовать для вычисления ближайших соседей. Если вы укажете «auto», он попытается выбрать наиболее подходящий алгоритм на основе значений, переданных методу fit.
4	leaf_size - int, необязательно Это может повлиять на скорость построения и запроса, а также на объем памяти, необходимый для хранения дерева. Он передается в BallTree или KDTree. Хотя оптимальное значение зависит от характера проблемы, по умолчанию оно равно 30.
5	metric - строка или вызываемый Это метрика, используемая для вычисления расстояния между точками. Мы можем передать его как строку или вызываемую функцию. В случае вызываемой функции метрика вызывается для каждой пары строк, и результирующее значение записывается. Это менее эффективно, чем передача имени метрики в виде строки. Мы можем выбрать метрику из scikit-learn или scipy.spatial.distance. допустимые значения следующие - Scikit-learn - ['косинус', 'манхэттен', 'евклидово', 'l1', 'l2', 'cityblock'] Scipy.spatial.distance - ['braycurtis', 'canberra', 'chebyshev', 'dice', 'hamming', 'jaccard', 'корреляция', 'kulsinski', 'mahalanobis', 'minkowski', 'rogerstanimoto', 'russellrao', ' sokalmicheme »,« sokalsneath »,« seuclidean »,« sqeuclidean »,« yule »]. Метрика по умолчанию - «Минковский».
6	P - целое число, необязательно Это параметр для метрики Минковского. Значение по умолчанию - 2, что эквивалентно использованию Euclidean_distance (l2).
7	metric_params - dict, необязательно Это дополнительные аргументы ключевого слова для метрической функции. Значение по умолчанию - Нет.
8	N_jobs - int или None, необязательно Он повторно задает количество параллельных заданий, запускаемых для поиска соседей. Значение по умолчанию - Нет.

Implementation Example

В приведенном ниже примере будут найдены ближайшие соседи между двумя наборами данных с помощью sklearn.neighbors.NearestNeighbors модуль.

Во-первых, нам нужно импортировать необходимый модуль и пакеты -

from sklearn.neighbors import NearestNeighbors
import numpy as np

Теперь, после импорта пакетов, определите наборы данных между ними, которые мы хотим найти ближайших соседей -

Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])

Затем примените алгоритм обучения без учителя следующим образом:

nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')

Затем подгоните модель с набором входных данных.

nrst_neigh.fit(Input_data)

Теперь найдите K-соседей набора данных. Он вернет индексы и расстояния до соседей каждой точки.

distances, indices = nbrs.kneighbors(Input_data)
indices

Output

array(
   [
      [0, 1, 3],
      [1, 2, 0],
      [2, 1, 0],
      [3, 4, 0],
      [4, 5, 3],
      [5, 6, 4],
      [6, 5, 4]
   ], dtype = int64
)
distances

Output

array(
   [
      [0. , 1.41421356, 2.23606798],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 2.82842712],
      [0. , 1.41421356, 2.23606798],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 1.41421356],
      [0. , 1.41421356, 2.82842712]
   ]
)

Приведенный выше вывод показывает, что ближайший сосед каждой точки - это сама точка, т.е. в нуле. Это потому, что набор запросов соответствует обучающему набору.

Example

Мы также можем показать связь между соседними точками, создав разреженный граф следующим образом:

nrst_neigh.kneighbors_graph(Input_data).toarray()

Output

array(
   [
      [1., 1., 0., 1., 0., 0., 0.],
      [1., 1., 1., 0., 0., 0., 0.],
      [1., 1., 1., 0., 0., 0., 0.],
      [1., 0., 0., 1., 1., 0., 0.],
      [0., 0., 0., 1., 1., 1., 0.],
      [0., 0., 0., 0., 1., 1., 1.],
      [0., 0., 0., 0., 1., 1., 1.]
   ]
)

Как только мы подгоним без присмотра NearestNeighbors модели, данные будут храниться в структуре данных на основе значения, установленного для аргумента ‘algorithm’. После этого мы можем использовать этот неконтролируемый ученикkneighbors в модели, которая требует поиска соседей.

Complete working/executable program

from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()

Обучение KNN с учителем

Обучение на основе контролируемых соседей используется для следующих целей:

• Классификация для данных с дискретными метками
• Регрессия для данных с непрерывными метками.

Классификатор ближайшего соседа

Мы можем понять классификацию на основе соседей с помощью следующих двух характеристик:

• Он рассчитывается простым большинством голосов ближайших соседей каждой точки.
• Он просто хранит экземпляры обучающих данных, поэтому является типом необобщающего обучения.

Модули Scikit-learn

Ниже приведены два разных типа классификаторов ближайшего соседа, используемые scikit-learn.

S.No.	Классификаторы и описание
1.	KNeighborsClassifier K в имени этого классификатора представляет k ближайших соседей, где k - целочисленное значение, указанное пользователем. Следовательно, как следует из названия, этот классификатор реализует обучение на основе k ближайших соседей. Выбор значения k зависит от данных.
2.	РадиусСоседиКлассификатор Радиус в имени этого классификатора представляет ближайших соседей в пределах указанного радиуса r, где r - значение с плавающей запятой, указанное пользователем. Следовательно, как следует из названия, этот классификатор реализует обучение на основе числа соседей в пределах фиксированного радиуса r каждой точки обучения.

Регрессор ближайшего соседа

Он используется в тех случаях, когда метки данных носят непрерывный характер. Присвоенные метки данных вычисляются на основе среднего значения меток ближайших соседей.

Ниже приведены два разных типа регрессоров ближайшего соседа, используемые scikit-learn.

KNeighborsRegressor

K в имени этого регрессора представляет k ближайших соседей, где k является integer valueуказывается пользователем. Следовательно, как следует из названия, этот регрессор реализует обучение на основе k ближайших соседей. Выбор значения k зависит от данных. Давайте разберемся с этим подробнее на примере реализации.

Ниже приведены два разных типа регрессоров ближайшего соседа, используемые scikit-learn.

Пример реализации

В этом примере мы будем реализовывать KNN на наборе данных с именем Набор данных Iris Flower с помощью scikit-learn. KNeighborsRegressor.

Сначала импортируйте набор данных радужки следующим образом:

from sklearn.datasets import load_iris
iris = load_iris()

Теперь нам нужно разделить данные на данные для обучения и тестирования. Мы будем использовать Sklearntrain_test_split функция для разделения данных на соотношение 70 (данные обучения) и 20 (данные тестирования) -

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)

Далее мы будем выполнять масштабирование данных с помощью модуля предварительной обработки Sklearn следующим образом:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

Затем импортируйте KNeighborsRegressor class из Sklearn и укажите значение соседей следующим образом.

пример

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)

Вывод

KNeighborsRegressor(
   algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
   metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
   weights = 'uniform'
)

пример

Теперь мы можем найти MSE (среднеквадратичную ошибку) следующим образом:

print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))

Вывод

The MSE is: 4.4333349609375

пример

Теперь используйте его, чтобы предсказать значение следующим образом:

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))

Вывод

[0.66666667]

Полная рабочая / исполняемая программа

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()

scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)

print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))

RadiusNeighborsRegressor

Радиус в имени этого регрессора представляет ближайших соседей в пределах указанного радиуса r, где r - значение с плавающей запятой, указанное пользователем. Следовательно, как следует из названия, этот регрессор реализует обучение на основе числа соседей в пределах фиксированного радиуса r каждой обучающей точки. Давайте разберемся с этим подробнее с помощью примера реализации -

Пример реализации

В этом примере мы будем реализовывать KNN на наборе данных с именем Набор данных Iris Flower с помощью scikit-learn. RadiusNeighborsRegressor -

Сначала импортируйте набор данных радужки следующим образом:

from sklearn.datasets import load_iris
iris = load_iris()

Теперь нам нужно разделить данные на данные для обучения и тестирования. Мы будем использовать функцию Sklearn train_test_split, чтобы разделить данные на соотношение 70 (данные обучения) и 20 (данные тестирования) -

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)

Далее мы будем выполнять масштабирование данных с помощью модуля предварительной обработки Sklearn следующим образом:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

Затем импортируйте RadiusneighborsRegressor класс из Sklearn и укажите значение радиуса следующим образом:

import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)

пример

Теперь мы можем найти MSE (среднеквадратичную ошибку) следующим образом:

print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))

Вывод

The MSE is: The MSE is: 5.666666666666667

пример

Теперь используйте его, чтобы предсказать значение следующим образом:

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))

Вывод

[1.]

Полная рабочая / исполняемая программа

from sklearn.datasets import load_iris

iris = load_iris()

X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))

Наивные методы Байеса представляют собой набор алгоритмов контролируемого обучения, основанных на применении теоремы Байеса с сильным предположением, что все предикторы независимы друг от друга, т.е. наличие признака в классе не зависит от присутствия любой другой особенности в том же самом. класс. Это наивное предположение, поэтому эти методы называются наивными байесовскими методами.

Теорема Байеса утверждает следующее соотношение, чтобы найти апостериорную вероятность класса, то есть вероятность метки и некоторых наблюдаемых характеристик, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.

$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$

Вот, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ - апостериорная вероятность класса.

$P\left(\begin{array}{c} Y\end{array}\right)$ - априорная вероятность класса.

$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ - это вероятность, которая представляет собой вероятность предиктора данного класса.

$P\left(\begin{array}{c} features\end{array}\right)$ - априорная вероятность предсказателя.

Scikit-learn предоставляет различные модели наивных байесовских классификаторов, а именно гауссовский, полиномиальный, дополнительный и Бернулли. Все они различаются главным образом предположениями, которые они делают относительно распределения$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ т.е. вероятность предиктора данного класса.

Старший Нет	Модель и описание
1	Гауссовский наивный байесовский Гауссовский Наивный байесовский классификатор предполагает, что данные каждой метки взяты из простого гауссовского распределения.
2	Полиномиальный наивный байесовский Предполагается, что признаки взяты из простого полиномиального распределения.
3	Бернулли Наив Байес В этой модели предполагается, что функции двоичны (нули и единицы) по своей природе. Применение наивной байесовской классификации Бернулли - это классификация текста с моделью «мешка слов».
4	Дополнение наивного Байеса Он был разработан для исправления серьезных предположений, сделанных полиномиальным байесовским классификатором. Такой классификатор NB подходит для несбалансированных наборов данных.

Построение наивного байесовского классификатора

Мы также можем применить наивный байесовский классификатор к набору данных Scikit-learn. В приведенном ниже примере мы применяем GaussianNB и подбираем набор данных груди_cancer Scikit-leran.

пример

Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
   print(label_names)
   print(labels[0])
   print(feature_names[0])
   print(features[0])
train, test, train_labels, test_labels = train_test_split(
   features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)

Вывод

[
   1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
   1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 
   1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 
   1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 
   1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 
   0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 
   1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 
   1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 
   1 1 1 1 0 1 0 0 1 1 0 1
]

Приведенный выше результат состоит из серии нулей и единиц, которые в основном являются предсказанными значениями для классов опухолей, а именно злокачественных и доброкачественных.

В этой главе мы узнаем о методе обучения в Sklearn, который называется деревьями решений.

Решения tress (DT) - самый мощный непараметрический контролируемый метод обучения. Их можно использовать для задач классификации и регрессии. Основная цель DT - создать модель, предсказывающую значение целевой переменной, путем изучения простых правил принятия решений, выведенных из характеристик данных. Деревья решений имеют две основные сущности; один - корневой узел, на котором данные разделяются, а другой - узлы или листья принятия решений, на которых мы получили окончательный результат.

Алгоритмы дерева решений

Различные алгоритмы дерева решений объясняются ниже -

ID3

Он был разработан Россом Куинланом в 1986 году. Его также называют итеративным дихотомизатором 3. Основная цель этого алгоритма - найти те категориальные особенности для каждого узла, которые дадут наибольший информационный выигрыш для категориальных целей.

Он позволяет вырастить дерево до максимального размера, а затем, чтобы улучшить способность дерева работать с невидимыми данными, применяет этап сокращения. Результатом этого алгоритма будет многостороннее дерево.

C4.5

Это преемник ID3 и динамически определяет дискретный атрибут, который разбивает непрерывное значение атрибута на дискретный набор интервалов. По этой причине было снято ограничение категориальных функций. Он преобразует обученное дерево ID3 в наборы правил IF-THEN.

Чтобы определить последовательность, в которой должны применяться эти правила, в первую очередь оценивается точность каждого правила.

C5.0

Он работает аналогично C4.5, но использует меньше памяти и создает меньшие наборы правил. Он точнее, чем C4.5.

КОРЗИНА

Он называется алгоритмом деревьев классификации и регрессии. Он в основном генерирует двоичное разбиение, используя функции и пороговые значения, дающие наибольший прирост информации в каждом узле (так называемый индекс Джини).

Однородность зависит от индекса Джини, чем выше значение индекса Джини, тем выше будет однородность. Он похож на алгоритм C4.5, но разница в том, что он не вычисляет наборы правил и не поддерживает числовые целевые переменные (регрессию).

Классификация с деревьями решений

В этом случае переменные решения категоричны.

Sklearn Module - Библиотека Scikit-learn предоставляет имя модуля DecisionTreeClassifier для выполнения многоклассовой классификации набора данных.

Параметры

В следующей таблице представлены параметры, используемые sklearn.tree.DecisionTreeClassifier модуль -

Старший Нет	Параметр и описание
1	criterion - строка, необязательно по умолчанию = «gini» Он представляет функцию измерения качества разделения. Поддерживаемые критерии: «Джини» и «энтропия». По умолчанию используется значение Джини для примеси Джини, а энтропия - для получения информации.
2	splitter - строка, необязательно по умолчанию = «лучший» Он сообщает модели, какую стратегию из «лучшей» или «случайной» выбрать для разделения на каждом узле.
3	max_depth - int или None, необязательно по умолчанию = None Этот параметр определяет максимальную глубину дерева. Значение по умолчанию - None, что означает, что узлы будут расширяться до тех пор, пока все листья не станут чистыми или пока все листья не будут содержать менее min_smaples_split образцов.
4	min_samples_split - int, float, необязательно по умолчанию = 2 Этот параметр обеспечивает минимальное количество выборок, необходимое для разделения внутреннего узла.
5	min_samples_leaf - int, float, необязательно по умолчанию = 1 Этот параметр обеспечивает минимальное количество выборок, необходимое для конечного узла.
6	min_weight_fraction_leaf - float, необязательно по умолчанию = 0. С этим параметром модель получит минимальную взвешенную долю от суммы весов, которая должна быть в листовом узле.
7	max_features - int, float, string или None, необязательно по умолчанию = None Это дает модели количество функций, которые необходимо учитывать при поиске наилучшего разделения.
8	random_state - int, экземпляр RandomState или None, необязательно, по умолчанию = none Этот параметр представляет собой начальное число сгенерированного псевдослучайного числа, которое используется при перетасовке данных. Следующие варианты - int- В этом случае random_state - это начальное число, используемое генератором случайных чисел. RandomState instance - В этом случае random_state - это генератор случайных чисел. None - В этом случае генератор случайных чисел - это экземпляр RandonState, используемый np.random.
9	max_leaf_nodes - int или None, необязательно по умолчанию = None Этот параметр позволит вырастить дерево с max_leaf_nodes способом «лучший первый». Значение по умолчанию - none, что означает неограниченное количество конечных узлов.
10	min_impurity_decrease - float, необязательно по умолчанию = 0. Это значение работает как критерий для разделения узла, поскольку модель разделит узел, если это разделение вызовет уменьшение примеси больше или равное min_impurity_decrease value.
11	min_impurity_split - float, по умолчанию = 1e-7 Он представляет собой порог для ранней остановки роста деревьев.
12	class_weight - dict, список dicts, «сбалансированный» или None, по умолчанию = None Он представляет собой веса, связанные с классами. Форма: {class_label: weight}. Если мы используем вариант по умолчанию, это означает, что все классы должны иметь единичный вес. С другой стороны, если вы выберетеclass_weight: balanced, он будет использовать значения y для автоматической настройки весов.
13	presort - bool, необязательно по умолчанию = False Он сообщает модели, следует ли предварительно отсортировать данные, чтобы ускорить поиск наиболее подходящих разбиений. Значение по умолчанию - false, но если установлено значение true, это может замедлить процесс обучения.

Атрибуты

В следующей таблице представлены атрибуты, используемые sklearn.tree.DecisionTreeClassifier модуль -

Старший Нет	Параметр и описание
1	feature_importances_ - массив формы = [n_features] Этот атрибут вернет важность функции.
2	classes_: - массив shape = [n_classes] или список таких массивов Он представляет собой метки классов, то есть проблему с одним выходом, или список массивов меток классов, то есть проблему с несколькими выходами.
3	max_features_ - int Он представляет собой выведенное значение параметра max_features.
4	n_classes_ - int или список Он представляет количество классов, то есть задачу с одним выходом, или список количества классов для каждого выхода, то есть задачу с несколькими выходами.
5	n_features_ - int Это дает количество features когда выполняется метод fit ().
6	n_outputs_ - int Это дает количество outputs когда выполняется метод fit ().

Методы

В следующей таблице представлены методы, используемые sklearn.tree.DecisionTreeClassifier модуль -

Старший Нет	Параметр и описание
1	apply(self, X [, check_input]) Этот метод вернет индекс листа.
2	decision_path(self, X [, check_input]) Как следует из названия, этот метод вернет путь решения в дереве
3	fit(self, X, y [, sample_weight,…]) Метод fit () построит классификатор дерева решений из заданного обучающего набора (X, y).
4	get_depth(сам) Как следует из названия, этот метод вернет глубину дерева решений.
5	get_n_leaves(сам) Как следует из названия, этот метод вернет количество листьев дерева решений.
6	get_params(сам [, глубоко]) Мы можем использовать этот метод для получения параметров для оценки.
7	predict(self, X [, check_input]) Он предскажет значение класса для X.
8	predict_log_proba(я, X) Он будет предсказывать логарифмические вероятности классов предоставленных нами входных выборок X.
9	predict_proba(self, X [, check_input]) Он будет предсказывать вероятности классов предоставленных нами входных выборок X.
10	score(self, X, y [, sample_weight]) Как следует из названия, метод score () возвращает среднюю точность для заданных тестовых данных и меток.
11	set_params(сам, \ * \ * параметры) С помощью этого метода мы можем установить параметры оценщика.

Пример реализации

Скрипт Python ниже будет использовать sklearn.tree.DecisionTreeClassifier модуль для создания классификатора для прогнозирования мужского или женского пола из нашего набора данных, содержащего 25 образцов и две характеристики, а именно «рост» и «длину волос» -

from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)

Вывод

['Woman']

Мы также можем предсказать вероятность каждого класса, используя следующий метод python pred_proba () следующим образом:

пример

prediction = DTclf.predict_proba([[135,29]])
print(prediction)

Вывод

[[0. 1.]]

Регрессия с деревьями решений

В этом случае переменные решения непрерывны.

Sklearn Module - Библиотека Scikit-learn предоставляет имя модуля DecisionTreeRegressor для применения деревьев решений к задачам регрессии.

Параметры

Параметры, используемые DecisionTreeRegressor почти такие же, как использовались в DecisionTreeClassifierмодуль. Отличие заключается в параметре «критерий». ЗаDecisionTreeRegressor модули ‘criterion: строка, необязательный параметр default = «mse» 'имеет следующие значения -

• mse- Это означает среднеквадратичную ошибку. Это равносильно уменьшению дисперсии как критерию выбора функции. Это минимизирует потери L2, используя среднее значение каждого конечного узла.

• freidman_mse - Он также использует среднеквадратичную ошибку, но с оценкой улучшения Фридмана.

• mae- Это средняя абсолютная ошибка. Он сводит к минимуму потери L1, используя медианное значение каждого конечного узла.

Другое отличие в том, что в нем нет ‘class_weight’ параметр.

Атрибуты

Атрибуты DecisionTreeRegressor также такие же, как у DecisionTreeClassifierмодуль. Разница в том, что в нем нет‘classes_’ и ‘n_classes_'атрибуты.

Методы

Методы DecisionTreeRegressor также такие же, как у DecisionTreeClassifierмодуль. Разница в том, что в нем нет‘predict_log_proba()’ и ‘predict_proba()’'атрибуты.

Пример реализации

Метод fit () в регрессионной модели дерева решений принимает значения y с плавающей запятой. давайте посмотрим на простой пример реализации, используяSklearn.tree.DecisionTreeRegressor -

from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)

После установки мы можем использовать эту регрессионную модель, чтобы сделать прогноз следующим образом:

DTreg.predict([[4, 5]])

Вывод

array([1.5])

Эта глава поможет вам понять рандомизированные деревья решений в Sklearn.

Алгоритмы рандомизированного дерева решений

Поскольку мы знаем, что DT обычно обучается путем рекурсивного разделения данных, но, будучи склонным к переобучению, они были преобразованы в случайные леса путем обучения многих деревьев на различных подвыборках данных. Вsklearn.ensemble модуль имеет следующие два алгоритма, основанные на рандомизированных деревьях решений -

Алгоритм случайного леса

Для каждого рассматриваемого объекта вычисляется локально оптимальная комбинация признака / разделения. В случайном лесу каждое дерево решений в ансамбле строится из выборки, взятой с заменой из обучающего набора, затем получает прогноз от каждого из них и, наконец, выбирает лучшее решение посредством голосования. Его можно использовать как для классификации, так и для задач регрессии.

Классификация со случайным лесом

Для создания классификатора случайного леса модуль Scikit-learn предоставляет sklearn.ensemble.RandomForestClassifier. При построении классификатора случайного леса основными параметрами, которые использует этот модуль, являются:‘max_features’ и ‘n_estimators’.

Вот, ‘max_features’- это размер случайных подмножеств функций, которые следует учитывать при разделении узла. Если мы выберем для этого параметра значение «Нет», тогда будут учитываться все функции, а не случайное подмножество. С другой стороны,n_estimatorsколичество деревьев в лесу. Чем больше будет деревьев, тем лучше будет результат. Но это также займет больше времени.

Пример реализации

В следующем примере мы создаем классификатор случайного леса, используя sklearn.ensemble.RandomForestClassifier а также проверка его точности с помощью cross_val_score модуль.

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()

Вывод

0.9997

пример

Мы также можем использовать набор данных sklearn для создания классификатора случайного леса. Как и в следующем примере, мы используем набор данных радужной оболочки глаза. Мы также найдем его оценку точности и матрицу неточностей.

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)

Вывод

Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
                  precision recall f1-score support
Iris-setosa       1.00        1.00  1.00     14
Iris-versicolor   1.00        0.95  0.97     19
Iris-virginica    0.92        1.00  0.96     12

micro avg         0.98        0.98  0.98     45
macro avg         0.97        0.98  0.98     45
weighted avg      0.98        0.98  0.98     45

Accuracy: 0.9777777777777777

Регрессия со случайным лесом

Для создания случайной регрессии леса модуль Scikit-learn предоставляет sklearn.ensemble.RandomForestRegressor. При построении случайного регрессора леса он будет использовать те же параметры, что иsklearn.ensemble.RandomForestClassifier.

Пример реализации

В следующем примере мы создаем случайный регрессор леса, используя sklearn.ensemble.RandomForestregressor а также прогнозирование новых значений с помощью метода pred ().

from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)

Вывод

RandomForestRegressor(
   bootstrap = True, criterion = 'mse', max_depth = 10,
   max_features = 'auto', max_leaf_nodes = None,
   min_impurity_decrease = 0.0, min_impurity_split = None,
   min_samples_leaf = 1, min_samples_split = 2,
   min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
   oob_score = False, random_state = 0, verbose = 0, warm_start = False
)

После установки мы можем предсказать из регрессионной модели следующим образом:

print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

Вывод

[98.47729198]

Методы Extra-Tree

Для каждой рассматриваемой функции он выбирает случайное значение для разделения. Преимущество использования дополнительных методов дерева заключается в том, что это позволяет немного уменьшить дисперсию модели. Недостатком использования этих методов является то, что они немного увеличивают смещение.

Классификация методом экстра-дерева

Для создания классификатора с использованием метода Extra-tree модуль Scikit-learn предоставляет sklearn.ensemble.ExtraTreesClassifier. Он использует те же параметры, что иsklearn.ensemble.RandomForestClassifier. Единственная разница в том, как они строят деревья, как описано выше.

Пример реализации

В следующем примере мы создаем классификатор случайного леса, используя sklearn.ensemble.ExtraTreeClassifier а также проверка его точности с помощью cross_val_score модуль.

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()

Вывод

1.0

пример

Мы также можем использовать набор данных sklearn для создания классификатора с использованием метода Extra-Tree. Как и в следующем примере, мы используем набор данных Pima-Indian.

from pandas import read_csv

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())

Вывод

0.7551435406698566

Регрессия с использованием метода экстра-дерева

Для создания Extra-Tree регрессии, модуль Scikit-learn предоставляет sklearn.ensemble.ExtraTreesRegressor. При построении случайного регрессора леса он будет использовать те же параметры, что иsklearn.ensemble.ExtraTreesClassifier.

Пример реализации

В следующем примере мы применяем sklearn.ensemble.ExtraTreesregressorи на тех же данных, которые мы использовали при создании случайного регрессора леса. Давайте посмотрим на разницу в выводе

from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)

Вывод

ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
   max_features = 'auto', max_leaf_nodes = None,
   min_impurity_decrease = 0.0, min_impurity_split = None,
   min_samples_leaf = 1, min_samples_split = 2,
   min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
   oob_score = False, random_state = 0, verbose = 0, warm_start = False)

пример

После установки мы можем предсказать из регрессионной модели следующим образом:

print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

Вывод

[85.50955817]

В этой главе мы узнаем о методах повышения в Sklearn, которые позволяют построить ансамблевую модель.

Методы повышения строят ансамблевую модель поэтапно. Главный принцип состоит в том, чтобы строить модель постепенно, последовательно обучая каждый оценщик базовой модели. Чтобы создать мощный ансамбль, эти методы в основном объединяют нескольких недельных учеников, которые последовательно обучаются на нескольких итерациях обучающих данных. В модуле sklearn.ensemble есть два метода повышения.

AdaBoost

Это один из наиболее успешных методов ансамбля повышения, главный ключ которого в том, как они присваивают веса экземплярам в наборе данных. Вот почему алгоритм должен уделять меньше внимания экземплярам при построении последующих моделей.

Классификация с AdaBoost

Для создания классификатора AdaBoost модуль Scikit-learn предоставляет sklearn.ensemble.AdaBoostClassifier. При построении этого классификатора основным параметром, используемым этим модулем, являетсяbase_estimator. Здесь base_estimator - это значениеbase estimatorиз которого строится усиленный ансамбль. Если мы выберем для этого параметра значение «Нет», то базовая оценка будетDecisionTreeClassifier(max_depth=1).

Пример реализации

В следующем примере мы создаем классификатор AdaBoost, используя sklearn.ensemble.AdaBoostClassifier а также прогнозирование и проверка своей оценки.

from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)

Вывод

AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)

пример

После установки мы можем прогнозировать новые значения следующим образом:

print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

Вывод

[1]

пример

Теперь мы можем проверить счет следующим образом -

ADBclf.score(X, y)

Вывод

0.995

пример

Мы также можем использовать набор данных sklearn для создания классификатора с использованием метода Extra-Tree. Например, в примере, приведенном ниже, мы используем набор данных Pima-Indian.

from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())

Вывод

0.7851435406698566

Регресс с AdaBoost

Для создания регрессора с помощью метода Ada Boost библиотека Scikit-learn предоставляет sklearn.ensemble.AdaBoostRegressor. При построении регрессора он будет использовать те же параметры, что иsklearn.ensemble.AdaBoostClassifier.

Пример реализации

В следующем примере мы создаем регрессор AdaBoost, используя sklearn.ensemble.AdaBoostregressor а также прогнозирование новых значений с помощью метода pred ().

from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)

Вывод

AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)

пример

После установки мы можем предсказать из регрессионной модели следующим образом:

print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))

Вывод

[85.50955817]

Повышение градиента дерева

Его еще называют Gradient Boosted Regression Trees(GRBT). По сути, это обобщение повышения до произвольных дифференцируемых функций потерь. Он создает модель прогнозирования в виде ансамбля моделей прогнозирования на неделю. Его можно использовать для задач регрессии и классификации. Их главное преимущество заключается в том, что они естественным образом обрабатывают данные смешанного типа.

Классификация с помощью Gradient Tree Boost

Для создания классификатора Gradient Tree Boost модуль Scikit-learn предоставляет sklearn.ensemble.GradientBoostingClassifier. При построении этого классификатора основным параметром, используемым этим модулем, является «убыток». Здесь «потеря» - это значение функции потерь, которое необходимо оптимизировать. Если мы выбираем потерю = отклонение, это относится к отклонению для классификации с вероятностными выходами.

С другой стороны, если мы выберем для этого параметра экспоненциальное значение, тогда он восстановит алгоритм AdaBoost. Параметрn_estimatorsбудет контролировать количество обучающихся в неделю. Гиперпараметр с именемlearning_rate (в диапазоне (0,0, 1,0]) будет контролировать переоснащение посредством усадки.

Пример реализации

В следующем примере мы создаем классификатор Gradient Boosting, используя sklearn.ensemble.GradientBoostingClassifier. Мы настраиваем этот классификатор на 50-недельных учеников.

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]

GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)

Вывод

0.8724285714285714

пример

Мы также можем использовать набор данных sklearn для создания классификатора с помощью Gradient Boosting Classifier. Как и в следующем примере, мы используем набор данных Pima-Indian.

from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())

Вывод

0.7946582356674234

Регрессия с помощью Gradient Tree Boost

Для создания регрессора с помощью метода Gradient Tree Boost библиотека Scikit-learn предоставляет sklearn.ensemble.GradientBoostingRegressor. Он может указать функцию потерь для регрессии через параметр name loss. Значение потерь по умолчанию - ls.

Пример реализации

В следующем примере мы создаем регрессор Gradient Boosting, используя sklearn.ensemble.GradientBoostingregressor а также нахождение среднеквадратичной ошибки с помощью метода mean_squared_error ().

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)

После подбора мы можем найти среднеквадратичную ошибку следующим образом:

mean_squared_error(y_test, GDBreg.predict(X_test))

Вывод

5.391246106657164

Здесь мы изучим методы кластеризации в Sklearn, которые помогут выявить какое-либо сходство в выборках данных.

Методы кластеризации - один из наиболее полезных методов машинного обучения без учителя, который используется для поиска шаблонов сходства и взаимосвязи между выборками данных. После этого они группируют эти образцы в группы, имеющие сходство на основе характеристик. Кластеризация определяет внутреннюю группировку среди имеющихся немаркированных данных, поэтому это важно.

Библиотека Scikit-learn имеет sklearn.clusterвыполнить кластеризацию немаркированных данных. В этом модуле scikit-leran имеют следующие методы кластеризации -

KMeans

Этот алгоритм вычисляет центроиды и выполняет итерацию, пока не найдет оптимальный центроид. Требуется указать количество кластеров, поэтому предполагается, что они уже известны. Основная логика этого алгоритма состоит в том, чтобы сгруппировать данные, разделяя выборки в n группах с равной дисперсией, минимизируя критерии, известные как инерция. Количество кластеров, идентифицированных алгоритмом, представлено буквой K.

Scikit-learn имеют sklearn.cluster.KMeansмодуль для выполнения кластеризации K-средних. При вычислении центров кластеров и значения инерции параметр с именемsample_weight позволяет sklearn.cluster.KMeans модуль для присвоения большего веса некоторым образцам.

Распространение сродства

Этот алгоритм основан на концепции «передачи сообщений» между разными парами выборок до схождения. Перед запуском алгоритма не требуется указывать количество кластеров. Алгоритм имеет временную сложность порядка (2), что является его самым большим недостатком.

Scikit-learn имеют sklearn.cluster.AffinityPropagation модуль для выполнения кластеризации Affinity Propagation.

Средний сдвиг

Этот алгоритм в основном обнаруживает blobsв гладкой плотности образцов. Он назначает точки данных кластерам итеративно, сдвигая точки в сторону максимальной плотности точек данных. Вместо того, чтобы полагаться на параметр с именемbandwidth диктуя размер области для поиска, она автоматически устанавливает количество кластеров.

Scikit-learn имеют sklearn.cluster.MeanShift модуль для выполнения кластеризации среднего сдвига.

Спектральная кластеризация

Перед кластеризацией этот алгоритм в основном использует собственные значения, то есть спектр матрицы подобия данных, для уменьшения размерности в меньшем количестве измерений. Использование этого алгоритма не рекомендуется при большом количестве кластеров.

Scikit-learn имеют sklearn.cluster.SpectralClustering модуль для выполнения спектральной кластеризации.

Иерархическая кластеризация

Этот алгоритм строит вложенные кластеры путем последовательного слияния или разделения кластеров. Эта кластерная иерархия представлена ​​в виде дендрограммы, то есть дерева. Он попадает в следующие две категории -

Agglomerative hierarchical algorithms- В этом виде иерархического алгоритма каждая точка данных обрабатывается как единый кластер. Затем он последовательно агломерирует пары кластеров. Здесь используется восходящий подход.

Divisive hierarchical algorithms- В этом иерархическом алгоритме все точки данных рассматриваются как один большой кластер. При этом процесс кластеризации включает в себя разделение одного большого кластера на несколько небольших кластеров с использованием нисходящего подхода.

Scikit-learn имеют sklearn.cluster.AgglomerativeClustering модуль для выполнения агломеративной иерархической кластеризации.

DBSCAN

Это означает “Density-based spatial clustering of applications with noise”. Этот алгоритм основан на интуитивном понятии «кластеры» и «шум», согласно которому кластеры представляют собой плотные области с меньшей плотностью в пространстве данных, разделенные областями с более низкой плотностью точек данных.

Scikit-learn имеют sklearn.cluster.DBSCANмодуль для выполнения кластеризации DBSCAN. Есть два важных параметра, а именно min_samples и eps, которые используются этим алгоритмом для определения плотности.

Более высокое значение параметра min_samples или меньшее значение параметра eps будет указывать на более высокую плотность точек данных, которая необходима для формирования кластера.

ОПТИКА

Это означает “Ordering points to identify the clustering structure”. Этот алгоритм также находит кластеры на основе плотности в пространственных данных. Его основная рабочая логика похожа на DBSCAN.

Он устраняет главную слабость алгоритма DBSCAN - проблему обнаружения значимых кластеров в данных различной плотности - путем упорядочивания точек в базе данных таким образом, что пространственно ближайшие точки становятся соседями в упорядочении.

Scikit-learn имеют sklearn.cluster.OPTICS модуль для выполнения кластеризации ОПТИКИ.

БЕРЕЗА

Это означает Сбалансированное итеративное сокращение и кластеризацию с использованием иерархий. Он используется для выполнения иерархической кластеризации больших наборов данных. Он строит дерево с именемCFT т.е. Characteristics Feature Tree, для приведенных данных.

Преимущество CFT состоит в том, что узлы данных, называемые узлами CF (Characteristics Feature), содержат необходимую информацию для кластеризации, что дополнительно исключает необходимость хранить все входные данные в памяти.

Scikit-learn имеют sklearn.cluster.Birch модуль для выполнения кластеризации БЕРЕЗЫ.

Сравнение алгоритмов кластеризации

В следующей таблице будет представлено сравнение (на основе параметров, масштабируемости и метрики) алгоритмов кластеризации в scikit-learn.

Старший Нет	Название алгоритма	Параметры	Масштабируемость	Используемая метрика
1	К-средние	Кол-во кластеров	Очень большие n_samples	Расстояние между точками.
2	Распространение сродства	Демпфирование	Это не масштабируется с помощью n_samples	График Расстояние
3	Средний сдвиг	Пропускная способность	Это не масштабируется с помощью n_samples.	Расстояние между точками.
4	Спектральная кластеризация	Кол-во кластеров	Средний уровень масштабируемости с n_samples. Небольшой уровень масштабируемости с n_clusters.	График Расстояние
5	Иерархическая кластеризация	Пороговое значение расстояния или количество кластеров	Большие n_samples Большие n_clusters	Расстояние между точками.
6	DBSCAN	Размер района	Очень большие n_samples и средние n_clusters.	Расстояние до ближайшей точки
7	ОПТИКА	Минимальное членство в кластере	Очень большие n_samples и большие n_clusters.	Расстояние между точками.
8	БЕРЕЗА	Порог, коэффициент ветвления	Большие n_samples Большие n_clusters	Евклидово расстояние между точками.

Кластеризация K-средних в наборе данных Scikit-learn Digit

В этом примере мы применим кластеризацию K-средних к набору данных цифр. Этот алгоритм идентифицирует похожие цифры без использования исходной информации на этикетке. Реализация выполняется на ноутбуке Jupyter.

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

Вывод

1797, 64)

Эти выходные данные показывают, что набор цифровых данных содержит 1797 образцов с 64 функциями.

пример

Теперь выполните кластеризацию K-средних следующим образом:

kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

Вывод

(10, 64)

Эти выходные данные показывают, что кластеризация K-средних создала 10 кластеров с 64 функциями.

пример

fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)

Вывод

В выходных данных ниже представлены изображения, показывающие центры кластеров, полученные с помощью кластеризации K-средних.

Затем скрипт Python ниже сопоставит изученные метки кластера (с помощью K-средних) с найденными в них истинными метками -

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]

Мы также можем проверить точность с помощью приведенной ниже команды.

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

Вывод

0.7935447968836951

Полный пример реализации

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
   axi.set(xticks=[], yticks = [])
   axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

Существуют различные функции, с помощью которых мы можем оценить производительность алгоритмов кластеризации.

Ниже приведены некоторые важные и наиболее часто используемые функции, данные Scikit-learn для оценки производительности кластеризации.

Скорректированный индекс ранда

Rand Index - это функция, которая вычисляет меру сходства между двумя кластерами. Для этого вычисления рандомный индекс рассматривает все пары выборок и счетные пары, которые назначены в одинаковые или разные кластеры в предсказанной и истинной кластеризации. После этого исходный балл Rand Index «скорректирован на случайность» в скорректированный рейтинг Rand Index с использованием следующей формулы:

$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$

Он имеет два параметра, а именно labels_true, который является метками класса наземной истины, и labels_pred, которые представляют собой метку кластера для оценки.

пример

from sklearn.metrics.cluster import adjusted_rand_score
   
   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

adjusted_rand_score(labels_true, labels_pred)

Вывод

0.4444444444444445

Идеальная маркировка будет иметь 1 балл, а плохая маркировка или независимая маркировка - 0 или отрицательный результат.

Оценка на основе взаимной информации

Взаимная информация - это функция, которая вычисляет согласование двух назначений. Он игнорирует перестановки. Доступны следующие версии -

Нормализованная взаимная информация (NMI)

Scikit учиться есть sklearn.metrics.normalized_mutual_info_score модуль.

пример

from sklearn.metrics.cluster import normalized_mutual_info_score
   
   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

normalized_mutual_info_score (labels_true, labels_pred)

Вывод

0.7611702597222881

Скорректированная взаимная информация (AMI)

Scikit учиться есть sklearn.metrics.adjusted_mutual_info_score модуль.

пример

from sklearn.metrics.cluster import adjusted_mutual_info_score

   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

adjusted_mutual_info_score (labels_true, labels_pred)

Вывод

0.4444444444444448

Оценка Фаулкса-Мэллоуса

Функция Фаулкса-Маллоуса измеряет сходство двух кластеризации набора точек. Его можно определить как среднее геометрическое для попарной точности и полноты.

Математически,

$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$

Вот, TP = True Positive - количество пар точек, принадлежащих одним и тем же кластерам как в истинных, так и в предсказанных метках.

FP = False Positive - количество пар точек, принадлежащих одним и тем же кластерам в истинных метках, но не в предсказанных метках.

FN = False Negative - количество пар точек, принадлежащих одним и тем же кластерам в предсказанных метках, но не в истинных метках.

В Scikit learn есть модуль sklearn.metrics.fowlkes_mallows_score -

пример

from sklearn.metrics.cluster import fowlkes_mallows_score

   labels_true = [0, 0, 1, 1, 1, 1]
   labels_pred = [0, 0, 2, 2, 3, 3]

fowlkes_mallows__score (labels_true, labels_pred)

Вывод

0.6546536707079771

Коэффициент силуэта

Функция Silhouette вычислит средний коэффициент силуэта для всех выборок, используя среднее расстояние внутри кластера и среднее расстояние до ближайшего кластера для каждого образца.

Математически,

$$S=\left(b-a\right)/max\left(a,b\right)$$

Здесь a - расстояние внутри кластера.

и, b - среднее расстояние до ближайшего кластера.

Scikit изучает sklearn.metrics.silhouette_score модуль -

пример

from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target

kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')

Вывод

0.5528190123564091

Матрица непредвиденных обстоятельств

Эта матрица сообщит мощность пересечения для каждой доверенной пары (истинная, предсказанная). Матрица неточностей для задач классификации представляет собой квадратную матрицу непредвиденных обстоятельств.

Scikit изучает sklearn.metrics.contingency_matrix модуль.

пример

from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)

Вывод

array([
   [0, 2, 1],
   [1, 1, 1]
])

Первая строка вышеприведенных выходных данных показывает, что среди трех выборок, истинный кластер которых равен «a», ни один из них не находится в 0, два из них находятся в 1, а 1 - в 2. С другой стороны, вторая строка показывает, что среди трех выборок чей истинный кластер - «b», 1 находится в 0, 1 находится в 1 и 1 находится в 2.

Снижение размерности, метод машинного обучения без учителя используется для уменьшения количества переменных функций для каждой выборки данных, выбирая набор основных функций. Анализ главных компонентов (PCA) - один из популярных алгоритмов уменьшения размерности.

Точный PCA

Principal Component Analysis (PCA) используется для уменьшения линейной размерности с помощью Singular Value Decomposition(SVD) данных, чтобы проецировать их в пространство более низкой размерности. При декомпозиции с использованием PCA входные данные центрируются, но не масштабируются для каждого объекта перед применением SVD.

Библиотека машинного обучения Scikit-learn предоставляет sklearn.decomposition.PCAмодуль, реализованный как объект-преобразователь, который изучает n компонентов в своем методе fit (). Его также можно использовать для новых данных, чтобы проецировать их на эти компоненты.

пример

В приведенном ниже примере будет использоваться модуль sklearn.decomposition.PCA для поиска 5 лучших основных компонентов из набора данных о диабете индейцев пима.

from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)

Вывод

Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
   [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
   [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
   [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
   [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
   [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]

Инкрементальный PCA

Incremental Principal Component Analysis (IPCA) используется для устранения самого большого ограничения анализа основных компонентов (PCA), то есть PCA поддерживает только пакетную обработку, что означает, что все входные данные, подлежащие обработке, должны умещаться в памяти.

Библиотека машинного обучения Scikit-learn предоставляет sklearn.decomposition.IPCA модуль, который позволяет реализовать Out-of-Core PCA либо с помощью своего partial_fit для последовательно извлеченных фрагментов данных или путем включения использования np.memmap, файл с отображением в память, без загрузки всего файла в память.

То же, что и PCA, при декомпозиции с использованием IPCA входные данные центрируются, но не масштабируются для каждой функции перед применением SVD.

пример

В приведенном ниже примере будет использоваться sklearn.decomposition.IPCA модуль на цифровом наборе данных Sklearn.

from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shape

Вывод

(1797, 10)

Здесь мы можем частично уместить меньшие пакеты данных (как мы делали 100 на пакет), или вы можете позволить fit() функция для разделения данных на партии.

Ядро PCA

Анализ основных компонентов ядра, расширение PCA, позволяет снизить нелинейную размерность с помощью ядер. Он поддерживает какtransform and inverse_transform.

Библиотека машинного обучения Scikit-learn предоставляет sklearn.decomposition.KernelPCA модуль.

пример

В приведенном ниже примере будет использоваться sklearn.decomposition.KernelPCAмодуль на цифровом наборе данных Sklearn. Мы используем сигмовидное ядро.

from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shape

Вывод

(1797, 10)

PCA с использованием рандомизированной SVD

Анализ главных компонентов (PCA) с использованием рандомизированного SVD используется для проецирования данных в пространство меньшей размерности с сохранением большей части дисперсии путем отбрасывания сингулярного вектора компонентов, связанных с более низкими сингулярными значениями. Здесьsklearn.decomposition.PCA модуль с необязательным параметром svd_solver=’randomized’ будет очень полезно.

пример

В приведенном ниже примере будет использоваться sklearn.decomposition.PCA модуль с необязательным параметром svd_solver = 'randomized', чтобы найти 7 лучших основных компонентов из набора данных о диабете индейцев пима.

from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)

Вывод

Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
   [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
   [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
   [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
   [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
   [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
   [-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
   [ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]